Proste 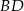 i
i 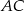 są równoległe. Długość odcinków
są równoległe. Długość odcinków 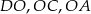 przedstawione są na rysunku. Wobec tego długość odcinka
przedstawione są na rysunku. Wobec tego długość odcinka 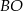 wynosi
wynosi
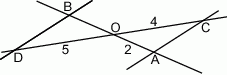
A) 10 B) 1,6 C) 2,5 D) 
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Proste 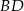 i
i 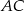 są równoległe. Długość odcinków
są równoległe. Długość odcinków 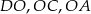 przedstawione są na rysunku. Wobec tego długość odcinka
przedstawione są na rysunku. Wobec tego długość odcinka 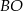 wynosi
wynosi

A) 10 B) 1,6 C) 2,5 D) 
Proste 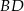 i
i 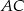 są równoległe. Długość odcinków
są równoległe. Długość odcinków 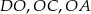 przedstawione są na rysunku. Wobec tego długość odcinka
przedstawione są na rysunku. Wobec tego długość odcinka 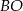 wynosi
wynosi
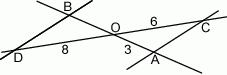
A) 16 B) 4 C) 2,5 D) 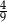
Na rysunku proste 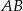 i
i 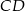 są równoległe. Odcinek
są równoległe. Odcinek 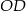 ma długość
ma długość
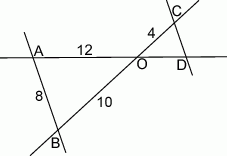
A) 3,2 B) 4,8 C) 3 D) 4
W trójkącie prostokątnym środkowa poprowadzona na przeciwprostokątną ma długość 4. Pole koła opisanego na tym trójkącie wynosi
A) 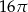 B)
B) 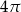 C)
C) 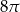 D)
D) 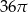
Środkowa w trójkącie prostokątnym poprowadzona z wierzchołka kąta prostego ma długość 1. Zatem pole koła opisanego na tym trójkącie wynosi
A) 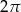 B)
B) 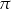 C)
C) 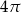 D)
D) 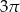
Kąty między bokiem trójkąta ostrokątnego a wysokościami opuszczonymi z należących do tego boku wierzchołków mają miary 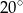 i
i 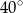 . Kąty tego trójkąta mają miary:
. Kąty tego trójkąta mają miary:
A) 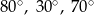 B)
B) 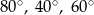 C)
C) 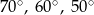 D)
D) 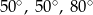
Kąty między bokiem trójkąta ostrokątnego a wysokościami opuszczonymi z należących do tego boku wierzchołków mają miary 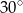 i
i 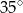 . Kąty tego trójkąta mają miary:
. Kąty tego trójkąta mają miary:
A) 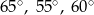 B)
B) 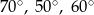 C)
C) 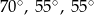 D)
D) 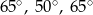
Cięciwa okręgu o promieniu 17 cm ma długość 30 cm. Odległość środka okręgu od tej cięciwy wynosi
A) 9 cm B) 13 cm C) 8 cm D) 15 cm
Odcinek 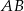 ma długość 24 cm i jest cięciwą okręgu o środku w punkcie
ma długość 24 cm i jest cięciwą okręgu o środku w punkcie 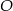 i średnicy długości 25 cm. Odległość punktu
i średnicy długości 25 cm. Odległość punktu 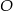 od cięciwy
od cięciwy 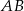 wynosi
wynosi
A) 3,5 cm B) 12 cm C) 6 cm D) 12,5 cm
Odcinek 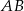 ma długość 20 cm i jest cięciwą okręgu o środku w punkcie
ma długość 20 cm i jest cięciwą okręgu o środku w punkcie 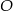 i średnicy długości 25 cm. Odległość punktu
i średnicy długości 25 cm. Odległość punktu 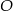 od cięciwy
od cięciwy 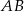 wynosi
wynosi
A) 12 cm B) 7,5 cm C) 6 cm D) 4,5 cm
Odcinek 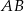 ma długość 12 cm i jest cięciwą okręgu o środku w punkcie
ma długość 12 cm i jest cięciwą okręgu o środku w punkcie 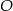 i średnicy długości 15 cm. Odległość punktu
i średnicy długości 15 cm. Odległość punktu 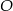 od cięciwy
od cięciwy 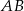 wynosi
wynosi
A) 12 cm B) 7,5 cm C) 6 cm D) 4,5 cm
Cięciwa okręgu o promieniu 15 cm ma długość 24 cm. Odległość środka okręgu od tej cięciwy wynosi
A) 9 cm B) 13 cm C) 8 cm D) 15 cm
Jeśli przyprostokątne trójkąta prostokątnego są równe 6 i 3, a najmniejszy kąt ma miarę  , to wyrażenie
, to wyrażenie 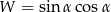 ma wartość
ma wartość
A) 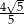 B)
B) 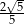 C)
C)  D)
D) 
W trójkącie prostokątnym o przyprostokątnych długości 1 i 2 kąty ostre są równe  i
i 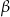 (
(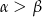 ). Wartość wyrażenia
). Wartość wyrażenia 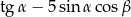 jest równe
jest równe
A) 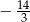 B) -2 C) 0 D)
B) -2 C) 0 D) 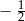
Punkty 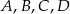 dzielą okrąg o środku
dzielą okrąg o środku 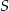 w stosunku
w stosunku 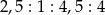 .
.
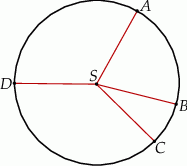
Różnica miar kątów wypukłych 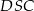 i
i 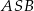 jest równa
jest równa
A) 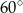 B)
B) 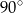 C)
C) 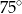 D)
D) 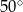
Dany jest trójkąt o bokach długości 4, 5 oraz 6. Cosinus największego kąta wewnętrznego tego trójkąta jest równy
A) 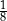 B)
B) 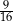 C)
C)  D)
D) 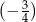
Jeżeli kąt ostry  jest o
jest o 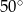 mniejszy od kąta przyległego do niego, to
mniejszy od kąta przyległego do niego, to
A) 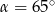 B)
B) 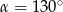 C)
C) 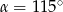 D)
D) 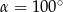
Jeżeli kąt ostry  jest o
jest o 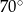 mniejszy od kąta przyległego do niego, to
mniejszy od kąta przyległego do niego, to
A) 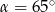 B)
B) 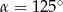 C)
C) 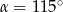 D)
D) 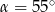
Jeżeli kąt ostry  jest o
jest o 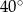 mniejszy od kąta przyległego do niego, to
mniejszy od kąta przyległego do niego, to
A) 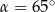 B)
B) 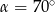 C)
C) 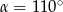 D)
D) 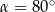
Oblicz długość odcinka 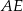 wiedząc, że
wiedząc, że 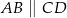 i
i 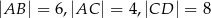 .
.
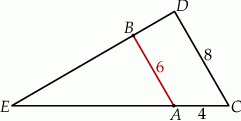
A) 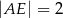 B)
B) 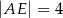 C)
C) 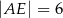 D)
D) 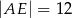
W trójkącie 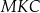 bok
bok 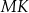 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 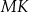 przecina boki
przecina boki 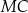 i
i 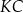 – odpowiednio – w punktach
– odpowiednio – w punktach 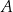 oraz
oraz 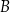 takich, że
takich, że 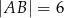 i
i 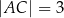 (zobacz rysunek).
(zobacz rysunek).

Długość odcinka 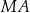 jest równa
jest równa
A) 18 B) 15 C) 9 D) 12
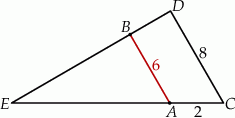
Oblicz długość odcinka 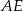 wiedząc, że
wiedząc, że 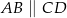 i
i 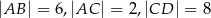 .
.
A) 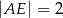 B)
B) 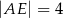 C)
C) 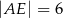 D)
D) 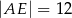
W trójkącie 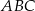 punkt
punkt 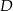 leży na boku
leży na boku 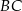 , a punkt
, a punkt 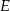 leży na boku
leży na boku 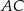 . Odcinek
. Odcinek 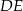 jest równoległy do boku
jest równoległy do boku 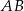 , a ponadto
, a ponadto 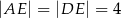 ,
, 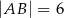 (zobacz rysunek).
(zobacz rysunek).
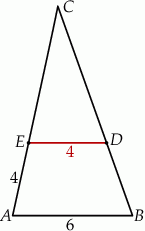
Odcinek 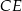 ma długość
ma długość
A) 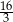 B)
B)  C) 8 D) 6
C) 8 D) 6
W trójkącie 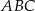 punkt
punkt 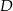 leży na boku
leży na boku 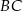 , a punkt
, a punkt 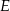 leży na boku
leży na boku 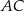 . Odcinek
. Odcinek 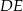 jest równoległy do boku
jest równoległy do boku 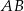 , a ponadto
, a ponadto 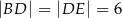 ,
, 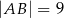 (zobacz rysunek).
(zobacz rysunek).
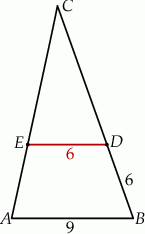
Odcinek 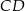 ma długość
ma długość
A) 8 B) 4 C) 9 D) 12
Oblicz długość odcinka 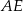 wiedząc, że
wiedząc, że 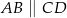 i
i 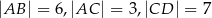 .
.
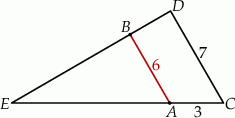
A) 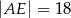 B)
B) 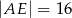 C)
C) 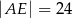 D)
D) 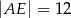
Jeżeli odcinki 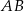 i
i 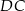 są równoległe, to długość odcinka
są równoległe, to długość odcinka 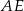 (patrz rys.) jest równa
(patrz rys.) jest równa
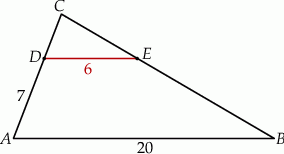
A) 9 B) 10 C) 11 D) 12
Odcinki 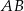 i
i 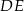 są równoległe. Długości odcinków
są równoległe. Długości odcinków 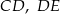 i
i 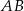 są odpowiednio równe 2, 5 i 15.
są odpowiednio równe 2, 5 i 15.
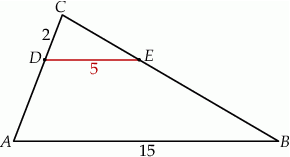
Długość odcinka 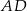 jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Odcinki 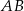 i
i 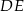 są równoległe. Długości odcinków
są równoległe. Długości odcinków 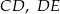 i
i 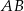 są odpowiednio równe 2, 4 i 16.
są odpowiednio równe 2, 4 i 16.
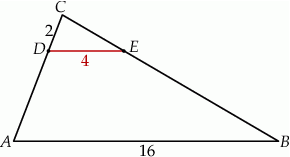
Długość odcinka 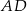 jest równa
jest równa
A) 12 B) 8 C) 3 D) 6
Odcinki 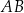 i
i 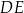 są równoległe. Długości odcinków
są równoległe. Długości odcinków 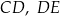 i
i 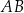 są odpowiednio równe 1, 3 i 9.
są odpowiednio równe 1, 3 i 9.
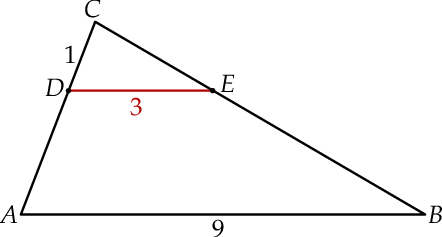
Długość odcinka 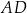 jest równa
jest równa
A) 2 B) 3 C) 5 D) 6
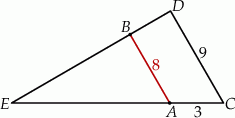
Oblicz długość odcinka 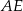 wiedząc, że
wiedząc, że 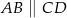 i
i 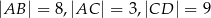 .
.
A) 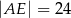 B)
B) 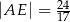 C)
C) 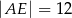 D)
D) 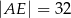
Wysokości 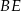 i
i 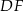 rombu
rombu 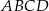 przecinają się w punkcie
przecinają się w punkcie 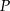 (zobacz rysunek).
(zobacz rysunek).
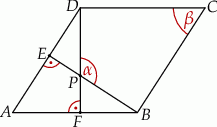
Wyrażenie 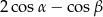 jest równe
jest równe
A) 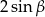 B)
B) 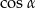 C) 0 D)
C) 0 D) 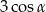
Prostokąt 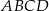 o przekątnej długości
o przekątnej długości 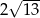 jest podobny do prostokąta o bokach długości 2 i 3. Obwód prostokąta
jest podobny do prostokąta o bokach długości 2 i 3. Obwód prostokąta 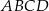 jest równy
jest równy
A) 10 B) 20 C) 5 D) 24
Prostokąt 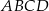 o przekątnej długości
o przekątnej długości 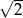 jest podobny do prostokąta o bokach długości 1 i 7. Obwód prostokąta
jest podobny do prostokąta o bokach długości 1 i 7. Obwód prostokąta 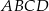 jest równy
jest równy
A) 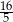 B)
B) 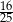 C) 80 D) 16
C) 80 D) 16
Która z liczb nie może być równa polu rombu o obwodzie 12?
A) 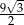 B)
B) 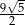 C)
C) 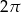 D)
D) 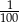
Która z liczb nie może być równa polu rombu o obwodzie 8?
A) 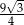 B)
B) 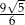 C)
C) 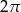 D)
D) 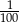
W trójkącie równoramiennym miara kąta przy podstawie jest równa 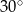 , a ramię ma długość 8 cm. Podstawa tego trójkąta ma długość
, a ramię ma długość 8 cm. Podstawa tego trójkąta ma długość
A) 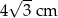 B) 4 cm C)
B) 4 cm C) 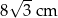 D)
D) 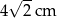
Ramię trójkąta równoramiennego ma długość 12 i tworzy z podstawą kąt o mierze 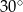 . Obwód tego trójkąta jest równy:
. Obwód tego trójkąta jest równy:
A) 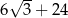 B) 30 C) 36 D)
B) 30 C) 36 D) 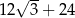
Punkt 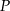 jest punktem wspólnym środkowych
jest punktem wspólnym środkowych 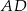 i
i 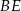 w trójkącie
w trójkącie 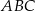 . Wówczas odcinki
. Wówczas odcinki 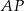 i
i 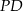 mogą mieć długości
mogą mieć długości
A) 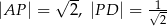 B)
B) 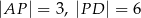
C) 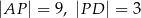 D)
D) 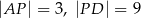
Na okręgu opisanym na kwadracie 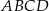 wybrano punkt
wybrano punkt 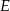 w ten sposób, że
w ten sposób, że 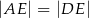 .
.
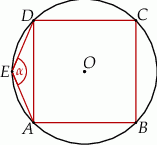
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 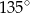 B)
B) 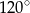 C)
C) 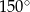 D)
D) 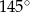
Boki prostokąta mają długości 5 i 12. Sinus kąta pod jakim przecinają się przekątne tego prostokąta jest równy
A) 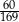 B)
B) 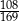 C)
C) 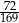 D)
D) 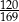
Dany jest okrąg o środku w punkcie 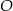 . Prosta
. Prosta 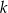 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 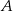 .
.
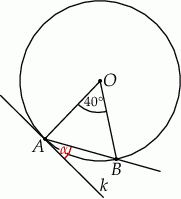
Miara kąta 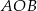 wynosi
wynosi 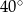 . Wobec tego miara kąta
. Wobec tego miara kąta  jest równa
jest równa
A) 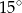 B)
B) 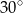 C)
C) 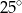 D)
D) 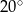
W okręgu o środku 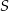 zaznaczono kąt oparty na łuku
zaznaczono kąt oparty na łuku 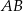 . Przez punkt
. Przez punkt 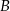 poprowadzono prostą
poprowadzono prostą 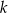 styczną do okręgu.
styczną do okręgu.
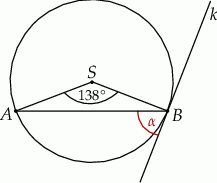
Zaznaczony na rysunku kąt  zawarty między styczną
zawarty między styczną 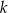 i cięciwą
i cięciwą 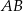 ma miarę
ma miarę
A) 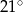 B)
B) 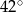 C)
C) 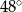 D)
D) 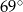
Punkty 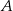 oraz
oraz 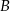 leżą na okręgu o środku
leżą na okręgu o środku 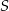 . Kąt środkowy
. Kąt środkowy 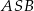 ma miarę
ma miarę 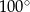 . Prosta
. Prosta 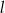 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 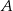 i tworzy z cięciwą
i tworzy z cięciwą 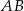 okręgu kąt o mierze
okręgu kąt o mierze  (zobacz rysunek).
(zobacz rysunek).
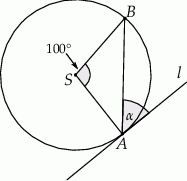
Wtedy
A) 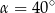 B)
B) 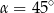 C)
C) 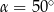 D)
D) 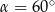
Dany jest okrąg o środku w punkcie 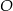 . Prosta
. Prosta 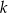 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 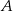 .
.
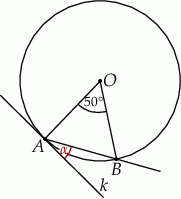
Miara kąta 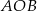 wynosi
wynosi 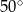 . Wobec tego miara kąta
. Wobec tego miara kąta  jest równa
jest równa
A) 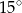 B)
B) 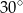 C)
C) 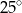 D)
D) 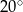
W okręgu o środku 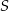 zaznaczono kąt oparty na łuku
zaznaczono kąt oparty na łuku 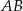 . Przez punkt
. Przez punkt 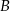 poprowadzono prostą
poprowadzono prostą 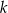 styczną do okręgu.
styczną do okręgu.
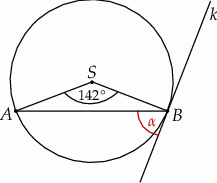
Zaznaczony na rysunku kąt  zawarty między styczną
zawarty między styczną 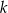 i cięciwą
i cięciwą 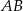 ma miarę
ma miarę
A) 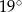 B)
B) 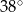 C)
C) 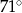 D)
D) 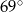
Dany jest okrąg o środku w punkcie 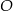 . Prosta
. Prosta 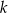 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 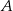 .
.
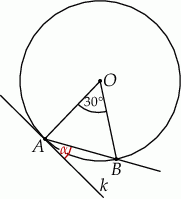
Miara kąta 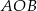 wynosi
wynosi 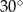 . Wobec tego miara kąta
. Wobec tego miara kąta  jest równa
jest równa
A) 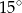 B)
B) 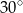 C)
C) 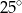 D)
D) 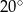
Dany jest trójkąt równoboczny, którego pole jest równe 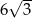 . Bok tego trójkąta ma długość
. Bok tego trójkąta ma długość
A) 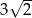 B)
B) 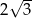 C)
C) 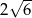 D)
D) 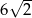
Pole pewnego trójkąta równobocznego jest równe 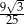 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 4 B) 2 C) 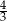 D)
D) 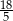
Pole pewnego trójkąta równobocznego jest równe 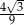 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 4 B) 2 C) 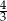 D)
D) 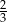
Dany jest trójkąt równoboczny, którego pole jest równe 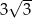 . Bok tego trójkąta ma długość
. Bok tego trójkąta ma długość
A) 3 B) 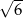 C) 6 D)
C) 6 D) 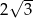
Dane są okrąg o środku 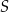 oraz prosta
oraz prosta 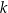 styczna do okręgu w punkcie
styczna do okręgu w punkcie 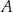 . Odcinek
. Odcinek 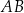 jest cięciwą tego okręgu. Miara kąta ostrego pomiędzy prostą
jest cięciwą tego okręgu. Miara kąta ostrego pomiędzy prostą 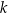 a cięciwą
a cięciwą 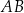 jest równa
jest równa 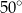 . Punkt
. Punkt 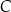 leży na okręgu. Kąt wpisany
leży na okręgu. Kąt wpisany 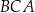 jest ostry.
jest ostry.
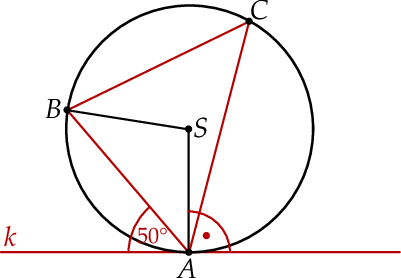
Miara kąta wpisanego 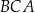 jest równa
jest równa
A) 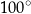 B)
B) 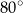 C)
C) 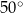 D)
D) 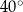
W trójkącie zwiększono długość każdego boku o 20%. O ile procent wzrosło pole tego trójkąta?
A) 20% B) 40% C) 44% D) 400%
