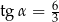Jeżeli  i
i 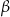 są miarami kątów ostrych trójkąta prostokątnego oraz
są miarami kątów ostrych trójkąta prostokątnego oraz 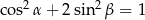 to
to
A) 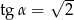 B)
B) 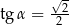 C)
C) 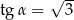 D)
D) 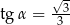
/Szkoła średnia/Zadania testowe/Geometria/Planimetria
Jeżeli  i
i 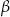 są miarami kątów ostrych trójkąta prostokątnego oraz
są miarami kątów ostrych trójkąta prostokątnego oraz 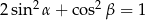 to
to
A) 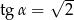 B)
B) 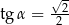 C)
C) 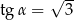 D)
D) 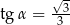
Jeżeli suma miar kąta środkowego i kąta wpisanego opartych na tym samym łuku jest równa 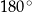 , to kąty te są oparte na
, to kąty te są oparte na
A) 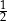 okręgu B)
okręgu B)  okręgu C)
okręgu C)  okręgu D)
okręgu D)  okręgu
okręgu
Czworokąty 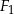 i
i 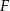 są podobne. Pole czworokąta
są podobne. Pole czworokąta 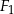 jest o 36% mniejsze od pola czworokąta
jest o 36% mniejsze od pola czworokąta 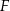 . Obwód czworokąta
. Obwód czworokąta 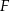 jest większy od obwodu czworokąta
jest większy od obwodu czworokąta 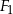 o:
o:
A) 20% B) 25% C) 36% D) 18%
Koło ma promień równy 3. Obwód wycinka tego koła o kącie środkowym 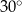 jest równy
jest równy
A) 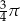 B)
B) 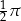 C)
C) 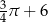 D)
D) 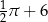
Koło ma promień równy 12. Obwód wycinka tego koła o kącie środkowym 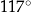 jest równy
jest równy
A) 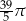 B)
B) 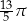 C)
C) 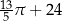 D)
D) 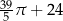
Koło ma promień równy 4. Obwód wycinka tego koła o kącie środkowym 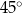 jest równy
jest równy
A) 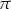 B)
B) 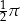 C)
C) 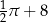 D)
D) 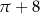
Obwód kwadratu wpisanego w okrąg o długości 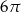 jest równy
jest równy
A) 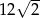 B)
B) 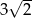 C)
C) 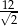 D)
D) 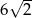
Punkty 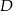 i
i 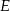 dzielą bok
dzielą bok 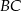 trójkąta
trójkąta 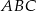 na trzy równe części (zobacz rysunek). Stosunek pól trójkątów
na trzy równe części (zobacz rysunek). Stosunek pól trójkątów 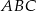 i
i 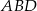 jest równy
jest równy
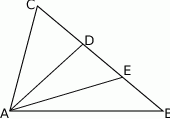
A)  B)
B)  C)
C)  D)
D) 
Pole rombu jest równe 32, a kąt ostry ma miarę 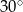 . Wysokość rombu jest równa
. Wysokość rombu jest równa
A) 3 B) 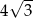 C)
C) 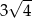 D) 4
D) 4
Pole rombu jest równe 50, a kąt ostry ma miarę 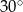 . Wysokość rombu jest równa
. Wysokość rombu jest równa
A) 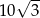 B) 5 C) 10 D)
B) 5 C) 10 D) 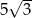
Pole rombu jest równe 18, a kąt ostry ma miarę 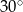 . Wysokość rombu jest równa
. Wysokość rombu jest równa
A) 3 B) 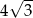 C)
C) 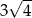 D) 4
D) 4
Dany jest równoramienny trójkąt 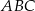 o kącie przy podstawie
o kącie przy podstawie 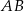 równym
równym 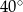 . Punkt
. Punkt 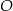 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 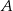 i
i 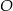 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 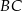 w punkcie
w punkcie 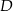 . Jeśli miara kąta
. Jeśli miara kąta 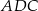 jest równa
jest równa  , to
, to
A) 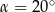 B)
B) 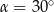 C)
C) 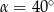 D)
D) 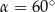
Dany jest równoramienny trójkąt 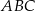 o kącie przy podstawie
o kącie przy podstawie 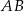 równym
równym 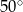 . Punkt
. Punkt 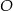 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 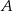 i
i 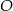 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 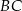 w punkcie
w punkcie 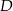 . Jeśli miara kąta
. Jeśli miara kąta 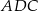 jest równa
jest równa  , to
, to
A) 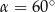 B)
B) 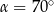 C)
C) 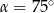 D)
D) 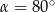
Dany jest równoramienny trójkąt 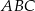 o kącie przy podstawie
o kącie przy podstawie 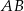 równym
równym 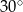 . Punkt
. Punkt 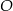 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 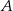 i
i 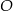 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 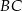 w punkcie
w punkcie 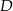 . Jeśli miara kąta
. Jeśli miara kąta 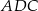 jest równa
jest równa  , to
, to
A) 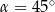 B)
B) 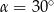 C)
C) 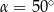 D)
D) 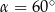
Różnica długości podstaw trapezu równoramiennego o kącie ostrym 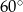 i ramieniu długości 12 może być równa
i ramieniu długości 12 może być równa
A) 6 B) 8 C) 9 D) 12
Odcinek 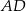 jest dwusieczną w trójkącie równoramiennym
jest dwusieczną w trójkącie równoramiennym 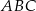 poprowadzoną do ramienia
poprowadzoną do ramienia 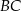 .
.
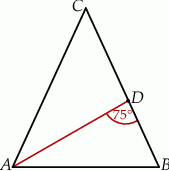
Jeżeli 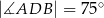 to miara kąta przy wierzchołku
to miara kąta przy wierzchołku 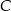 jest równa
jest równa
A) 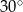 B)
B) 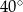 C)
C) 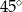 D)
D) 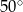
Liczba przekątnych o długości 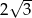 w sześciokącie foremnym o boku długości 2 jest równa
w sześciokącie foremnym o boku długości 2 jest równa
A) 0 B) 3 C) 6 D) 9
W prostokącie 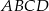 dane są
dane są 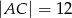 oraz
oraz 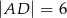 . Wówczas cosinus kąta
. Wówczas cosinus kąta 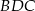 jest równy
jest równy
A) 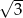 B)
B) 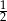 C)
C) 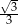 D)
D) 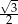
Okrąg jest styczny do boku 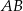 trójkąta
trójkąta 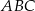 w punkcie
w punkcie 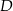 oraz przecina boki
oraz przecina boki 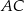 i
i 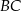 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 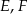 i
i 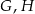 (zobacz rysunek). Kat
(zobacz rysunek). Kat 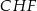 ma miarę
ma miarę 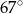 .
.
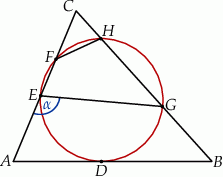
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 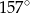 B)
B) 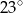 C)
C) 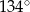 D)
D) 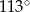
Okrąg jest styczny do boku 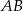 trójkąta
trójkąta 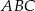 w punkcie
w punkcie 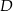 oraz przecina boki
oraz przecina boki 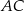 i
i 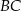 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 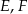 i
i 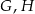 (zobacz rysunek). Kat
(zobacz rysunek). Kat 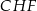 ma miarę
ma miarę 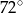 .
.
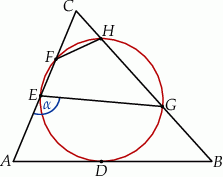
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 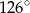 B)
B) 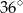 C)
C) 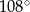 D)
D) 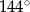
Dane są okręgi styczne wewnętrznie o środkach 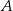 i
i 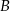 . Wiadomo, że promień jednego okręgu jest trzy razy dłuższy od promienia drugiego okręgu i
. Wiadomo, że promień jednego okręgu jest trzy razy dłuższy od promienia drugiego okręgu i 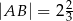 . Promienie tych okręgów mają długość
. Promienie tych okręgów mają długość
A) 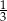 i 3 B)
i 3 B) 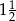 i
i 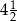 C)
C)  i 2 D)
i 2 D) 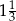 i 4
i 4
Obwód trójkąta prostokątnego równoramiennego wynosi 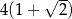 . Długość wysokości poprowadzonej z wierzchołka kąta prostego tego trójkąta jest równa
. Długość wysokości poprowadzonej z wierzchołka kąta prostego tego trójkąta jest równa
A) 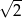 B) 4 C) 2 D)
B) 4 C) 2 D) 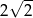
Dany jest trapez równoramienny 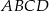 o podstawach
o podstawach 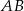 i
i 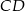 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie 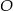 . Jeśli
. Jeśli 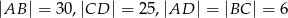 , to
, to
A) 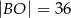 B)
B) 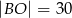 C)
C) 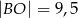 D)
D) 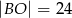
Dany jest trapez równoramienny o podstawach 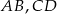 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie 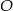 . Jeśli
. Jeśli 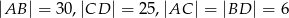 , to
, to
A) 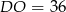 B)
B) 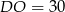 C)
C) 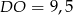 D)
D) 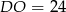
Dany jest trapez równoramienny o podstawach 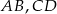 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie 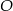 . Jeśli
. Jeśli 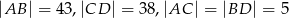 , to
, to
A) 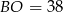 B)
B) 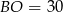 C)
C) 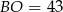 D)
D) 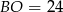
Suma miar kąta wpisanego i kąta środkowego, opartych na 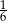 okręgu, jest równa
okręgu, jest równa
A) 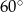 B)
B) 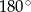 C)
C) 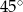 D)
D) 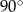
W trójkącie równoramiennym 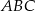 dane są
dane są 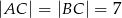 oraz
oraz 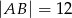 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 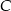 jest równa
jest równa
A) 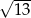 B)
B) 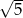 C) 1 D) 5
C) 1 D) 5
W trójkącie równoramiennym 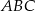 dane są
dane są 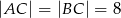 oraz
oraz 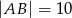 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 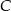 jest równa
jest równa
A) 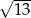 B)
B) 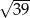 C) 6 D)
C) 6 D) 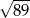
Podstawa trójkąta równoramiennego ma długość 6, a ramię ma długość 5. Wysokość opuszczona na podstawę ma długość
A) 3 B) 4 C) 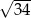 D)
D) 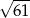
W trójkącie równoramiennym 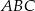 dane są
dane są 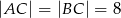 oraz
oraz 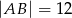 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 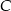 jest równa
jest równa
A) 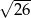 B)
B) 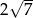 C) 2 D)
C) 2 D) 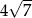
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 13. Wysokość opuszczona na podstawę ma długość
A) 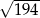 B)
B) 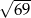 C) 12 D) 11
C) 12 D) 11
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 7. Wysokość opuszczona na podstawę ma długość
A) 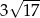 B)
B) 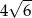 C)
C) 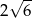 D)
D) 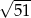
W trójkącie równoramiennym 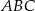 dane są
dane są 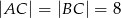 oraz
oraz 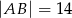 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 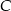 jest równa
jest równa
A) 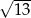 B)
B) 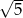 C)
C) 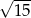 D)
D) 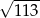
Odcinek 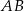 jest średnicą okręgu o środku
jest średnicą okręgu o środku 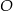 i promieniu
i promieniu  . Na tym okręgu wybrano punkt
. Na tym okręgu wybrano punkt 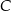 , taki, że
, taki, że 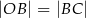 (zobacz rysunek).
(zobacz rysunek).
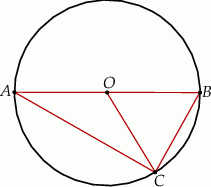
Pole trójkąta 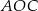 jest równe
jest równe
A) 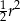 B)
B) 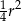 C)
C) 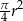 D)
D) 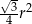
Pole prostokąta przedstawionego na rysunku jest równe 20. Zatem

A) 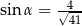 B)
B) 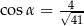 C)
C) 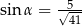 D)
D) 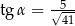
Pole prostokąta przedstawionego na rysunku jest równe 18. Zatem
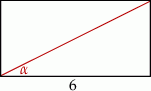
A) 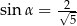 B)
B) 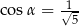 C)
C) 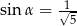 D)
D)