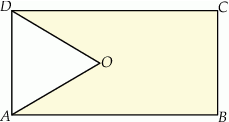
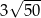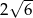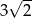Punkty 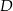 i
i 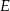 są środkami przyprostokątnych
są środkami przyprostokątnych 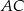 i
i 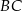 trójkąta prostokątnego
trójkąta prostokątnego 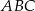 . Punkty
. Punkty 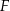 i
i 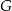 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 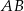 tak, że odcinki
tak, że odcinki 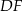 i
i 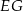 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 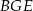 jest równe 1, a pole trójkąta
jest równe 1, a pole trójkąta 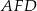 jest równe 4.
jest równe 4.
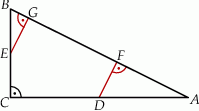
Zatem pole trójkąta  jest równe
jest równe
A) 12 B) 16 C) 18 D) 20

 i
i  trójkąta prostokątnego
trójkąta prostokątnego 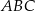 wybrano punkty
wybrano punkty 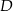 i
i 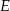 tak, że
tak, że 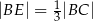 i
i 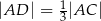 . Punkty
. Punkty 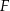 i
i 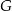 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 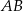 tak, że odcinki
tak, że odcinki 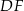 i
i 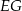 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 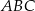 jest równe 36.
jest równe 36. 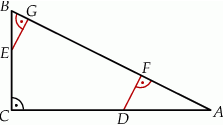
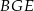 i
i 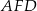 jest równa
jest równa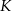 i
i 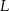 są środkami przyprostokątnych
są środkami przyprostokątnych 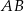 i
i 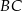 trójkąta prostokątnego
trójkąta prostokątnego 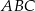 . Punkty
. Punkty 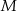 i
i 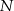 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 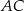 tak, że odcinki
tak, że odcinki 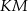 i
i 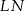 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 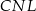 jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta 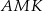 jest równe 5.
jest równe 5. 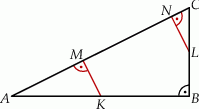
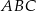 jest równe
jest równe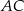 i
i 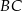 trójkąta prostokątnego
trójkąta prostokątnego 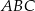 wybrano punkty
wybrano punkty 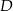 i
i 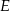 tak, że
tak, że 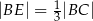 i
i 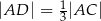 . Punkty
. Punkty 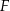 i
i 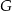 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 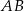 tak, że odcinki
tak, że odcinki 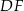 i
i 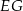 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 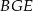 jest równe 1, a pole trójkąta
jest równe 1, a pole trójkąta 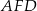 jest równe 4.
jest równe 4. 
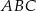 jest równe
jest równe , takim, że
, takim, że 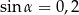 . Długość przekątnej tego prostokąta jest równa
. Długość przekątnej tego prostokąta jest równa 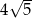
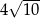
 (
(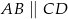 ) wysokość
) wysokość 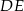 podzieliła podstawę na odcinki długości
podzieliła podstawę na odcinki długości 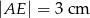 i
i 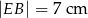 . Odcinek łączący środki ramion w tym trapezie ma długość
. Odcinek łączący środki ramion w tym trapezie ma długość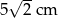
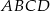 (
(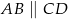 ) wysokość
) wysokość 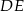 podzieliła podstawę na odcinki długości
podzieliła podstawę na odcinki długości 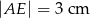 i
i 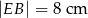 . Odcinek łączący środki ramion w tym trapezie ma długość
. Odcinek łączący środki ramion w tym trapezie ma długość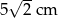
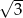 . Najmniejszy kąt w tym trójkącie ma miarę
. Najmniejszy kąt w tym trójkącie ma miarę 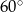
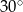
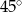
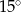
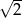 i
i 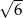 . Największy kąt ostry w tym trójkącie ma miarę
. Największy kąt ostry w tym trójkącie ma miarę 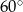
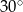
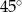
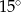
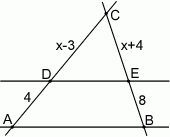
 odcinek
odcinek 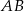 jest równoległy do odcinka
jest równoległy do odcinka 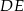 ?
? 
 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku  . Jeśli
. Jeśli  i
i 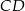 jest średnicą okręgu, to miara kąta
jest średnicą okręgu, to miara kąta 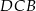 jest równa
jest równa 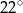
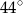
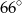
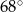
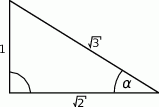
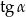 jest równy
jest równy 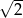
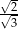
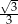
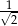
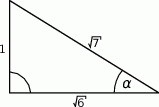
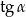 jest równy
jest równy 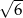
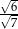
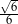
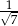
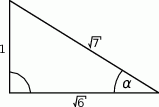
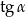 jest równy
jest równy 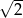
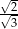
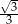
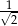
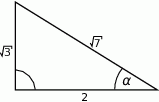
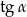 jest równy
jest równy 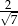
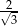
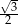
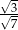
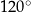
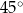
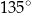
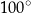
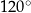
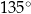
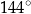
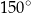
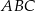 i
i 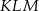 o polach równych – odpowiednio –
o polach równych – odpowiednio – 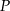 oraz
oraz 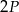 . Obwód trójkąta
. Obwód trójkąta 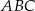 jest równy
jest równy  . Obwód trójkąta
. Obwód trójkąta 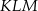 jest równy
jest równy 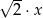 ,
,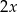 ,
,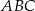 i
i 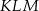 o polach równych – odpowiednio –
o polach równych – odpowiednio – 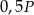 oraz
oraz 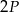 . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 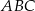 jest równy
jest równy  . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 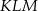 jest równy
jest równy 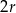 ,
,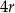 ,
,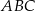 (patrz rysunek) ma miarę
(patrz rysunek) ma miarę 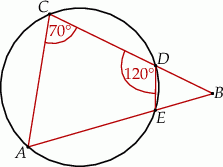
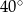
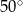
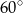
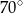
 jest równa
jest równa 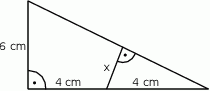
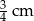
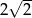 . Pole tego sześciokąta jest równe
. Pole tego sześciokąta jest równe 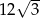
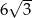
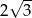
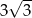
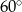 i ramieniu długości
i ramieniu długości 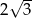 jest równa
jest równa 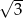
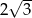
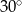 i ramieniu długości
i ramieniu długości 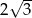 jest równa
jest równa 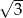
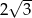
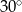 i ramieniu długości
i ramieniu długości 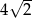 jest równa
jest równa 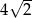
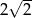
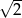
 i
i 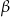 są kątami przyległymi. Kąt wyznaczony przez dwusieczne kątów
są kątami przyległymi. Kąt wyznaczony przez dwusieczne kątów  oraz
oraz 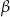 ma miarę
ma miarę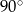
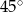
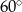
 i
i 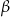
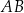 i
i 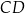 okręgu są oparte kąty wpisane
okręgu są oparte kąty wpisane 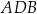 i
i 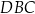 , takie, że
, takie, że 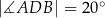 i
i 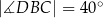 (zobacz rysunek). Cięciwy
(zobacz rysunek). Cięciwy 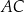 i
i 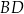 przecinają się w punkcie
przecinają się w punkcie 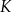 .
. 
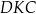 jest równa
jest równa 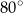
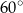
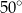
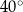
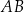 i
i 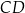 okręgu są oparte kąty wpisane
okręgu są oparte kąty wpisane 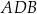 i
i 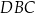 , takie, że
, takie, że 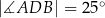 i
i 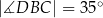 (zobacz rysunek). Cięciwy
(zobacz rysunek). Cięciwy 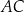 i
i 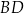 przecinają się w punkcie
przecinają się w punkcie 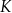 .
. 
 jest równa
jest równa 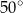
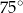
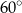
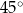
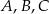 czworokąta
czworokąta 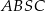 leżą na okręgu o środku
leżą na okręgu o środku 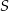 . Kąt
. Kąt 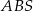 ma miarę
ma miarę 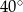 (zobacz rysunek), a przekątna
(zobacz rysunek), a przekątna  jest dwusieczną tego kąta.
jest dwusieczną tego kąta. 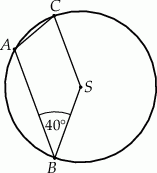
 jest równa
jest równa 
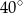
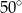
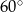
 przecinają się w punkcie
przecinają się w punkcie 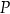 odległym od wierzchołka
odległym od wierzchołka 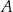 o 6 cm. Wobec tego środkowa poprowadzona na bok
o 6 cm. Wobec tego środkowa poprowadzona na bok 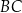 ma długość
ma długość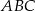 przecinają się w punkcie
przecinają się w punkcie 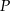 odległym od wierzchołka
odległym od wierzchołka 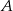 o 6 cm. Środkowa opuszczona na bok
o 6 cm. Środkowa opuszczona na bok 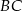 przecina ten bok w punkcie
przecina ten bok w punkcie 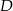 . Wobec tego długość odcinka
. Wobec tego długość odcinka 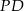 wynosi
wynosi przecinają się w punkcie
przecinają się w punkcie 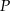 , przy czym długość środkowej opuszczonej na bok
, przy czym długość środkowej opuszczonej na bok  ma długość 9 cm. Wobec tego długość odcinka
ma długość 9 cm. Wobec tego długość odcinka 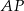 wynosi
wynosi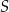 jest środkiem ciężkości trójkąta
jest środkiem ciężkości trójkąta 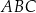 . Długość odcinka
. Długość odcinka 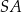 jest równa 10. Długość środkowej poprowadzonej z wierzchołka
jest równa 10. Długość środkowej poprowadzonej z wierzchołka 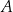 do boku
do boku 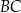 jest równa
jest równa 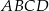 o obwodzie 30 wycięto trójkąt równoboczny
o obwodzie 30 wycięto trójkąt równoboczny 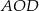 o obwodzie 15 (tak jak na rysunku).
o obwodzie 15 (tak jak na rysunku).