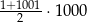Cenę  (w złotych) pewnego towaru obniżono najpierw o 30%, a następnie obniżono o 20% w odniesieniu do ceny obowiązującej w danym momencie. Po obydwu tych obniżkach cena towaru jest równa
(w złotych) pewnego towaru obniżono najpierw o 30%, a następnie obniżono o 20% w odniesieniu do ceny obowiązującej w danym momencie. Po obydwu tych obniżkach cena towaru jest równa
A) 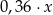 złotych. B)
złotych. B) 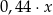 złotych.
złotych.
C) 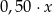 złotych. D)
złotych. D) 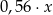 złotych.
złotych.
/Szkoła średnia/Zadania testowe/Zadania z treścią
Grupa uczniów jechała pociągiem w góry. Jedna siódma uczniów miała miejsca przy oknie, jedna piąta uczniów miała miejsca przy korytarzu, a pozostali uczniowie mieli miejsca środkowe.
Jaki procent wszystkich uczniów stanowią uczniowie, którzy nie mieli miejsc przy korytarzu?
A) 75% B) 60% C) 20% D) 80%
Słoń waży 5 ton, a waga mrówki jest równa 0,5 grama. Ile razy słoń jest cięższy od mrówki?
A) 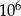 B)
B) 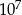 C) 10 D)
C) 10 D) 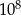
Wieża Eiffla ma wysokość 300 m, a pantofelek ma długość 0,3 mm. Ile razy wieża Eiffla jest wyższa od długości pantofelka?
A) 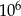 B)
B) 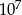 C) 1000 D)
C) 1000 D) 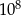
W pewnym zoo mieszkają słoń afrykański o masie 6 ton oraz góralek skalny o masie 3 kg. Masa słonia afrykańskiego jest większa niż masa góralka skalnego
A) 20 razy. B) 200 razy. C) 2 000 razy. D) 20 000 razy.
Cenę telewizora obniżono o 15%, a następnie o 2%. Klient kupił telewizor po obniżonej cenie i dzięki temu zapłacił o 501 zł mniej, niż zapłaciłby przed obniżkami. Przed obniżkami ten telewizor kosztował
A) 2947 zł B) 4000 zł C) 3000 zł D) 2840 zł
Cenę laptopa podwyższono o 12%, a następnie o 19%. W wyniku tych podwyżek cena laptopa wzrosła o 832 zł. Przed podwyżkami ten laptop kosztował
A) 3332 zł B) 2500 zł C) 3000 zł D) 2375 zł
Firma przeprowadziła badania rynkowe dotyczące wpływu zmiany ceny 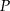 swojego produktu na liczbę
swojego produktu na liczbę 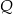 kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 6 jednostek powoduje spadek liczby kupujących o 9 jednostek. Ponadto przy cenie równej 9 jednostek liczba kupujących jest równa 24 jednostki. Liczba kupujących ten produkt przy cenie równej 19 jednostek jest równa
kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 6 jednostek powoduje spadek liczby kupujących o 9 jednostek. Ponadto przy cenie równej 9 jednostek liczba kupujących jest równa 24 jednostki. Liczba kupujących ten produkt przy cenie równej 19 jednostek jest równa
A) 10 jednostek B) 13 jednostek
C) 11 jednostek D) 9 jednostek
W pewnej szkole liczącej 500 uczniów 80% uczy się języka angielskiego, 49% – języka rosyjskiego, a 37% uczy się obu tych języków. Wynika stąd, że liczba uczniów, którzy nie uczą się żadnego z tych języków, to
A) 50 B) 40 C) 37 D) 167
W pewnej szkole liczącej 400 uczniów 83% uczy się języka angielskiego, 51% – języka rosyjskiego, a 42% uczy się obu tych języków. Wynika stąd, że liczba uczniów, którzy nie uczą się żadnego z tych języków, to
A) 56 B) 48 C) 168 D) 32
W pewnej szkole liczącej 600 uczniów 76% uczniów uczy się języka angielskiego, 38% – języka niemieckiego, a 26% uczy się obu tych języków. Wynika stąd, że liczba uczniów, którzy nie uczą się żadnego z tych języków, to
A) 72 B) 60 C) 108 D) 96
Cenę pewnego towaru obniżono o 25%. O ile procent należy podnieść obecną cenę tego towaru, aby otrzymać cenę początkową?
A) o 20% B) o 33,(3)% C) o 15,(2)% D) o 22%
Cenę pewnego towaru obniżono o 20%. O ile procent należy podnieść obecną cenę tego towaru, aby otrzymać cenę początkową?
A) o 20% B) o 33,(3)% C) o 25% D) o 30%
Cenę  pewnego towaru obniżono o 36% i otrzymano cenę
pewnego towaru obniżono o 36% i otrzymano cenę 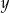 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 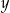 należy podnieść o
należy podnieść o
A) o 64% B) o 60% C) o 36% D) o 56,25%
Cenę  pewnego towaru obniżono o 20% i otrzymano cenę
pewnego towaru obniżono o 20% i otrzymano cenę 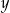 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 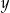 należy podnieść o
należy podnieść o
A) o 25% B) o 20% C) o 15% D) o 12%
Cenę nart obniżono latem o 20%, a potem jeszcze o 15%. Po tych dwóch obniżkach narty kosztowały 705 zł i 50 gr. Wynika z tego, że pierwotna cena nart to
A) 952,42 zł B) 980 zł C) 1037,5 zł D) 1100 zł
Cenę aparatu fotograficznego obniżono o 15%, a następnie – o 20% w odniesieniu do ceny obowiązującej w danym momencie. Po tych dwóch obniżkach aparat kosztuje 340 zł. Przed obiema obniżkami cena tego aparatu była równa
A) 500 zł B) 425 zł C) 400 zł D) 375 zł
Cenę płetw obniżono zimą o 14%, a potem jeszcze o 20%. Po tych dwóch obniżkach płetwy kosztowały 242 zł i 52 gr. Wynika z tego, że pierwotna cena płetw to
A) 331,77 zł B) 352,5 zł C) 347 zł D) 395 zł
Cenę pontonu obniżono zimą o 15%, a potem jeszcze o 25%. Po tych dwóch obniżkach ponton kosztował 1912 zł i 50 gr. Wynika z tego, że pierwotna cena pontonu to
A) 3000 zł B) 2749,22 zł C) 2974,22 zł D) 2000 zł
W pewnym zakładzie pracy w wyniku dwóch podwyżek zwiększono pensje pracowników o 26%. W ramach pierwszej z tych podwyżek płace zwiększono o 20%. O ile procent zwiększono płace w ramach drugiej podwyżki?
A) o 12% B) o 6% C) o 5% D) o 10%
W wyniku dwóch obniżek cenę komputera obniżono o 40%. Druga z tych obniżek była obniżką o 25%. O ile procent obniżono cenę komputera przy pierwszej obniżce?
A) o 15% B) o 65% C) o 20% D) o 30%
W wyniku dwóch obniżek cenę spodni obniżono o 52%. W ramach pierwszej z tych obniżek cenę zmniejszono o 20%. O ile procent zmniejszono cenę w ramach drugiej obniżki?
A) o 60% B) o 40% C) o 20% D) o 50%
Na seans filmowy sprzedano 280 biletów, w tym 126 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 22% B) 33% C) 45% D) 63%
Na seans filmowy sprzedano 280 biletów, w tym 84 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 14% B) 22% C) 30% D) 42%
Na seans filmowy sprzedano 420 biletów, w tym 189 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 63% B) 45% C) 33% D) 22%
Na koncert sprzedano 680 biletów, w tym 306 na miejsca siedzące. Jaki procent sprzedanych biletów stanowiły bilety na miejsca siedzące?
A) 63% B) 45% C) 33% D) 22%
Wykonując rozmowę telefoniczną płacimy 63 grosze za rozpoczęcie połączenia oraz 42 grosze za każdą minutę połączenia. Ile minut trwała rozmowa, której łączny koszt wyniósł 16,17 zł?
A) 38 B) 36 C) 43 D) 37
Wykonując rozmowę telefoniczną płacimy 43 grosze za rozpoczęcie połączenia oraz 32 grosze za każdą minutę połączenia. Ile minut trwała rozmowa, której łączny koszt wyniósł 12,59 zł?
A) 39 B) 37 C) 38 D) 44
Spodnie po obniżce ceny o 30% kosztują 126 zł. Ile kosztowały spodnie przed obniżką?
A) 163,80 zł B) 180 zł C) 294 zł D) 420 zł
Medyczna maseczka ochronna wielokrotnego użytku z wymiennymi filtrami wskutek podwyżki zdrożała o 40% i kosztuje obecnie 106,40 zł. Cena maseczki przed podwyżką była równa
A) 63,84 zł B) 65,40 zł C) 76,00 zł D) 66,40 zł
Koszt uczestnictwa w obozie sportowym w 2018 r. wynosi 1620 zł. Wzrósł on w stosunku do kosztu z 2017 r. o 35%. Koszt uczestnictwa w obozie w 2017 r. wynosił
A) 1215 zł B) 1053 zł C) 1200 zł D) 567 zł
Spodnie po obniżce ceny o 25% kosztują 168 zł. Ile kosztowały spodnie przed obniżką?
A) 193 zł B) 210 zł C) 224 zł D) 336 zł
Cena książki wzrosła o 15% i wynosi 92 zł. Ile kosztowała książka przed podwyżką?
A) 105,8 zł B) 77 zł C) 78,2 zł D) 80 zł
Cena roweru po obniżce o 15% była równa 850 zł. Przed obniżką ten rower kosztował
A) 865,00 zł B) 850,15 zł C) 1000,00 zł D) 977,50 zł
Cenę pewnego towaru obniżono najpierw o 30%, a potem o 50%. Początkowa cena została więc ostatecznie obniżona o 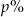 . Wynika stąd, że
. Wynika stąd, że
A) 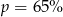 B)
B) 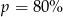 C)
C) 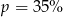 D)
D) 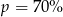
Cenę książki obniżano dwukrotnie, najpierw o 10%, a po miesiącu jeszcze o 5%. W wyniku obu obniżek cena książki zmniejszyła się o
A) 14% B) 14,5% C) 15% D) 15,5%
Cenę nart obniżono o 20%, a po miesiącu nową cenę obniżono o dalsze 30%. W wyniku obniżek cena nart zmniejszyła się o
A) 44% B) 50% C) 56% D) 60%
Cenę biurka obniżono o 10%, a następnie nową cenę obniżono o 30%. W wyniku obu tych zmian cena biurka zmniejszyła się w stosunku do ceny sprzed obu obniżek o
A) 43% B) 40% C) 37% D) 63%
Cenę pewnego towaru obniżono najpierw o 20%, a potem o 30%. Początkowa cena została więc ostatecznie obniżona o 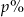 . Wynika stąd, że
. Wynika stąd, że
A) 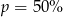 B)
B) 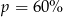 C)
C) 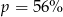 D)
D) 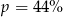
Cena towaru została podwyższona o 30%, a po pewnym czasie nową, wyższą cenę ponownie podwyższono, tym razem o 10%. W rezultacie obu podwyżek wyjściowa cena towaru zwiększyła się o
A) 15% B) 20% C) 40% D) 43%
Cenę pewnego towaru podwyższono najpierw o 20%, a potem jeszcze o 10%. Rzeczywista podwyżka w procentach wyniosła
A) 20% B) 30% C) 32% D) 34%
Cenę komputera obniżano dwukrotnie, najpierw o 20%, a po miesiącu jeszcze o 10%. W wyniku obu obniżek cena komputera zmniejszyła się o
A) 31% B) 30% C) 29% D) 28%
Cenę pewnego towaru obniżano dwukrotnie, za każdym razem o 20%. Takie dwie obniżki ceny tego towaru można zastąpić równoważną im jedną obniżką
A) o 40% B) o 36% C) o 32% D) o 28%
Cenę pewnego towaru obniżono o 20%, a następnie nową cenę tego towaru obniżono o 30%. Takie dwie obniżki ceny tego towaru można zastąpić równoważną im jedną obniżką
A) o 50% B) o 56% C) o 44% D) o 66%
Cenę pewnego towaru podwyższono o 20%, a następnie nową cenę tego towaru podwyższono o 30%. Takie dwie podwyżki ceny tego towaru można zastąpić równoważną im jedną podwyżką
A) o 50% B) o 56% C) o 60% D) o 66%
Cenę książki obniżono o 20%, a po miesiącu nową cenę obniżono o dalsze 10%. W wyniku obu obniżek cena książki zmniejszyła się o
A) 25% B) 28% C) 29% D) 30%
Cenę pewnego towaru podwyższono najpierw o 10%, a potem jeszcze o 10%. Rzeczywista podwyżka w procentach wyniosła
A) 20% B) 21% C) 22% D) 10%
Cenę pewnego towaru obniżono najpierw o 40%, a potem o 70%. Początkowa cena została więc ostatecznie obniżona o 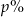 . Wynika stąd, że
. Wynika stąd, że
A) 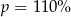 B)
B) 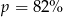 C)
C) 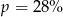 D)
D) 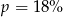
Cenę towaru obniżano dwa razy. Pierwsza obniżka wynosiła 10%, a druga 20%. O ile procent w wyniku obu obniżek spadła cena towaru?
A) o 24% B) o 26% C) o 28% D) o 30%
Cenę drukarki obniżono o 20%, a następnie nową cenę obniżono o 10%. W wyniku obu tych zmian cena drukarki zmniejszyła się w stosunku do ceny sprzed obu obniżek o
A) 18% B) 28% C) 30% D) 72%
Czas 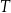 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 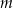 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
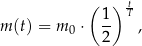
gdzie:
-
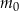 – masa przyjętej dawki leku,
– masa przyjętej dawki leku, -
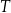 – czas półtrwania leku,
– czas półtrwania leku, -
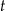 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.
W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie.
Pacjent otrzymuje co 4 dni o tej samej godzinie dawkę 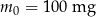 leku L. Czas półtrwania tego leku w organizmie jest równy
leku L. Czas półtrwania tego leku w organizmie jest równy 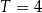 doby.
doby.
Wykres zależności masy 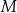 leku L w organizmie tego pacjenta od czasu
leku L w organizmie tego pacjenta od czasu 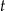 , liczonego od momentu przyjęcia przez pacjenta pierwszej dawki, przedstawiono na rysunku
, liczonego od momentu przyjęcia przez pacjenta pierwszej dawki, przedstawiono na rysunku
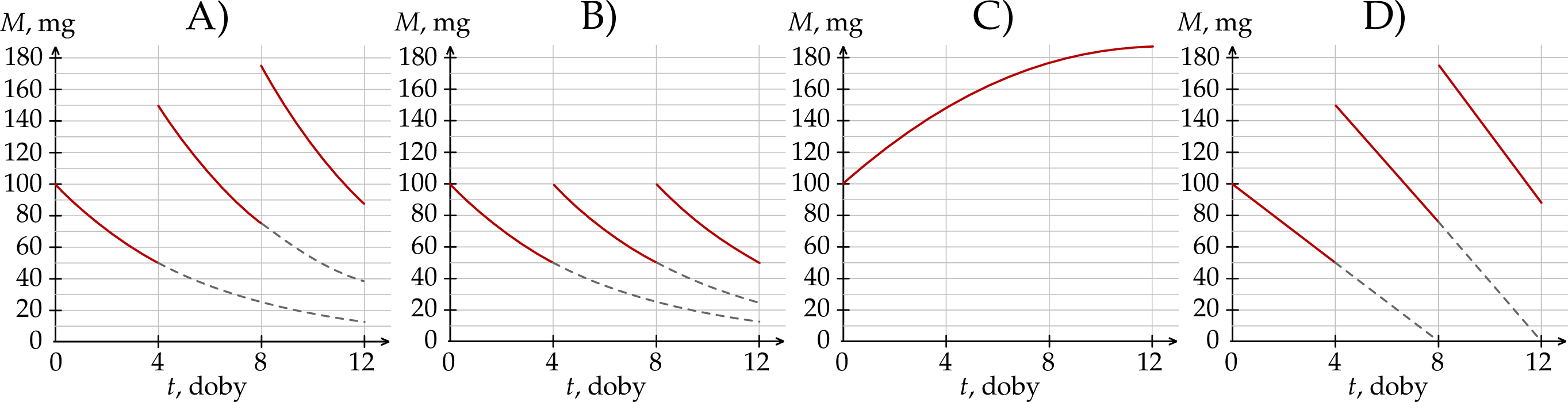
Czas 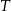 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 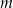 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
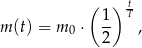
gdzie: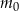 – masa przyjętej dawki leku
– masa przyjętej dawki leku 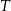 – czas półtrwania leku
– czas półtrwania leku 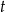 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.
W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie.
Pan Karol otrzymuje codziennie o godz. 12:00 dawkę 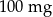 leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę
leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę 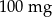 tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy
tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy 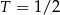 doby.
doby.
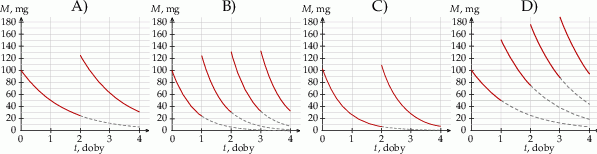
Wykres zależności masy 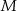 leku L w organizmie pana Karola od czasu
leku L w organizmie pana Karola od czasu 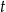 , liczonego od momentu przyjęcia przez niego pierwszej dawki, przedstawiono na rysunku
, liczonego od momentu przyjęcia przez niego pierwszej dawki, przedstawiono na rysunku
Koszt brutto wysłania SMS-a w usłudze Premium SMS wynosi 17,22 zł. Jaka jest wartość netto tego SMS-a, jeżeli koszt SMS-a obciążony jest 19% podatkiem dochodowym oraz 23% podatkiem VAT?
A) 7,12 zł B) 10,74 zł C) 25,20 zł D) 11,76 zł
Stężenie roztworu początkowo wzrosło o 30%, a po 10 minutach wzrosło o dalsze 20%. W wyniku tych zmian stężenie wzrosło o
A) 44% B) 50% C) 56% D) 60%
Stężenie roztworu początkowo wzrosło o 20%, a po 15 minutach wzrosło o dalsze 30%. W wyniku tych zmian stężenie wzrosło o
A) 44% B) 56% C) 50% D) 60%
Stężenie roztworu początkowo wzrosło o 25%, a po 10 minutach wzrosło o dalsze 20%. W wyniku tych zmian stężenie wzrosło o
A) 45% B) 50% C) 55% D) 60%
Kostka mydła ma kształt prostopadłościanu. Załóżmy, że po tygodniu używania każdy z wymiarów kostki zmniejszył się o połowę. Pozostała ilość mydła (przy takim samym użytkowaniu) wystarczy na
A) 1 dzień B) 2 dni C) 5 dni D) 7 dni
Cena długopisu po 3 podwyżkach o 50% i dwóch obniżkach o 20% wzrosła o 2,32 zł. Nowa cena długopisu jest równa
A) 3,42 zł B) 2 zł C) 4,32 zł D) 2,34 zł
Cena długopisu po 2 podwyżkach o 20% i trzech obniżkach o 50% zmalała o 2,87 zł. Nowa cena długopisu jest równa
A) 1,26 zł B) 0,63 zł C) 3,50 zł D) 6,37 zł
Cena telewizora po 3 podwyżkach o 25% i dwóch obniżkach o 20% wzrosła o 1200 zł. Nowa cena telewizora jest równa
A) 4800 zł B) 5760 zł C) 6000 zł D) 4500 zł
Jeśli liczbę  powiększymy o 3, to otrzymamy
powiększymy o 3, to otrzymamy  tej liczby. Wynika stąd, że
tej liczby. Wynika stąd, że
A) 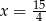 B)
B) 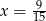 C)
C) 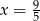 D)
D) 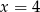
Jeśli liczbę  powiększymy o 4, to otrzymamy
powiększymy o 4, to otrzymamy 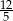 tej liczby. Wynika stąd, że
tej liczby. Wynika stąd, że
A) 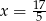 B)
B) 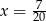 C)
C) 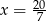 D)
D) 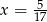
Jeśli liczbę  powiększymy o 5, to otrzymamy
powiększymy o 5, to otrzymamy  tej liczby. Wynika stąd, że
tej liczby. Wynika stąd, że
A) 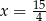 B)
B) 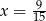 C)
C) 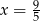 D)
D) 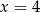
Suma kolejnych dodatnich liczb nieparzystych mniejszych od 100 jest równa
A) 2500 B) 5050 C) 2450 D) 2525
Suma wszystkich liczb całkowitych dodatnich parzystych i jednocześnie mniejszych od 1001 jest równa
A) 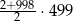 B)
B) 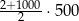 C)
C) 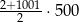 D)
D) 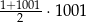
Suma kolejnych liczb dodatnich parzystych mniejszych od 100 jest równa
A) 2550 B) 4900 C) 2450 D) 2525
Suma kolejnych dodatnich liczb nieparzystych mniejszych od 200 jest równa
A) 9801 B) 10201 C) 9900 D) 10000
Suma wszystkich liczb całkowitych dodatnich nieparzystych i jednocześnie mniejszych od 1000 jest równa
A) 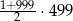 B)
B) 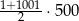 C)
C) 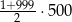 D)
D)