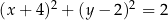Okręgi o środkach 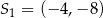 oraz
oraz 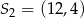 są styczne wewnętrznie. Promień pierwszego z tych okręgów jest 6 razy większy od promienia drugiego okręgu. Suma promieni tych okręgów jest równa
są styczne wewnętrznie. Promień pierwszego z tych okręgów jest 6 razy większy od promienia drugiego okręgu. Suma promieni tych okręgów jest równa
A) 28 B) 24 C) 20 D) 16
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Okrąg
Okrąg o środku 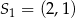 i promieniu
i promieniu  oraz okrąg o środku
oraz okrąg o środku 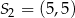 i promieniu 6 są styczne wewnętrznie. Wtedy
i promieniu 6 są styczne wewnętrznie. Wtedy
A) 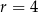 B)
B) 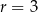 C)
C) 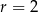 D)
D) 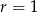
Liczba punktów wspólnych okręgu 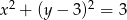 i prostej
i prostej 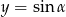 , gdzie
, gdzie  jest kątem ostrym jest równa
jest kątem ostrym jest równa
A) 0 B) 1 C) 2 D) 3
Liczba punktów wspólnych okręgu 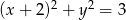 i prostej
i prostej 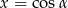 , gdzie
, gdzie  jest kątem ostrym jest równa
jest kątem ostrym jest równa
A) 3 B) 2 C) 1 D) 0
Liczba punktów wspólnych okręgu 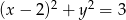 i prostej
i prostej 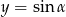 , gdzie
, gdzie  jest kątem ostrym jest równa
jest kątem ostrym jest równa
A) 0 B) 1 C) 2 D) 3
Środkiem okręgu jest punkt 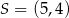 . Do okręgu należy punkt
. Do okręgu należy punkt 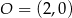 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 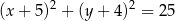 B)
B) 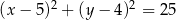
C) 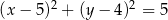 D)
D) 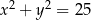
Punkt 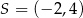 jest środkiem okręgu. Na okręgu leży punkt
jest środkiem okręgu. Na okręgu leży punkt 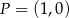 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 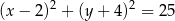 B)
B) 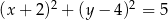
C) 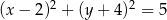 D)
D) 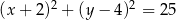
Środkiem okręgu jest punkt 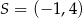 . Do okręgu należy punkt
. Do okręgu należy punkt 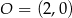 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 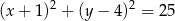 B)
B) 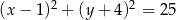
C) 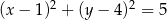 D)
D) 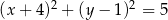
Środkiem okręgu jest punkt 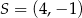 . Do okręgu należy punkt
. Do okręgu należy punkt 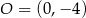 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 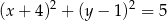 B)
B) 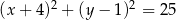
C) 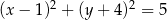 D)
D) 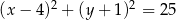
Okrąg przedstawiony na rysunku ma środek w punkcie 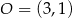 i przechodzi przez punkty
i przechodzi przez punkty 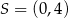 i
i 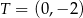 . Okrąg ten jest opisany przez równanie
. Okrąg ten jest opisany przez równanie
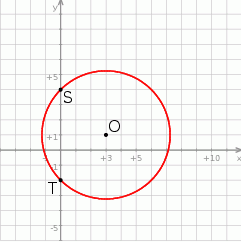
A) 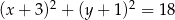 B)
B) 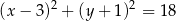
C) 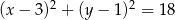 D)
D) 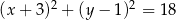
Okrąg, którego środkiem jest punkt 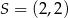 , jest styczny do prostej
, jest styczny do prostej 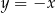 . Promień tego okręgu jest równy
. Promień tego okręgu jest równy
A) 2 B) 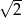 C)
C) 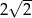 D) 4
D) 4
Wskaż wartość parametru 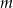 , dla którego prosta
, dla którego prosta 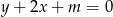 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 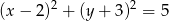
A) 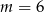 B)
B) 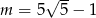 C)
C) 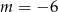 D)
D) 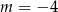
Wskaż wartość parametru 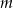 , dla którego prosta
, dla którego prosta 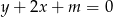 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 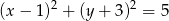
A) 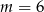 B)
B) 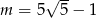 C)
C) 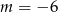 D)
D) 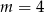
Okręgi 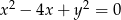 i
i 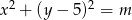 , gdzie
, gdzie 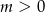 są styczne zewnętrznie. Zatem
są styczne zewnętrznie. Zatem
A) 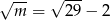 B)
B) 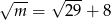 C)
C) 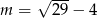 D)
D) 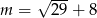
20% pola ograniczonego okręgiem o równaniu 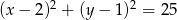 wynosi
wynosi
A) 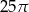 B)
B) 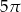 C)
C) 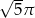 D)
D) 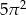
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 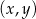 , dany jest okrąg
, dany jest okrąg 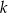 o środku
o środku 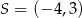 . Jednym z punktów leżących na tym okręgu jest
. Jednym z punktów leżących na tym okręgu jest 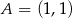 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Punkt 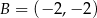 należy do okręgu należy do okręgu 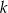 . . | P | F |
Promień okręgu 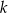 jest równy 29. jest równy 29. | P | F |
Okrąg o środku 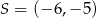 jest styczny do osi
jest styczny do osi 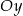 układu współrzędnych w punkcie
układu współrzędnych w punkcie 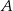 oraz jest styczny do prostej
oraz jest styczny do prostej 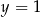 w punkcie
w punkcie 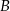 . Promień okręgu o średnicy
. Promień okręgu o średnicy 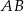 jest równy
jest równy
A) 6 B) 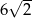 C) 12 D)
C) 12 D) 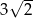
Punkty 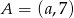 i
i 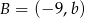 są końcami średnicy okręgu o środku
są końcami średnicy okręgu o środku 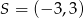 . Wtedy
. Wtedy
A) 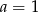 B)
B) 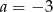 C)
C) 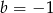 D)
D) 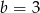
Punkty 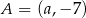 i
i 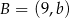 są końcami średnicy okręgu o środku
są końcami średnicy okręgu o środku 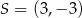 . Wtedy
. Wtedy
A) 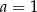 B)
B) 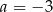 C)
C) 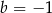 D)
D) 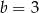
Punkty 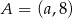 i
i 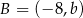 są końcami średnicy okręgu o środku
są końcami średnicy okręgu o środku 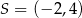 . Wtedy
. Wtedy
A) 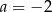 B)
B) 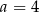 C)
C) 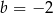 D)
D) 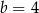
W kartezjańskim układzie współrzędnych 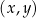 dane są: punkt
dane są: punkt 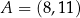 oraz okrąg o równaniu
oraz okrąg o równaniu 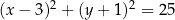 . Odległość punktu
. Odległość punktu 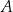 od środka tego okręgu jest równa
od środka tego okręgu jest równa
A) 25 B) 13 C) 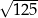 D)
D) 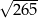
W kartezjańskim układzie współrzędnych 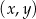 dane są: punkt
dane są: punkt 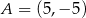 oraz okrąg o równaniu
oraz okrąg o równaniu 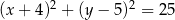 . Odległość punktu
. Odległość punktu 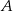 od środka tego okręgu jest równa
od środka tego okręgu jest równa
A) 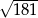 B) 3 C)
B) 3 C) 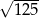 D)
D) 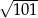
Ile jest okręgów o promieniu 1, które są jednocześnie styczne do prostej 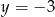 i okręgu
i okręgu 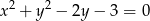 ?
?
A) 1 B) 2 C) 3 D) 4
Ile jest okręgów o promieniu 1, które są jednocześnie styczne do prostej 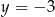 i wewnętrznie styczne do okręgu
i wewnętrznie styczne do okręgu 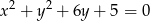 ?
?
A) 1 B) 2 C) 3 D) 4
Wskaż równanie prostej, która zawiera średnicę okręgu o równaniu 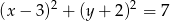 .
.
A) 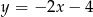 B)
B) 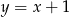 C)
C) 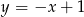 D)
D) 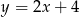
Wskaż równanie prostej, która zawiera średnicę okręgu o równaniu 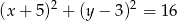 .
.
A) 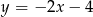 B)
B) 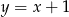 C)
C) 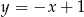 D)
D) 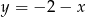
Dany jest okrąg o równaniu 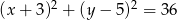 . Jedna ze średnic okręgu zawarta jest w prostej
. Jedna ze średnic okręgu zawarta jest w prostej
A) 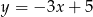 B)
B) 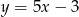 C)
C) 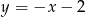 D)
D) 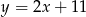
Promień okręgu o równaniu 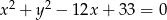 ma długość
ma długość
A) 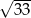 B)
B) 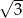 C) 3 D) 6
C) 3 D) 6
Promień okręgu danego równaniem 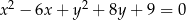 ma długość
ma długość
A) 2 B) 4 C) 9 D) 16
Promień okręgu danego równaniem 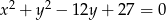 ma długość
ma długość
A) 3 B) 9 C) 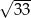 D)
D) 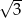
Promień okręgu danego równaniem 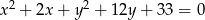 ma długość
ma długość
A) 2 B) 4 C) 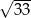 D)
D) 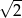
Promień okręgu danego równaniem 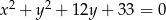 ma długość
ma długość
A) 3 B) 6 C) 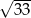 D)
D) 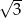
Okrąg o równaniu 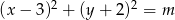 przechodzi przez punkt o współrzędnych
przechodzi przez punkt o współrzędnych 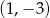 . Wtedy liczba
. Wtedy liczba 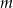 jest równa
jest równa
A) 25 B) 5 C) 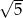 D) 17
D) 17
Okrąg o równaniu 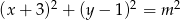 przechodzi przez punkt o współrzędnych
przechodzi przez punkt o współrzędnych 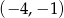 . Wtedy liczba
. Wtedy liczba 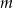 może być równa
może być równa
A) 25 B) 5 C) 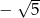 D)
D) 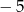
W ilu ćwiartkach układu współrzędnych znajdują się punkty okręgu o równaniu
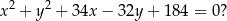
A) W jednej. B) W dwóch. C) W trzech. D) W czterech.
Prosta 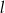 jest styczna do okręgu danego wzorem
jest styczna do okręgu danego wzorem 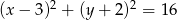 i równoległa do prostej
i równoległa do prostej 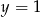 . Wskaż równanie prostej
. Wskaż równanie prostej 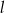
A)  B)
B) 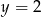 C)
C) 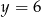 D)
D) 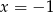
Prosta 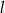 jest styczna do okręgu danego wzorem
jest styczna do okręgu danego wzorem 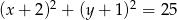 i równoległa do prostej
i równoległa do prostej 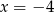 . Wskaż równanie prostej
. Wskaż równanie prostej 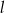
A) 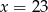 B)
B) 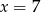 C)
C) 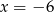 D)
D) 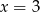
Prosta 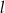 jest styczna do okręgu danego wzorem
jest styczna do okręgu danego wzorem 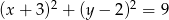 i równoległa do prostej
i równoległa do prostej 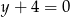 . Wskaż równanie prostej
. Wskaż równanie prostej 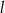
A) 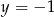 B)
B) 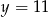 C)
C) 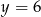 D)
D) 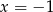
Okrąg o równaniu 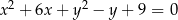 przekształcono w jednokładności o środku
przekształcono w jednokładności o środku 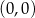 i skali
i skali 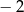 . Otrzymany okrąg ma równanie
. Otrzymany okrąg ma równanie
A) 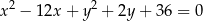 B)
B) 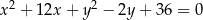
C) 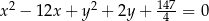 D)
D) 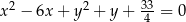
Okrąg 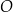 o środku
o środku 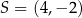 jest styczny do osi
jest styczny do osi 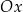 układu współrzędnych. Okrąg
układu współrzędnych. Okrąg 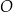 jest określony równaniem
jest określony równaniem
A) 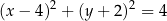 B)
B) 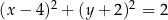
C) 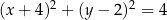 D)
D) 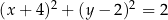
Okrąg 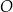 o środku
o środku 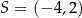 jest styczny do osi
jest styczny do osi 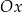 układu współrzędnych. Okrąg
układu współrzędnych. Okrąg 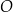 jest określony równaniem
jest określony równaniem
A) 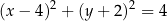 B)
B) 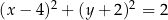
C) 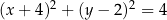 D)
D)