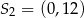Średnicą okręgu jest odcinek 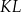 , gdzie
, gdzie 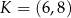 i
i 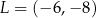 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 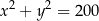 B)
B) 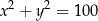 C)
C) 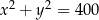 D)
D) 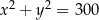
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Okrąg
W kartezjańskim układzie współrzędnych 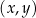 odcinek o końcach
odcinek o końcach 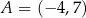 oraz
oraz 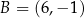 jest średnicą okręgu
jest średnicą okręgu 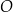 . Okrąg
. Okrąg 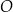 jest określony równaniem
jest określony równaniem
A) 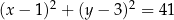 B)
B) 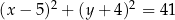
C) 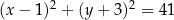 D)
D) 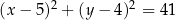
W kartezjańskim układzie współrzędnych 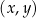 dane są cztery okręgi:
dane są cztery okręgi: 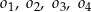 , o równaniach:
, o równaniach:
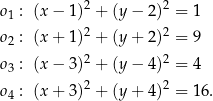
Okręgiem, który nie ma żadnego punktu wspólnego z osiami układu współrzędnych 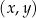 , jest
, jest
A) 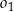 B)
B) 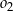 C)
C) 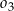 D)
D) 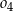
Okrąg o równaniu 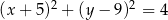 ma środek
ma środek 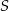 i promień
i promień  . Wówczas
. Wówczas
A) 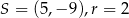 B)
B) 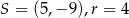
C) 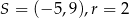 D)
D) 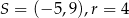
Okrąg o równaniu 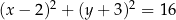 ma środek
ma środek 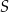 i promień
i promień  . Wówczas
. Wówczas
A) 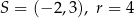 B)
B) 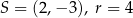
C) 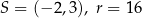 D)
D) 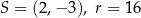
Okrąg o równaniu 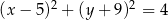 ma środek
ma środek 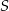 i promień
i promień  . Wówczas
. Wówczas
A) 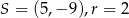 B)
B) 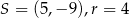
C) 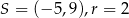 D)
D) 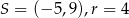
Okrąg o równaniu 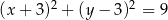 ma środek
ma środek 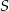 i promień
i promień  . Wówczas
. Wówczas
A) 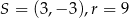 B)
B) 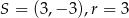
C) 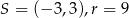 D)
D) 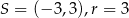
Wskaż równanie okręgu stycznego do prostej 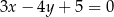 .
.
A) 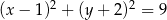 B)
B) 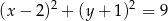
C) 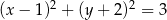 D)
D) 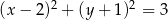
Wszystkie wierzchołki kwadratu 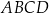 mają współrzędne nieujemne, przy czym
mają współrzędne nieujemne, przy czym 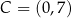 i
i 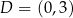 . Okrąg wpisany w kwadrat
. Okrąg wpisany w kwadrat 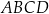 jest określony równaniem
jest określony równaniem
A) 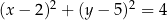 B)
B) 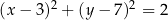
C) 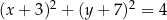 D)
D) 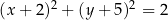
Okrąg o równaniu 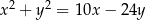 jest styczny do prostej
jest styczny do prostej
A) 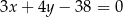 B)
B) 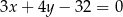 C)
C) 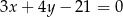 D)
D) 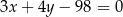
Ile punktów wspólnych ma prosta o równaniu 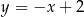 z okręgiem o środku w początku układu współrzędnych i promieniu 2?
z okręgiem o środku w początku układu współrzędnych i promieniu 2?
A) 0 B) 1 C) 2 D) 3
Ile punktów wspólnych ma prosta o równaniu 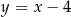 z okręgiem o środku w początku układu współrzędnych i promieniu 4?
z okręgiem o środku w początku układu współrzędnych i promieniu 4?
A) 3 B) 2 C) 1 D) 0
Punkty 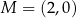 i
i 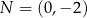 są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
A) 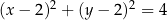 B)
B) 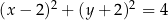
C) 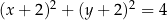 D)
D) 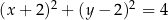
Punkty 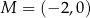 i
i 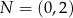 są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
A) 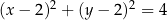 B)
B) 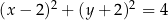
C) 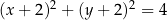 D)
D) 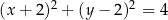
Okrąg o równaniu 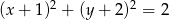 :
:
A) nie przecina osi 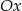 ,
,
B) nie przecina osi 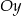 ,
,
C) przechodzi przez początek układu współrzędnych,
D) przechodzi przez punkt 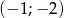 .
.
Okrąg o równaniu 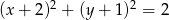 :
:
A) nie przecina osi 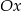 ,
,
B) nie przecina osi 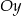 ,
,
C) przechodzi przez początek układu współrzędnych,
D) przechodzi przez punkt 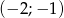 .
.
Promień okręgu o równaniu 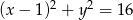 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Promień okręgu o równaniu 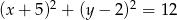 jest równy
jest równy
A) 12 B) 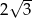 C)
C) 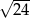 D) 144
D) 144
Promień okręgu o równaniu 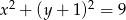 jest równy
jest równy
A) 1 B) 2 C) 3 D) 9
Promień okręgu o równaniu 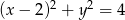 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Promień okręgu o równaniu 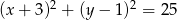 jest równy
jest równy
A) 25 B) 5 C) 625 D) 15
Promień okręgu o równaniu 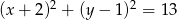 jest równy
jest równy
A) 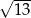 B) 13 C) 8 D)
B) 13 C) 8 D) 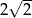
Punkty 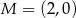 i
i 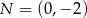 są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
A) 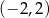 B)
B) 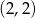 C)
C) 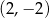 D)
D) 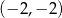
Punkty 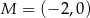 i
i 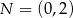 są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
A) 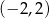 B)
B) 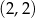 C)
C) 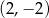 D)
D) 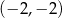
Na okręgu o równaniu 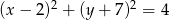 leży punkt
leży punkt
A) 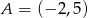 B)
B) 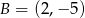 C)
C) 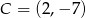 D)
D) 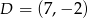
Na okręgu o równaniu 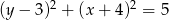 leży punkt
leży punkt
A) 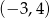 B)
B) 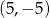 C)
C) 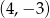 D)
D) 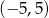
Do okręgu o równaniu 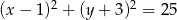 należy punkt
należy punkt
A) 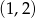 B)
B) 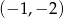 C)
C) 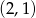 D)
D) 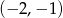
Punkt 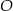 jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
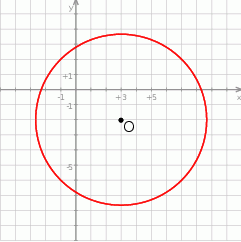
A) 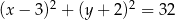 B)
B) 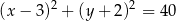
C) 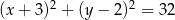 D)
D) 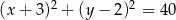
Ile punktów wspólnych ma prosta 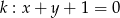 z okręgiem
z okręgiem 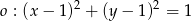 ?
?
A) 3 B) 2 C) 1 D) 0
Ile punktów wspólnych ma prosta 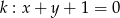 z okręgiem
z okręgiem 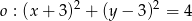 ?
?
A) 0 B) 1 C) 2 D) 3
Ile punktów wspólnych ma prosta 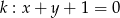 z okręgiem
z okręgiem 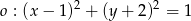 ?
?
A) 3 B) 2 C) 1 D) 0
Prosta 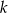 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 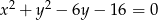 . Odległość środka tego okręgu od prostej
. Odległość środka tego okręgu od prostej 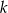 jest równa
jest równa
A) 9 B) 4 C) 25 D) 5
Prosta 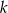 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 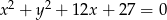 . Odległość środka tego okręgu od prostej
. Odległość środka tego okręgu od prostej 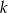 jest równa
jest równa
A) 9 B) 3 C) 25 D) 5
Wskaż równanie okręgu opisanego na trójkącie 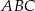 o wierzchołkach
o wierzchołkach 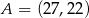 ,
, 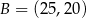 ,
, 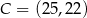
A) 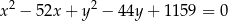 B)
B) 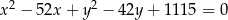
C) 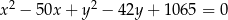 D)
D) 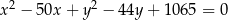
Okrąg o średnicy 6 jest styczny do osi 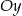 , a oś
, a oś 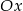 jest jego osią symetrii. Środek tego okręgu ma współrzędne
jest jego osią symetrii. Środek tego okręgu ma współrzędne
A) 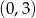 B)
B) 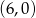 C)
C) 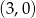 D)
D) 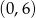
Środek 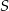 okręgu o równaniu
okręgu o równaniu 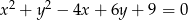 ma współrzędne
ma współrzędne
A) 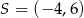 B)
B) 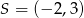 C)
C) 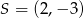 D)
D) 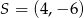
Środek okręgu o równaniu 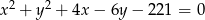 ma współrzędne
ma współrzędne
A) 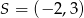 B)
B) 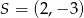 C)
C) 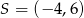 D)
D) 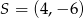
Środkiem okręgu o równaniu 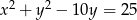 jest punkt
jest punkt
A) 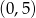 B)
B) 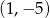 C)
C) 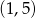 D)
D) 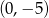
Środek 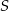 okręgu o równaniu
okręgu o równaniu 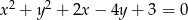 ma współrzędne
ma współrzędne
A) 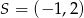 B)
B) 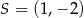 C)
C) 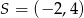 D)
D) 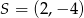
Środek 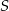 okręgu o równaniu
okręgu o równaniu 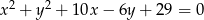 ma współrzędne
ma współrzędne
A) 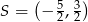 B)
B) 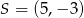 C)
C) 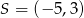 D)
D) 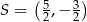
Środek 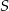 okręgu o równaniu
okręgu o równaniu 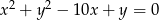 ma współrzędne
ma współrzędne
A) 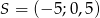 B)
B) 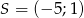 C)
C) 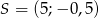 D)
D) 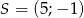
Środek 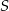 okręgu o równaniu
okręgu o równaniu 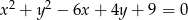 ma współrzędne
ma współrzędne
A) 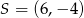 B)
B) 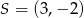 C)
C) 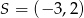 D)
D) 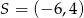
Odległość między środkami okręgów o równaniach 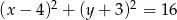 oraz
oraz 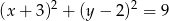 jest równa
jest równa
A) 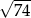 B)
B) 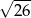 C)
C) 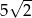 D)
D) 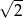
Okrąg o środku 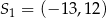 oraz okrąg o środku
oraz okrąg o środku 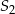 i promieniu 8 są styczne zewnętrznie w punkcie
i promieniu 8 są styczne zewnętrznie w punkcie 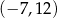 . Wtedy
. Wtedy
A) 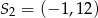 B)
B) 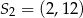 C)
C) 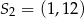 D)
D)