Do okręgu o środku 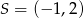 i promieniu
i promieniu 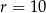 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 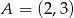 B)
B) 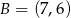 C)
C) 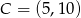 D)
D) 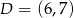
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Okrąg
Dany jest okrąg o środku 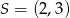 i promieniu
i promieniu 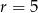 . Który z podanych punktów leży na tym okręgu?
. Który z podanych punktów leży na tym okręgu?
A) 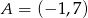 B)
B) 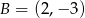 C)
C) 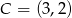 D)
D) 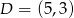
Dany jest okrąg o środku 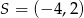 i promieniu
i promieniu 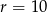 . Który z podanych punktów leży na tym okręgu?
. Który z podanych punktów leży na tym okręgu?
A) 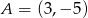 B)
B) 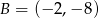 C)
C) 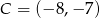 D)
D) 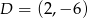
Do okręgu o środku 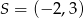 i promieniu
i promieniu 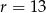 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 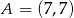 B)
B) 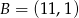 C)
C) 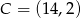 D)
D) 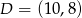
Okrąg o środku 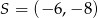 i promieniu 32 przekształcono najpierw w symetrii względem osi
i promieniu 32 przekształcono najpierw w symetrii względem osi 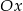 , a potem w symetrii względem osi
, a potem w symetrii względem osi 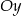 . W wyniku tych przekształceń otrzymano okrąg o środku
. W wyniku tych przekształceń otrzymano okrąg o środku 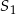 . Odległość między punktami
. Odległość między punktami 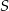 i
i 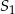 jest równa
jest równa
A) 20 B) 16 C) 10 D) 64
Dany jest okrąg o środku 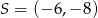 i promieniu 2014. Obrazem tego okręgu w symetrii osiowej względem osi
i promieniu 2014. Obrazem tego okręgu w symetrii osiowej względem osi 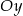 jest okrąg o środku w punkcie
jest okrąg o środku w punkcie 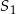 . Odległość między punktami
. Odległość między punktami 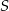 i
i 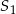 jest równa
jest równa
A) 12 B) 16 C) 2014 D) 4028
Dany jest okrąg o środku 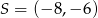 i promieniu 2015. Obrazem tego okręgu w symetrii osiowej względem osi
i promieniu 2015. Obrazem tego okręgu w symetrii osiowej względem osi 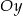 jest okrąg o środku w punkcie
jest okrąg o środku w punkcie 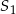 . Odległość między punktami
. Odległość między punktami 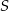 i
i 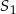 jest równa
jest równa
A) 12 B) 16 C) 2015 D) 4030
Okręgi o środkach 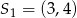 oraz
oraz 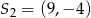 i równych promieniach są styczne zewnętrznie. Promień każdego z tych okręgów jest równy
i równych promieniach są styczne zewnętrznie. Promień każdego z tych okręgów jest równy
A) 8 B) 6 C) 5 D) 
Okrąg o środku 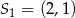 i promieniu
i promieniu  oraz okrąg o środku
oraz okrąg o środku 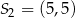 i promieniu 4 są styczne zewnętrznie. Wtedy
i promieniu 4 są styczne zewnętrznie. Wtedy
A) 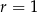 B)
B) 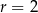 C)
C) 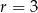 D)
D) 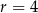
Okręgi o środkach 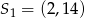 oraz
oraz 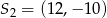 i równych promieniach są styczne zewnętrznie. Promień każdego z tych okręgów jest równy
i równych promieniach są styczne zewnętrznie. Promień każdego z tych okręgów jest równy
A) 26 B) 13 C) 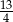 D)
D) 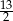
W kartezjańskim układzie współrzędnych 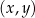 dany jest okrąg
dany jest okrąg  o równaniu
o równaniu
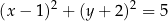
Do okręgu  należy punkt o współrzędnych należy punkt o współrzędnych 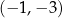 . . | P | F |
Promień okręgu 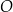 jest równy 5. jest równy 5. | P | F |
Punkt 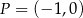 leży na okręgu o promieniu 3. Równanie tego okręgu może mieć postać
leży na okręgu o promieniu 3. Równanie tego okręgu może mieć postać
A) 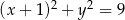 B)
B) 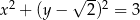
C) 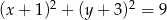 D)
D) 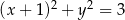
Na płaszczyźnie, w kartezjańskim układzie współrzędnych  , dany jest okrąg
, dany jest okrąg  o równaniu
o równaniu
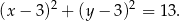
Okrąg  przecina oś
przecina oś  w punktach o współrzędnych
w punktach o współrzędnych
A) 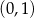 i
i 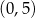 B)
B) 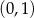 i
i 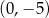
C) 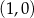 i
i 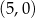 D)
D) 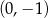 i
i 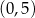
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 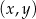 , dany jest okrąg
, dany jest okrąg  o równaniu
o równaniu
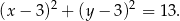
Okrąg  przecina oś
przecina oś 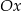 w punktach o współrzędnych
w punktach o współrzędnych
A) 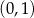 i
i 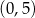 B)
B) 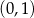 i
i 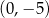
C) 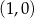 i
i 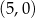 D)
D) 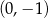 i
i 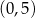
Okrąg o równaniu 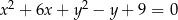 przesunięto o wektor
przesunięto o wektor ![[ 13] 9,− 2](https://img.zadania.info/zad/5991873/HzadT1x.gif) . Środek otrzymanego w ten sposób okręgu ma współrzędne
. Środek otrzymanego w ten sposób okręgu ma współrzędne
A) 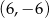 B)
B) 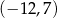 C)
C) 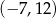 D)
D) 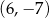
Wskaż równanie okręgu o promieniu 6.
A) 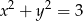 B)
B) 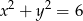 C)
C) 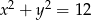 D)
D) 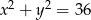
Wskaż równanie okręgu o promieniu 9.
A) 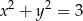 B)
B) 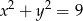 C)
C) 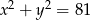 D)
D) 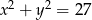
Wskaż równanie okręgu o promieniu 4.
A) 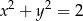 B)
B) 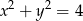 C)
C) 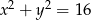 D)
D) 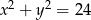
Okręgi 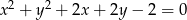 oraz
oraz 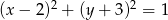
A) są styczne zewnętrznie B) są styczne wewnętrznie C) są rozłączne D) przecinają się
Okrąg 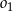 ma równanie
ma równanie 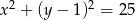 , a okrąg
, a okrąg 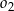 ma równanie
ma równanie 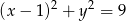 . Określ wzajemne położenie tych okręgów.
. Określ wzajemne położenie tych okręgów.
A) Te okręgi przecinają się w dwóch punktach.
B) Te okręgi są styczne.
C) Te okręgi nie mają punktów wspólnych oraz okrąg 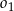 leży w całości wewnątrz okręgu
leży w całości wewnątrz okręgu 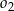 .
.
D) Te okręgi nie mają punktów wspólnych oraz okrąg 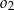 leży w całości wewnątrz okręgu
leży w całości wewnątrz okręgu 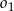 .
.
Okrąg 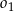 ma równanie
ma równanie 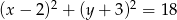 , a okrąg
, a okrąg 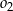 ma równanie
ma równanie 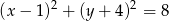 . Określ wzajemne położenie tych okręgów.
. Określ wzajemne położenie tych okręgów.
A) Te okręgi przecinają się w dwóch punktach.
B) Te okręgi są styczne.
C) Te okręgi nie mają punktów wspólnych oraz okrąg 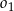 leży w całości wewnątrz okręgu
leży w całości wewnątrz okręgu 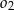 .
.
D) Te okręgi nie mają punktów wspólnych oraz okrąg 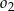 leży w całości wewnątrz okręgu
leży w całości wewnątrz okręgu 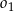 .
.
Środek okręgu o równaniu 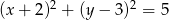 ma współrzędne:
ma współrzędne:
A) 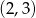 B)
B) 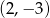 C)
C) 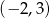 D)
D) 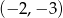
Dany jest okrąg o równaniu 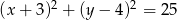 . Środkiem
. Środkiem 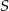 tego okręgu jest punkt:
tego okręgu jest punkt:
A) 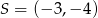 B)
B) 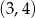 C)
C) 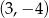 D)
D) 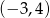
Dany jest okrąg o równaniu 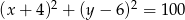 . Środek tego okręgu ma współrzędne
. Środek tego okręgu ma współrzędne
A) 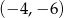 B)
B) 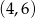 C)
C) 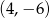 D)
D) 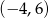
Wskaż równanie okręgu stycznego do osi 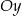 .
.
A) 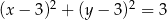 B)
B) 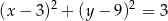
C) 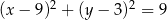 D)
D) 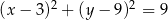
Okrąg o równaniu 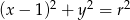 , gdzie
, gdzie 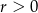 , ma z prostą
, ma z prostą 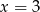 dwa punkty wspólne. Zatem
dwa punkty wspólne. Zatem
A) 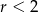 B)
B) 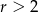 C)
C) 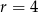 D)
D) 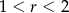
Okrąg o równaniu 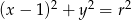 , gdzie
, gdzie 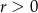 , nie przecina prostej
, nie przecina prostej 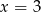 . Zatem
. Zatem
A) 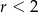 B)
B) 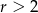 C)
C) 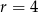 D)
D) 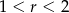
Okrąg o równaniu 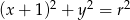 , gdzie
, gdzie 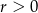 , ma z prostą
, ma z prostą 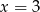 dwa punkty wspólne. Zatem
dwa punkty wspólne. Zatem
A) 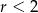 B)
B) 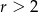 C)
C) 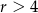 D)
D) 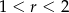
Okrąg o równaniu 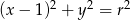 , gdzie
, gdzie 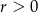 , ma z prostą
, ma z prostą 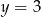 dwa punkty wspólne. Zatem
dwa punkty wspólne. Zatem
A) 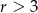 B)
B) 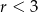 C)
C) 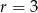 D)
D) 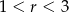
W układzie współrzędnych 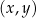 odcinek o końcach
odcinek o końcach 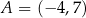 oraz
oraz 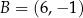 jest średnicą okręgu
jest średnicą okręgu 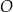 . Środkiem okręgu
. Środkiem okręgu 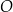 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 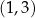 B)
B) 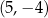 C)
C) 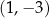 D)
D) 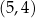
Punkt 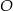 jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
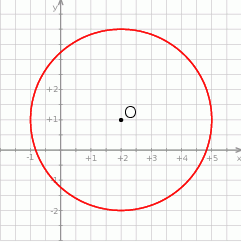
A) 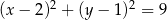 B)
B) 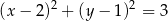
C) 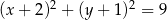 D)
D) 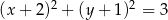
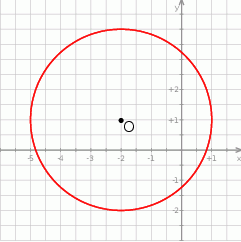
Punkt  jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
A) 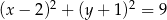 B)
B) 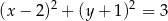
C) 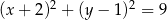 D)
D) 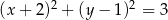
Okrąg 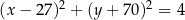 jest styczny do prostej
jest styczny do prostej
A) 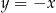 B)
B) 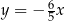 C)
C) 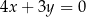 D)
D) 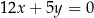
Okrąg 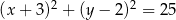 jest styczny do prostej
jest styczny do prostej
A) 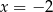 B)
B) 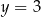 C)
C) 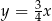 D)
D) 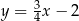
Okrąg 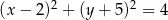 jest styczny do prostej
jest styczny do prostej
A) 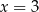 B)
B) 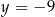 C)
C) 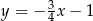 D)
D) 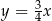
Liczba punktów wspólnych okręgu o równaniu 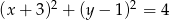 z osiami układu współrzędnych jest równa
z osiami układu współrzędnych jest równa
A) 0 B) 1 C) 2 D) 4
Liczba punktów wspólnych okręgu o równaniu 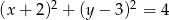 z osiami układu współrzędnych jest równa
z osiami układu współrzędnych jest równa
A) 0 B) 1 C) 2 D) 4
Liczba punktów wspólnych okręgu o równaniu 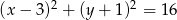 z osiami układu współrzędnych jest równa
z osiami układu współrzędnych jest równa
A) 0 B) 1 C) 2 D) 4
Styczną do okręgu 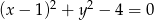 jest prosta o równaniu
jest prosta o równaniu
A) 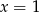 B)
B) 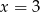 C)
C) 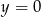 D)
D) 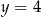
Styczną do okręgu 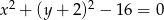 jest prosta o równaniu
jest prosta o równaniu
A) 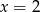 B)
B) 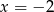 C)
C) 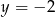 D)
D) 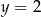
Dany jest okrąg 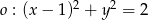 i prosta
i prosta 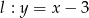 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Prosta 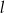 przechodzi przez środek okręgu.
przechodzi przez środek okręgu.
B) Prosta 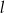 jest rozłączna z okręgiem.
jest rozłączna z okręgiem.
C) Prosta 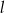 jest styczna do okręgu.
jest styczna do okręgu.
D) Prosta 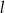 ma z okręgiem dwa punkty wspólne.
ma z okręgiem dwa punkty wspólne.
Dany jest okrąg 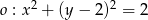 i prosta
i prosta 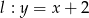 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Prosta 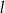 jest rozłączna z okręgiem.
jest rozłączna z okręgiem.
B) Prosta 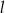 przechodzi przez środek okręgu.
przechodzi przez środek okręgu.
C) Prosta 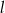 jest styczna do okręgu.
jest styczna do okręgu.
D) Prosta 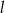 ma z okręgiem jeden punkt wspólny.
ma z okręgiem jeden punkt wspólny.

