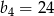Suma 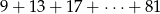 kolejnych wyrazów ciągu arytmetycznego jest równa
kolejnych wyrazów ciągu arytmetycznego jest równa
A) 859 B) 851 C) 855 D) 1710
/Szkoła średnia/Zadania testowe/Ciągi
Suma 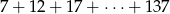 kolejnych wyrazów ciągu arytmetycznego jest równa
kolejnych wyrazów ciągu arytmetycznego jest równa
A) 3888 B) 1944 C) 2016 D) 1800
W ciągu geometrycznym drugi wyraz jest równy 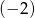 , a trzeci wyraz
, a trzeci wyraz 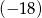 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -9 B) -3 C) 3 D) 9
W ciągu geometrycznym drugi wyraz jest równy 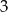 , a trzeci wyraz
, a trzeci wyraz 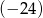 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -8 B) -4 C) 4 D) 8
W ciągu geometrycznym piąty wyraz jest równy  , a szósty wyraz jest równy
, a szósty wyraz jest równy 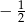 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A)  B)
B)  C)
C) 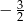 D)
D) 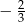
Dany jest ciąg arytmetyczny 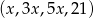 . Wtedy
. Wtedy
A) 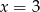 B)
B) 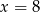 C)
C) 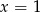 D)
D) 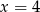
Dany jest ciąg arytmetyczny 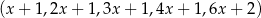 . Wtedy
. Wtedy
A) 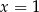 B)
B) 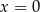 C)
C) 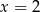 D)
D) 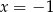
Szereg geometryczny:
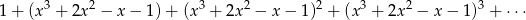
jest zbieżny dla
A) 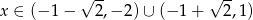
B) 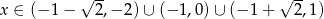
C) 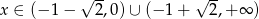
D) 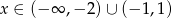
W ciągu arytmetycznym 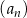 , określonym dla
, określonym dla 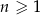 , spełniony jest warunek
, spełniony jest warunek 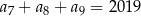 . Suma
. Suma 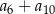 jest równa
jest równa
A) 673 B) 1346 C) 1009,5 D) 2019
Pierwszy wyraz ciągu arytmetycznego jest równy 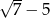 , a drugi wyraz jest równy
, a drugi wyraz jest równy 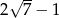 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 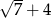 B)
B) 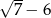 C)
C) 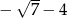 D)
D) 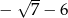
Pierwszy wyraz ciągu arytmetycznego jest równy 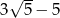 , a drugi wyraz jest równy
, a drugi wyraz jest równy 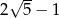 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 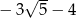 B)
B) 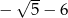 C)
C) 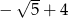 D)
D) 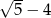
Pierwszy wyraz ciągu arytmetycznego jest równy 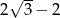 , a drugi wyraz jest równy
, a drugi wyraz jest równy 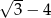 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 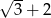 B)
B) 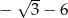 C)
C) 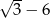 D)
D) 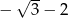
Ciąg 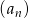 określony jest wzorem
określony jest wzorem 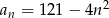 , gdzie
, gdzie 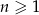 . Liczba nieujemnych wyrazów tego ciągu jest równa
. Liczba nieujemnych wyrazów tego ciągu jest równa
A) 11 B) 22 C) 10 D) 5
Ciąg 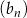 jest określony wzorem
jest określony wzorem 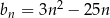 dla każdej liczby naturalnej
dla każdej liczby naturalnej 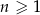 . Liczba niedodatnich wyrazów ciągu
. Liczba niedodatnich wyrazów ciągu 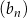 jest równa
jest równa
A) 14 B) 13 C) 9 D) 8
Ciąg 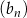 jest określony wzorem
jest określony wzorem 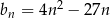 dla każdej liczby naturalnej
dla każdej liczby naturalnej 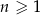 . Liczba niedodatnich wyrazów ciągu
. Liczba niedodatnich wyrazów ciągu 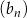 jest równa
jest równa
A) 6 B) 12 C) 9 D) 8
Ciąg 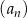 jest określony wzorem
jest określony wzorem 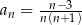 dla każdej liczby naturalnej
dla każdej liczby naturalnej 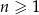 . Wynika stąd, że suma siedmiu początkowych wyrazów ciągu
. Wynika stąd, że suma siedmiu początkowych wyrazów ciągu 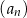 jest większa od sumy pięciu początkowych wyrazów ciągu
jest większa od sumy pięciu początkowych wyrazów ciągu 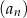 o
o
A)  B)
B) 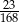 C)
C) 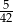 D) 0
D) 0
Granice 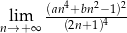 i
i 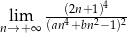 są równe. Stąd wynika, że
są równe. Stąd wynika, że
A) 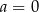 i
i 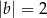 B)
B) 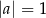 i
i 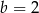 C)
C) 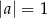 i
i 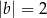 D)
D) 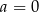 i
i 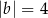
Iloraz ciągu geometrycznego 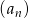 o wyrazie ogólnym
o wyrazie ogólnym 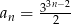 jest równy
jest równy
A) 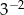 B)
B) 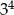 C)
C) 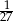 D) 27
D) 27
Ciąg geometryczny 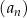 jest określony wzorem
jest określony wzorem 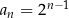 , dla każdej liczby naturalnej
, dla każdej liczby naturalnej 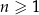 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 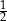 B)
B) 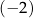 C) 2 D) 1
C) 2 D) 1
Ciąg geometryczny 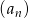 określony jest wzorem
określony jest wzorem 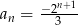 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 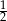 B)
B) 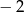 C)
C) 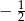 D) 2
D) 2
Ciąg geometryczny 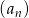 określony jest wzorem
określony jest wzorem 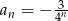 dla
dla 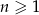 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 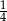 B)
B) 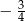 C)
C)  D)
D) 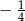
Ciąg geometryczny 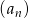 określony jest wzorem
określony jest wzorem 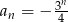 dla
dla 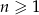 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 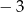 B)
B) 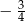 C)
C)  D) 3
D) 3
Iloraz ciągu geometrycznego 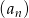 o wyrazie ogólnym
o wyrazie ogólnym 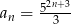 jest równy
jest równy
A) 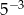 B)
B) 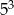 C) 25 D)
C) 25 D) 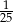
Wzór ogólny ciągu 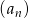 ma postać
ma postać 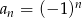 , dla
, dla 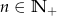 . Zatem ciąg ten jest
. Zatem ciąg ten jest
A) arytmetyczny B) geometryczny C) malejący D) rosnący
Ciąg 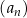 , określony wzorem
, określony wzorem 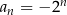 dla każdej liczby naturalnej
dla każdej liczby naturalnej 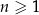 , jest
, jest
A) ciągiem arytmetycznym o różnicy 2.
B) ciągiem arytmetycznym o różnicy 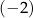 .
.
C) ciągiem geometrycznym o ilorazie 2.
D) ciągiem geometrycznym o ilorazie 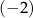 .
.
Wzór ogólny ciągu 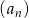 ma postać
ma postać 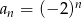 , dla
, dla 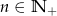 . Zatem ciąg ten jest
. Zatem ciąg ten jest
A) arytmetyczny B) malejący C) geometryczny D) rosnący
Ciąg 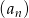 określony jest wzorem
określony jest wzorem 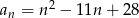 , gdzie
, gdzie 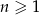 . Liczba niedodatnich wyrazów tego ciągu jest równa
. Liczba niedodatnich wyrazów tego ciągu jest równa
A) 2 B) 3 C) 4 D) 7
Ciąg 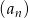 określony jest wzorem
określony jest wzorem 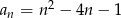 , gdzie
, gdzie 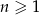 . Liczba ujemnych wyrazów tego ciągu jest równa
. Liczba ujemnych wyrazów tego ciągu jest równa
A) 2 B) 3 C) 4 D) 5
W ciągu arytmetycznym 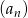 dla dwóch różnych liczb naturalnych
dla dwóch różnych liczb naturalnych 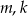 mamy:
mamy: 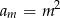 oraz
oraz 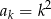 . Z tego wynika, że różnica ciągu
. Z tego wynika, że różnica ciągu 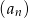 jest równa:
jest równa:
A) 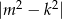 B)
B) 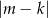 C)
C) 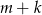 D)
D) 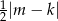
Dany jest rosnący ciąg 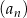 określony dla
określony dla 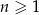 , którego wyrazami są wszystkie liczby trzycyfrowe podzielne przez 17. Dziewiętnasty wyraz tego ciągu jest równy
, którego wyrazami są wszystkie liczby trzycyfrowe podzielne przez 17. Dziewiętnasty wyraz tego ciągu jest równy
A) 425 B) 323 C) 408 D) 493
Czterowyrazowy ciąg 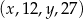 jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
A) 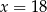 B)
B) 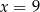 C)
C) 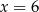 D)
D) 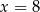
Wiadomo, że liczba 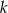 jest liczbą naturalną dodatnią i liczby
jest liczbą naturalną dodatnią i liczby 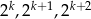 są trzema początkowymi wyrazami ciągu geometrycznego
są trzema początkowymi wyrazami ciągu geometrycznego 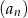 , gdzie
, gdzie 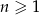 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 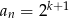 B)
B) 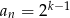 C)
C) 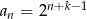 D)
D) 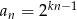
Wiadomo, że liczba 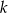 jest liczbą naturalną dodatnią i liczby
jest liczbą naturalną dodatnią i liczby 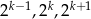 są trzema początkowymi wyrazami ciągu geometrycznego
są trzema początkowymi wyrazami ciągu geometrycznego 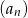 , gdzie
, gdzie 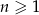 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 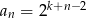 B)
B) 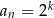 C)
C) 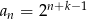 D)
D) 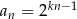
Wiadomo, że liczba 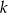 jest liczbą naturalną dodatnią i liczby
jest liczbą naturalną dodatnią i liczby 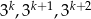 są trzema początkowymi wyrazami ciągu geometrycznego
są trzema początkowymi wyrazami ciągu geometrycznego 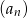 , gdzie
, gdzie 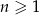 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 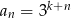 B)
B) 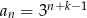 C)
C) 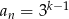 D)
D) 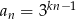
Pierwszy wyraz ciągu arytmetycznego jest równy 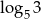 , a drugi wyraz
, a drugi wyraz 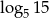 . Różnica tego ciągu to liczba
. Różnica tego ciągu to liczba
A) 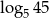 B)
B) 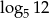 C) 1 D) 12
C) 1 D) 12
Pierwszy wyraz ciągu arytmetycznego jest równy 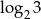 , a drugi wyraz
, a drugi wyraz 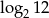 . Różnica tego ciągu to liczba
. Różnica tego ciągu to liczba
A) 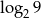 B) 2 C)
B) 2 C) 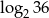 D) -2
D) -2
Pierwszy wyraz ciągu arytmetycznego jest równy 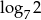 , a drugi wyraz
, a drugi wyraz 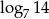 . Różnica tego ciągu to liczba
. Różnica tego ciągu to liczba
A) 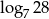 B) 1 C)
B) 1 C) 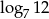 D) 7
D) 7
Liczby 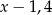 i 8 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Wówczas liczba
i 8 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Wówczas liczba  jest równa
jest równa
A) 3 B) 1 C) -1 D) -7
Liczby 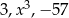 tworzą w podanej kolejności ciąg arytmetyczny. Liczba
tworzą w podanej kolejności ciąg arytmetyczny. Liczba  jest równa
jest równa
A) 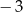 B) 3 C)
B) 3 C) 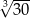 D)
D) 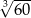
Liczby: 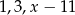 , w podanej kolejności, są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Liczba
, w podanej kolejności, są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Liczba  jest równa
jest równa
A) 5 B) 9 C) 16 D) 20
Dany jest ciąg liczbowy 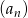 , w którym
, w którym 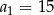 ,
, 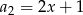 ,
, 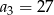 . Dla jakiej wartości liczbowej
. Dla jakiej wartości liczbowej  dany ciąg jest ciągiem arytmetycznym?
dany ciąg jest ciągiem arytmetycznym?
A) 8 B) 9 C) 10 D) 11
Liczby: 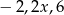 w podanej kolejności tworzą ciąg arytmetyczny. Zatem liczba
w podanej kolejności tworzą ciąg arytmetyczny. Zatem liczba  jest równa
jest równa
A) 4 B) 1 C) -1 D) 2
Trzywyrazowy ciąg 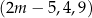 jest arytmetyczny. Liczba
jest arytmetyczny. Liczba 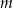 jest równa
jest równa
A) 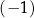 B) 2 C) 3 D)
B) 2 C) 3 D) 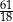
Liczby 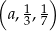 tworzą ciąg arytmetyczny, zatem
tworzą ciąg arytmetyczny, zatem
A) 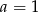 B)
B) 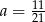 C)
C) 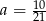 D)
D) 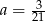
Trzywyrazowy ciąg 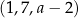 jest arytmetyczny. Liczba
jest arytmetyczny. Liczba  jest równa
jest równa
A) 49 B) 15 C) 13 D) 6
Liczby 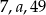 w podanej kolejności tworzą ciąg arytmetyczny. Wtedy
w podanej kolejności tworzą ciąg arytmetyczny. Wtedy  jest równe
jest równe
A) 14 B) 21 C) 28 D) 42
Trzywyrazowy ciąg 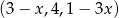 jest ciągiem arytmetycznym wtedy i tylko wtedy, gdy:
jest ciągiem arytmetycznym wtedy i tylko wtedy, gdy:
A) 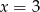 B)
B) 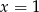 C)
C) 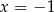 D)
D) 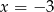
Trzywyrazowy ciąg 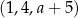 jest arytmetyczny. Liczba
jest arytmetyczny. Liczba  jest równa
jest równa
A) 0 B) 7 C) 2 D) 11
Ciąg geometryczny 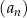 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 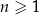 . W tym ciągu
. W tym ciągu 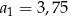 oraz
oraz 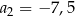 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 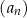 jest równa
jest równa
A) 11,25 B) 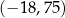 C) 15 D)
C) 15 D) 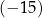
Ciąg geometryczny 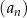 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 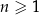 . W tym ciągu
. W tym ciągu 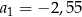 oraz
oraz 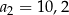 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 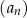 jest równa
jest równa
A) 48,45 B) 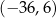 C) 7,65 D)
C) 7,65 D) 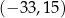
W ciągu geometrycznym 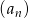 dane są:
dane są: 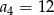 i
i 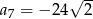 . Ciąg geometryczny
. Ciąg geometryczny 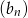 ma taki sam pierwszy wyraz jak ciąg
ma taki sam pierwszy wyraz jak ciąg 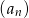 , ale jego iloraz jest dwukrotnością ilorazu ciągu
, ale jego iloraz jest dwukrotnością ilorazu ciągu 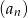 . Zatem
. Zatem
A) 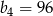 B)
B) 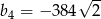 C)
C) 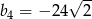 D)
D)