Mediana niemalejącego zestawu danych 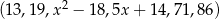 jest równa 40. Zatem
jest równa 40. Zatem
A) istnieją więcej niż dwie możliwe wartości liczby  .
.
B) istnieją dokładnie dwie możliwe wartości liczby  .
.
C) istnieje dokładnie jedna możliwa wartość liczby  .
.
D) nie istnieje liczba  spełniająca podany warunek.
spełniająca podany warunek.
/Szkoła średnia/Zadania testowe/Statystyka
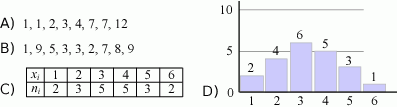
Dla której z przedstawionych serii danych mediana jest równa 3?
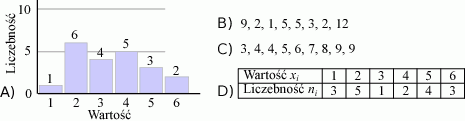
Dla której z przedstawionych serii danych mediana jest równa 4?
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 1 | 4 | 3 | 5 | 4 | 3 |
Średnia liczba oczek otrzymana w jednym rzucie jest równa.
A) 4 B) 3,8 C) 3,5 D) 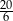
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 5 | 3 | 4 | 1 | 5 | 2 |
Średnia liczba oczek otrzymana w jednym rzucie jest równa.
A) 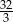 B) 3,5 C) 3,2 D)
B) 3,5 C) 3,2 D) 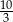
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
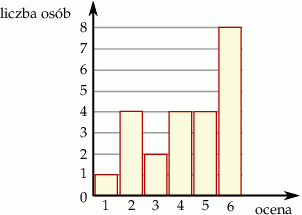
Mediana ocen uzyskanych przez uczniów jest równa
A) 6 B) 5 C) 4,5 D) 4
Przeprowadzono badanie dotyczące liczby samochodów osobowych w rodzinie. Wyniki przedstawia poniższy diagram
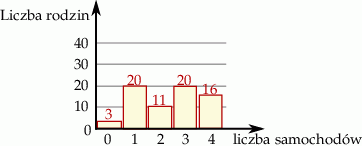
Mediana liczby samochodów w rodzinie wynosi
A) 2 B) 2,5 C) 3 D) 3,5
Na diagramie przedstawiono wyniki sprawdzianu z matematyki w pewnej klasie maturalnej. Na osi poziomej podano oceny, które uzyskali uczniowie tej klasy, a na osi pionowej podano liczbę uczniów, którzy otrzymali daną ocenę.
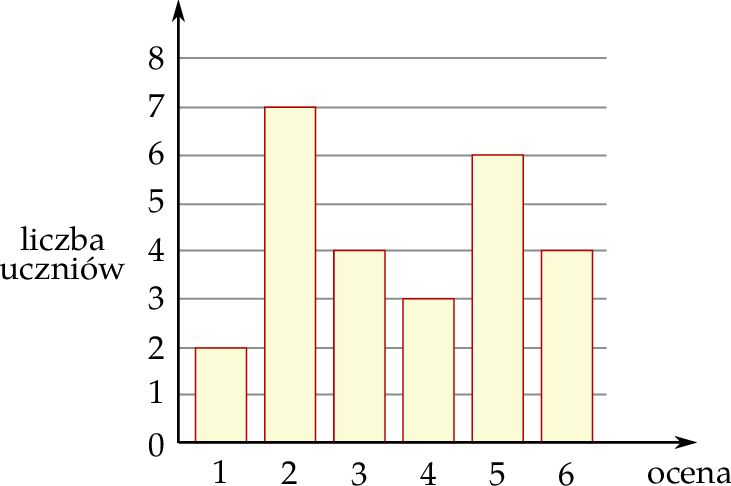
Mediana ocen uzyskanych z tego sprawdzianu przez uczniów tej klasy jest równa
A) 4,5 B) 4 C) 3,5 D) 3
Przeprowadzono badanie dotyczące liczby samochodów osobowych w rodzinie. Wyniki przedstawia poniższy diagram
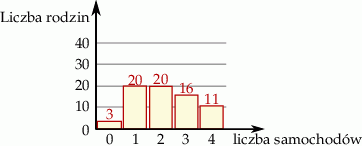
Mediana liczby samochodów w rodzinie wynosi
A) 2 B) 2,5 C) 3 D) 3,5
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
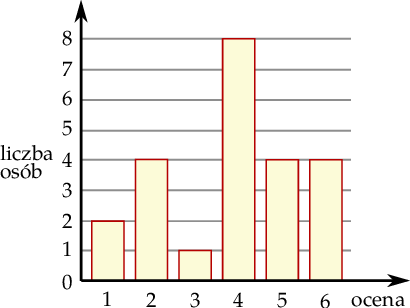
Mediana ocen uzyskanych przez uczniów jest równa
A) 3,5 B) 5 C) 4,5 D) 4
Poniższy diagram przedstawia wiek uczestników pewnej wycieczki.
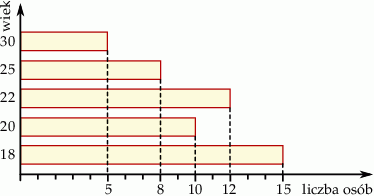
Mediana wieku osób uczestniczących w tej wycieczce jest równa:
A) 21 lat B) 21,68 lat C) 22 lata D) 23 lata
Firma  zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy
zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy  , którzy otrzymują płacę miesięczną w danej wysokości.
, którzy otrzymują płacę miesięczną w danej wysokości.
Mediana miesięcznej płacy pracowników firmy 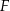 jest równa
jest równa
A) 4 000 zł B) 4 800 zł C) 5 000 zł D) 5 500 zł
Poniższy diagram przedstawia wiek uczestników pewnej wycieczki.
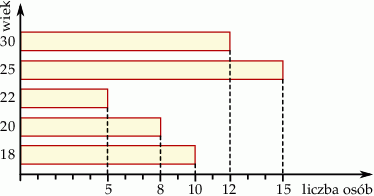
Mediana wieku osób uczestniczących w tej wycieczce jest równa:
A) 21 lat B) 22 lata C) 23,5 lat D) 25 lat
Na diagramie podano wzrost uczniów klasy I w pewnym liceum.
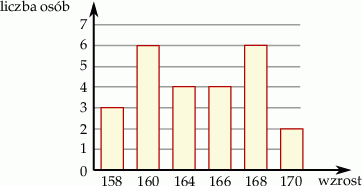
Mediana wszystkich wyników jest równa
A) 163 B) 164 C) 165 D) 166
Ania otrzymała z pięciu sprawdzianów z matematyki następujące oceny: 5, 2, 3, 2, 5. Po kolejnych dwóch sprawdzianach średnia ocen Ani ze wszystkich sprawdzianów wyniosła 4. Jakie oceny mogła otrzymać Ania z ostatnich dwóch sprawdzianów?
A) 4 i 5 B) 5 i 5 C) 6 i 6 D) 5 i 6
Tomek otrzymał z sześciu sprawdzianów z matematyki następujące oceny: 5, 4, 2, 3, 2, 3. Po kolejnych dwóch sprawdzianach średnia ocen Tomka ze wszystkich sprawdzianów wyniosła 3,5. Jakie oceny mógł otrzymać Tomek z ostatnich dwóch sprawdzianów?
A) 4 i 4 B) 4 i 5 C) 3 i 4 D) 5 i 3
Średnia arytmetyczna zestawu danych:
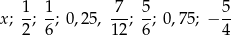
jest równa 0,25. Wtedy mediana tego zestawu danych jest równa
A) 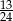 B)
B) 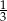 C)
C)  D)
D) 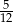
W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [19 dag, 21 dag]. Pobrano próbę kontrolną liczącą 50 jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie.
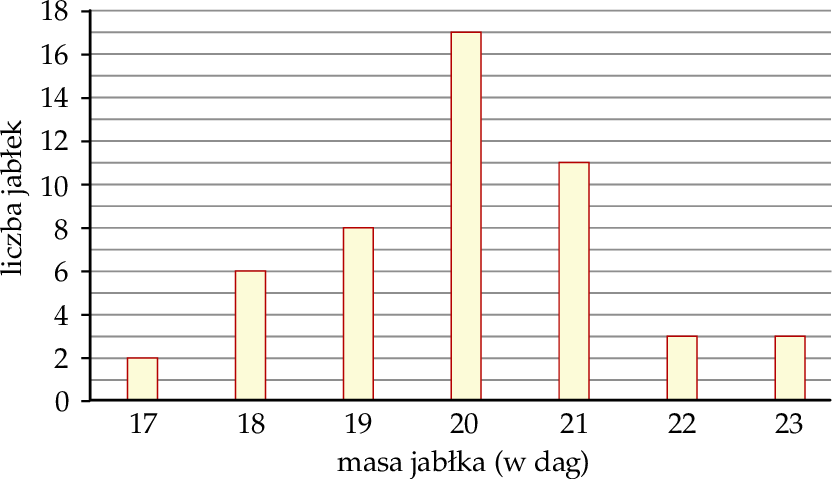
Dominanta masy 50 zważonych jabłek (w zaokrągleniu do pełnych dekagramów) z pobranej próby kontrolnej jest równa
| A) 20 dag, | B) 23 dag, |
ponieważ
| 1) | ta masa jest największa w tej próbie. |
| 2) | iloczyn tej masy i liczby jabłek o takiej masie jest największy w tej próbie. |
| 3) | ta masa występuje najliczniej w tej próbie. |
W hurtowni owoców wyselekcjonowana gruszka spełnia normę jakości, gdy jej masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [16 dag, 18 dag]. Pobrano próbę kontrolną liczącą 50 gruszek i następnie zważono każdą z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy gruszek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę gruszki (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę gruszek o określonej masie.
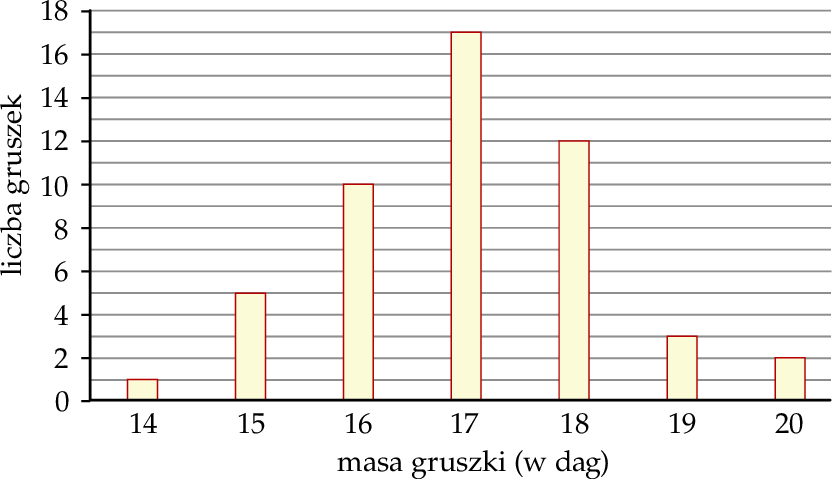
Dominanta masy 50 zważonych gruszek (w zaokrągleniu do pełnych dekagramów) z pobranej próby kontrolnej jest równa
| A) 18 dag, | B) 17 dag, |
ponieważ
| 1) | ta masa jest największa w tej próbie. |
| 3) | ta masa występuje najliczniej w tej próbie. |
| 3) | iloczyn tej masy i liczby gruszek o takiej masie jest największy w tej próbie. |
Na wykresie słupkowym poniżej podano rozkład miesięcznych zarobków wszystkich pracowników w pewnej firmie  . Na osi poziomej podano – wyrażone w tysiącach złotych – miesięczne wynagrodzenie netto pracowników firmy
. Na osi poziomej podano – wyrażone w tysiącach złotych – miesięczne wynagrodzenie netto pracowników firmy  , a na osi pionowej przedstawiono liczbę osób, która osiąga podane zarobki.
, a na osi pionowej przedstawiono liczbę osób, która osiąga podane zarobki.
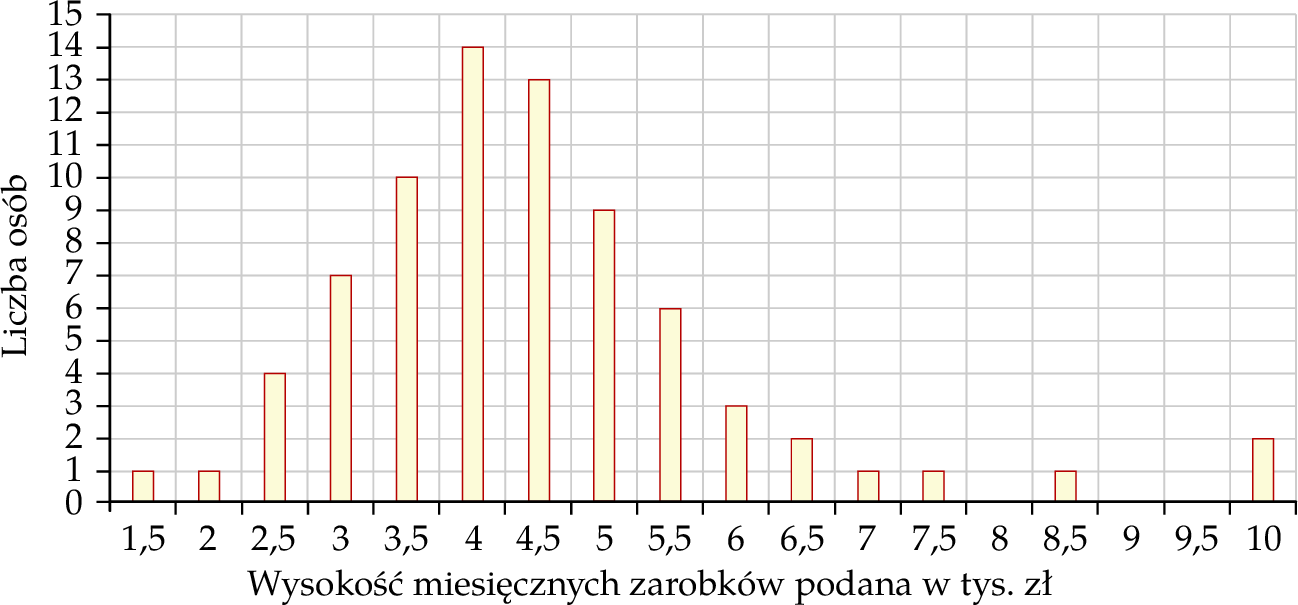
Dominantą miesięcznych zarobków w firmie  jest
jest
| A) 10 tys. zł, | B) 4,5 tys. zł, | C) 4 tys. zł, |
ponieważ
| 1) | tę wartość zarobków osiąga najwięcej osób w firmie  . . |
| 2) | ta wartość zarobków jest największa w firmie  . . |
| 3) | iloczyn tej wartości zarobków i liczby osób z takimi zarobkami jest największy w firmie  . . |
W zestawie 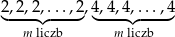 jest
jest 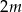 liczb (
liczb (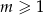 ), w tym
), w tym 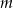 liczb 2 i
liczb 2 i 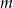 liczb 4. Odchylenie standardowe tego zestawu liczb jest równe
liczb 4. Odchylenie standardowe tego zestawu liczb jest równe
A) 2 B) 1 C) 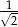 D)
D) 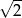
W zestawie 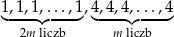 jest
jest 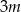 liczb (
liczb (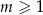 ), w tym
), w tym 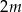 liczb 1 i
liczb 1 i 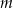 liczb 4. Odchylenie standardowe tego zestawu liczb jest równe
liczb 4. Odchylenie standardowe tego zestawu liczb jest równe
A) 2 B) 1 C) 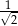 D)
D) 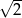
W zestawie 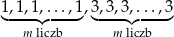 jest
jest 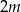 liczb (
liczb (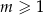 ), w tym
), w tym 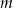 liczb 1 i
liczb 1 i 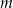 liczb 3. Odchylenie standardowe tego zestawu liczb jest równe
liczb 3. Odchylenie standardowe tego zestawu liczb jest równe
A) 1 B) 2 C) 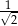 D)
D) 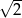
W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [19 dag, 21 dag]. Pobrano próbę kontrolną liczącą 50 jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie.
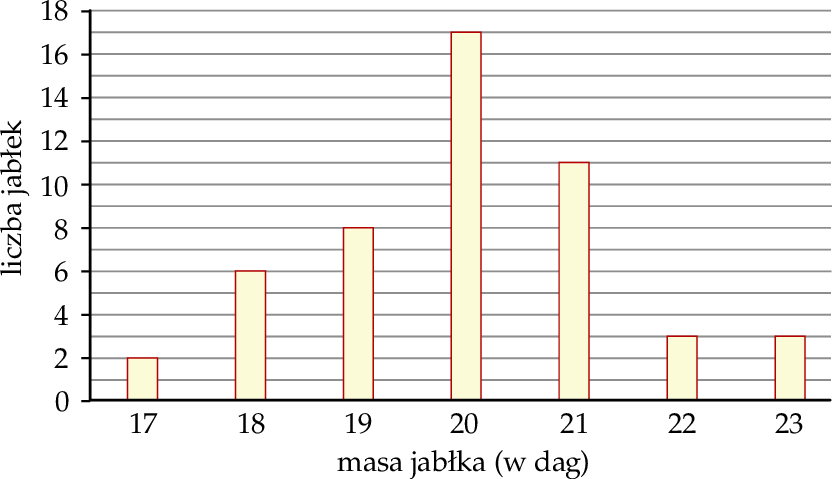
Średnia masy 50 zważonych jabłek z pobranej próby kontrolnej jest
| A) mniejsza niż 21 dag, | B) większa niż 21 dag, |
ponieważ
| 1) | większość jabłek waży 20 dag. |
| 2) | suma iloczynów masy i liczby jabłek o takiej masie jest mniejsza niż 1050 dag. |
| 3) | większość jabłek waży co najmniej 20 dag. |
Mediana danych 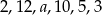 jest równa 7. Wówczas
jest równa 7. Wówczas
A) 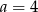 B)
B) 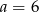 C)
C) 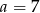 D)
D) 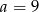
Mediana zestawu sześciu danych liczb: 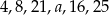 jest równa 14. Zatem
jest równa 14. Zatem
A) 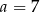 B)
B) 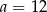 C)
C) 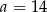 D)
D) 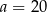
Medianą zestawu danych 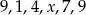 jest liczba 8. Wtedy
jest liczba 8. Wtedy  może być równe
może być równe
A) 8 B) 4 C) 7 D) 9
Medianą zestawu danych  jest liczba 4. Wtedy
jest liczba 4. Wtedy  może być równe
może być równe
A) 2 B) 3 C) 4 D) 5
Mediana zestawu ośmiu danych liczb: 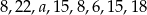 jest równa 14. Zatem
jest równa 14. Zatem
A) 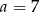 B)
B) 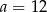 C)
C) 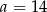 D)
D) 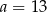
Mediana danych 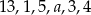 jest równa 4. Wówczas
jest równa 4. Wówczas
A) 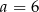 B)
B) 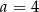 C)
C) 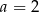 D)
D) 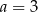
Mediana danych 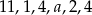 jest równa 3. Wówczas
jest równa 3. Wówczas
A) 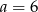 B)
B) 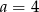 C)
C) 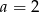 D)
D) 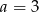
Średnia arytmetyczna zestawu pewnych stu liczb całkowitych dodatnich jest równa  . Każdą z liczb tego zestawu zwiększamy o 4, w wyniku czego otrzymujemy nowy zestaw stu liczb. Średnia arytmetyczna nowego zestawu stu liczb jest równa
. Każdą z liczb tego zestawu zwiększamy o 4, w wyniku czego otrzymujemy nowy zestaw stu liczb. Średnia arytmetyczna nowego zestawu stu liczb jest równa
A) 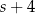 B)
B) 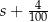 C)
C) 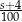 D)
D) 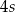
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
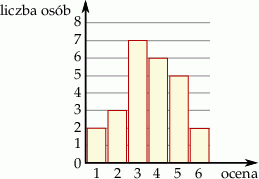
Średnia ocen ze sprawdzianu jest równa
A) 4 B) 3,6 C) 3,5 D) 3
Średnia arytmetyczna danych przedstawionych na diagramie częstości jest równa
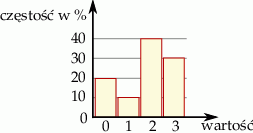
A) 1 B) 1,2 C) 1,5 D) 1,8
Średnia danych przestawionych na wykresie słupkowym jest równa:
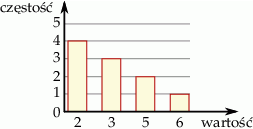
A) 8,25 B) 4 C) 3,3 D) 0,625
Średnia arytmetyczna danych przedstawionych na diagramie częstości jest równa
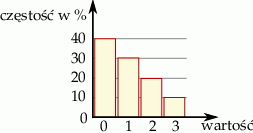
A) 1 B) 1,2 C) 1,5 D) 1,8
Na diagramie poniżej znajdują się wyniki z matematyki uczniów klasy IIIA na pierwszy semestr.
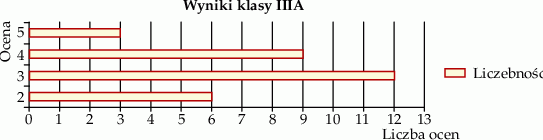
Średnia ocen z matematyki w tej klasie jest równa:
A) 3 B) 3,3 C) 3,5 D) 3,8
Na diagramie przedstawiono rozkład wynagrodzenia brutto wszystkich stu pracowników pewnej firmy za styczeń 2023 roku.
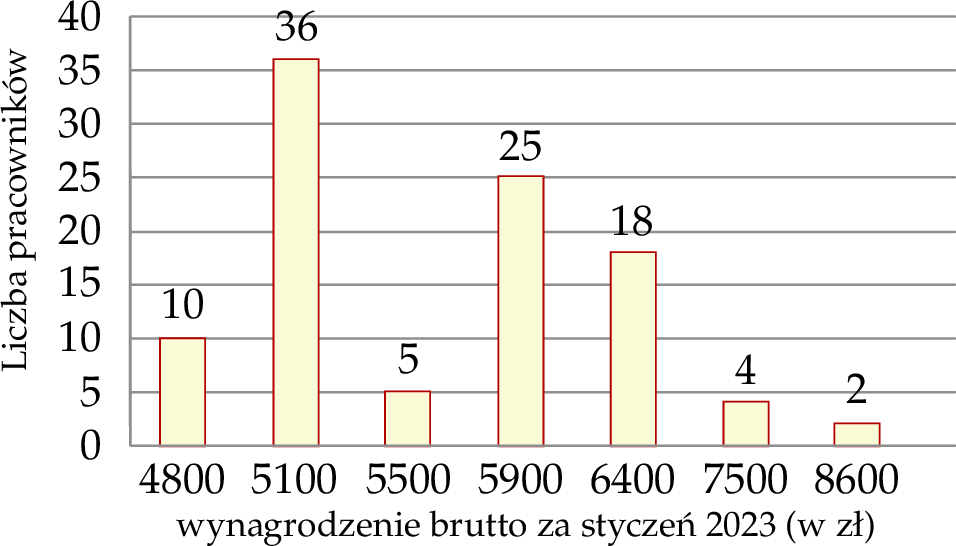
Średnia wynagrodzenia brutto wszystkich pracowników tej firmy za styczeń 2023 roku jest równa
A) 5 690 zł B) 5 280 zł C) 6 257 zł D) 5 900 zł
Na diagramie przedstawiono rozkład wynagrodzenia brutto wszystkich stu pracowników pewnej firmy za styczeń 2024 roku.
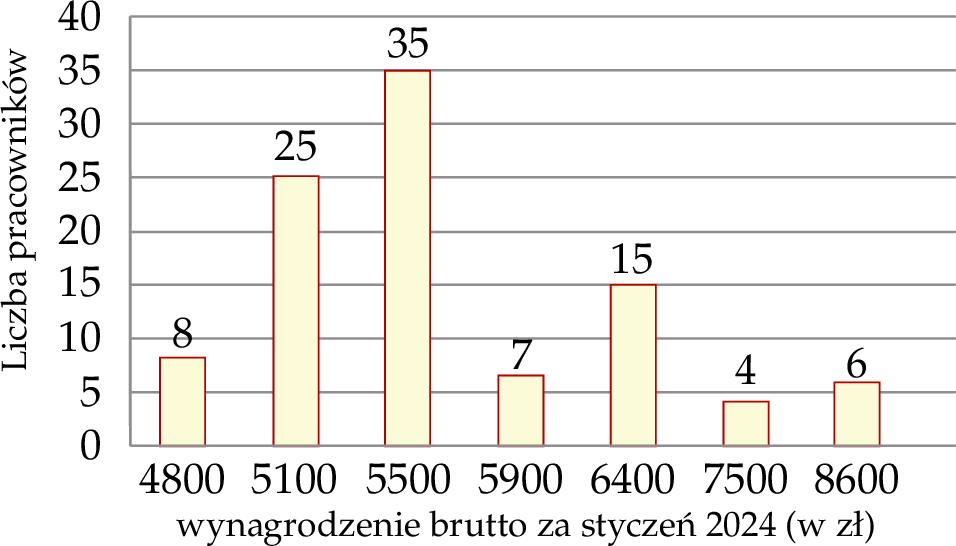
Średnia wynagrodzenia brutto wszystkich pracowników tej firmy za styczeń 2024 roku jest równa
A) 7 300 zł B) 5 280 zł C) 6 257 zł D) 5 773 zł
Firma  zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy
zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy  , którzy otrzymują płacę miesięczną w danej wysokości.
, którzy otrzymują płacę miesięczną w danej wysokości.
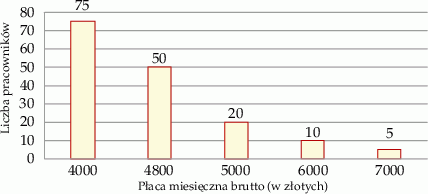
Średnia miesięczna płaca brutto w firmie  jest równa
jest równa
A) 4 593,75 zł B) 4 800,00 zł C) 5 360,00 zł D) 2 399,33 zł
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
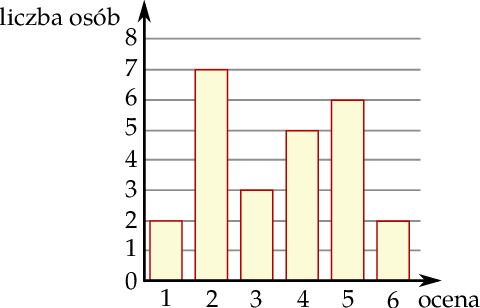
Średnia ocen ze sprawdzianu jest równa
A) 3,48 B) 4 C) 3,5 D) 3
Przeprowadzono badanie dotyczące liczby samochodów osobowych w rodzinie. Wyniki przedstawia poniższy diagram
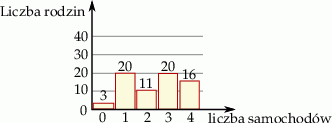
Wartość średnia liczby samochodów w rodzinie wynosi
A) 2 B) 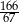 C)
C) 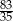 D) 3
D) 3
Na diagramie przedstawiono wyniki sprawdzianu z matematyki w pewnej klasie maturalnej. Na osi poziomej podano oceny, które uzyskali uczniowie tej klasy, a na osi pionowej podano liczbę uczniów, którzy otrzymali daną ocenę.
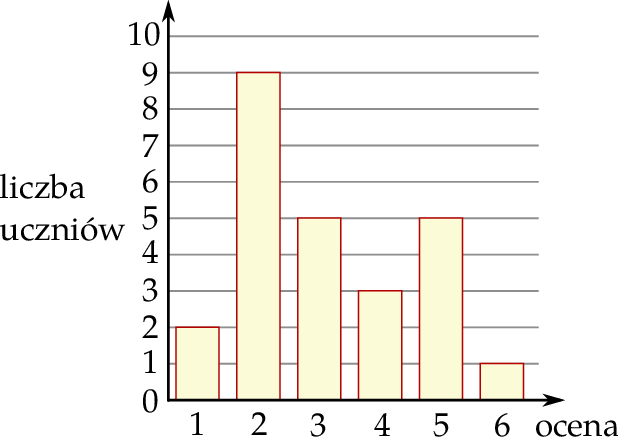
Średnia arytmetyczna ocen uzyskanych z tego sprawdzianu przez uczniów tej klasy jest równa
A) 3 B) 3,12 C) 3,5 D) 4,1(6)
Średnia arytmetyczna danych przedstawionych na diagramie częstości jest równa
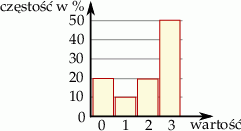
A) 2 B) 1 C) 1,5 D) 1,8
Firma  zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy
zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy  , którzy otrzymują płacę miesięczną w danej wysokości.
, którzy otrzymują płacę miesięczną w danej wysokości.
Średnia miesięczna płaca brutto w firmie 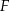 jest równa
jest równa
A) 4 862,5 zł B) 4 800,00 zł C) 5 360,00 zł D) 4 593,75 zł
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
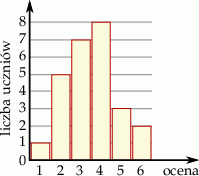
Średnia ocen uzyskanych przez uczniów z tego sprawdzianu jest równa
A) 2 B) 3 C) 3,5 D) 4
Sześć liczb: 19, 15, 13,  , 7, 1, tworzących zestaw danych, jest uporządkowanych malejąco. Mediana tego zestawu sześciu danych jest równa medianie zestawu pięciu danych: 15,
, 7, 1, tworzących zestaw danych, jest uporządkowanych malejąco. Mediana tego zestawu sześciu danych jest równa medianie zestawu pięciu danych: 15,  , 8, 2, 19. Zatem
, 8, 2, 19. Zatem
A) 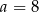 B)
B) 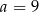 C)
C) 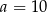 D)
D) 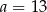
Janek w pierwszym semestrze otrzymał następujące oceny z matematyki: z prac klasowych 2, 3, 3, 4, z kartkówek 5, 5, 4, 4, 5, 5, z odpowiedzi ustnych 2, 3, 4. Oceny z prac klasowych mają wagę 0,5, z kartkówek 0,3, z odpowiedzi ustnych 0,2. Średnia ważona (zaokrąglona do dwóch miejsc po przecinku) ocen z matematyki Janka w pierwszym semestrze jest równa
A) 3,68 B) 3,58 C) 3,25 D) 1,23
Kasia w pierwszym semestrze otrzymała następujące oceny z matematyki: z prac klasowych 3, 4, 4, 2, z kartkówek 5, 4, 4, 3, 5, z zadań domowych 3, 4, 5. Oceny z prac klasowych mają wagę 5, z kartkówek 3, z zadania domowego 2. Średnia ważona (zaokrąglona do dwóch miejsc po przecinku) ocen z matematyki Kasi w pierwszym semestrze jest równa
A) 3,71 B) 4,6 C) 13,7 D) 11,41
Firma  zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy
zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy  , którzy otrzymują płacę miesięczną w danej wysokości.
, którzy otrzymują płacę miesięczną w danej wysokości.
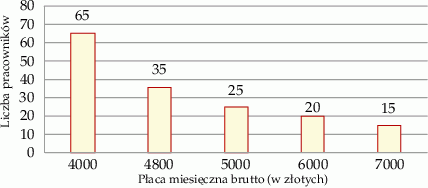
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Mediana miesięcznej płacy pracowników firmy 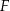 jest równa 4800 zł. jest równa 4800 zł. | P | F |
| Ponad 78% pracowników tej firmy zarabia nie więcej niż 5000 zł brutto. | P | F |
Średnia arytmetyczna zestawu danych: 3, 8, 3, 11, 3, 10, 3,  jest równa 6. Mediana tego zestawu jest równa
jest równa 6. Mediana tego zestawu jest równa
A) 5 B) 6 C) 7 D) 8
Średnia arytmetyczna zestawu danych:  , 2, 4, 6, 8, 10, 13, 16 jest równa 8,5. Wtedy mediana tego zestawu danych jest równa
, 2, 4, 6, 8, 10, 13, 16 jest równa 8,5. Wtedy mediana tego zestawu danych jest równa
A) 8 B) 8,5 C) 9 D) 10
Średnia arytmetyczna liczb: 3, 1, 6, 5, 2, 4,  , 2, 3, 8 wynosi 4. Medianą tego zbioru liczb jest
, 2, 3, 8 wynosi 4. Medianą tego zbioru liczb jest
A) 3,5 B) 3 C) 4,5 D) 4
Średnia arytmetyczna zestawu danych:  , 2, 4, 6, 8, 10, 12, 14 jest równa 9. Wtedy mediana tego zestawu danych jest równa
, 2, 4, 6, 8, 10, 12, 14 jest równa 9. Wtedy mediana tego zestawu danych jest równa
A) 8 B) 9 C) 10 D) 16
Średnia arytmetyczna zestawu danych: 4, 5, 3, 8, 10, 4, 8, 9, 6,  jest równa 6,5. Mediana tego zestawu jest równa
jest równa 6,5. Mediana tego zestawu jest równa
A) 5 B) 6 C) 7 D) 8
Średnia arytmetyczna liczb:  , 13, 7, 5, 5, 3, 2, 11 jest równa 7. Mediana tego zestawu liczb jest równa
, 13, 7, 5, 5, 3, 2, 11 jest równa 7. Mediana tego zestawu liczb jest równa
A) 6 B) 7 C) 10 D) 5
Średnia arytmetyczna sześciu liczb naturalnych: 31, 16, 25, 29, 27,  , jest równa
, jest równa 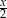 . Mediana tych liczb jest równa
. Mediana tych liczb jest równa
A) 26 B) 27 C) 28 D) 29
Średnia arytmetyczna sześciu liczb naturalnych: 21, 14, 19, 15, 24,  , jest równa
, jest równa 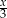 . Mediana tych liczb jest równa
. Mediana tych liczb jest równa
A) 17 B) 20 C) 19 D) 21
Mediana danych zawartych w tabeli liczebności jest równa 3.
| Wartość | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczebność | 3 | 4 |  | 1 | 2 | 6 |
Zatem  może być równe
może być równe
A) 0 B) 1 C) 2 D) 3
W tabeli poniżej przedstawione są wyniki pracy klasowej w dwóch klasach pierwszych.
| Ocena | 3,25 | 2,75 | 4,25 | 4 | 2 | 5,25 | 3,75 | 4,75 | 1 | 3 | 5 | 2,25 | 6 | 5,75 |
| Liczba ocen | 2 | 5 | 2 | 1 | 5 | 1 | 3 | 2 | 1 | 4 | 3 | 1 | 2 | 3 |
Mediana ocen w tych dwóch klasach jest równa
A) 4 B) 3 C) 3,25 D) 3,75
Średnia arytmetyczna pięciu liczb: 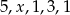 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 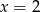 B)
B) 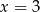 C)
C) 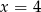 D)
D) 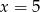
Średnia arytmetyczna siedmiu liczb: 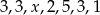 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 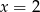 B)
B) 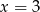 C)
C) 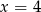 D)
D) 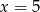
Dla jakiej wartości liczbowej  średnia arytmetyczna liczb:
średnia arytmetyczna liczb: 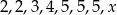 jest równa 4?
jest równa 4?
A) 6 B) 5 C) 4 D) 3
Średnia arytmetyczna sześciu liczb: 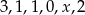 jest równa 2. Wtedy liczba
jest równa 2. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Średnia arytmetyczna pięciu liczb: 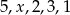 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 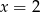 B)
B) 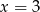 C)
C) 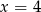 D)
D) 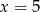
Średnia arytmetyczna ośmiu liczb: 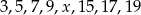 jest równa 11. Wtedy
jest równa 11. Wtedy
A) 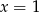 B)
B) 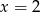 C)
C) 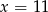 D)
D) 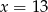
Średnia arytmetyczna zestawu danych: 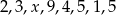 wynosi 4,5. Wynika z tego, że:
wynosi 4,5. Wynika z tego, że:
A) 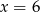 B)
B) 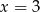 C)
C) 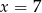 D)
D) 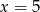
Średnia arytmetyczna pięciu liczb: 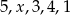 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 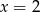 B)
B) 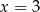 C)
C) 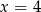 D)
D) 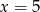
Średnia arytmetyczna zestawu sześciu liczb: 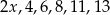 , jest równa 5. Wynika stąd, że
, jest równa 5. Wynika stąd, że
A) 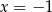 B)
B) 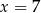 C)
C) 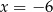 D)
D) 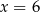
Średnia arytmetyczna dziesięciu liczb 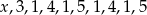 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 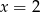 B)
B) 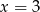 C)
C) 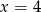 D)
D) 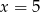
Średnia arytmetyczna zestawu danych: 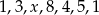 wynosi 4. Wynika z tego, że:
wynosi 4. Wynika z tego, że:
A) 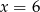 B)
B) 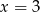 C)
C) 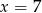 D)
D) 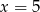
Średnia arytmetyczna liczb 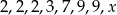 jest równa 4,5. Liczba
jest równa 4,5. Liczba  jest równa
jest równa
A) 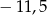 B) 1 C) 1,5 D) 2
B) 1 C) 1,5 D) 2
Średnia arytmetyczna dziesięciu liczb 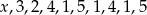 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 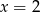 B)
B) 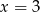 C)
C) 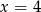 D)
D) 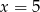
Średnia arytmetyczna liczb: 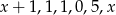 jest równa
jest równa  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A)  B) 2 C)
B) 2 C)  D)
D) 
Średnia arytmetyczna zestawu danych: 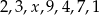 wynosi
wynosi 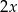 . Wynika z tego, że:
. Wynika z tego, że:
A) 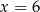 B)
B) 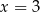 C)
C) 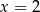 D)
D) 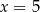
Średnia arytmetyczna pięciu liczb: 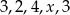 jest równa 3,2. Wtedy
jest równa 3,2. Wtedy
A) 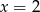 B)
B) 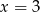 C)
C) 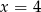 D)
D) 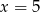
Średnia arytmetyczna ocen Jacka jest równa 3,75, a średnia ocen Karola (liczona z dokładnie tej samej liczby ocen) jest równa 4,25. Średnia ocen obu chłopców jest równa
A) 3,95 B) 4,5 C) 4,0 D) 4,15
Średnia arytmetyczna ocen Zosi jest równa 2,8, a średnia ocen Basi (liczona z dokładnie tej samej liczby ocen) jest równa 4,4. Średnia ocen obu dziewcząt jest równa
A) 3,6 B) 4,0 C) 3,8 D) 4,15

