Nieskończony ciąg geometryczny 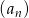 jest określony wzorem
jest określony wzorem 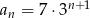 , dla
, dla 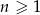 . Oblicz iloraz
. Oblicz iloraz 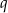 tego ciągu.
tego ciągu.
/Szkoła średnia
Nieskończony ciąg geometryczny 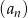 jest określony wzorem
jest określony wzorem 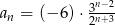 , dla
, dla 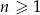 . Oblicz iloraz
. Oblicz iloraz 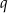 tego ciągu.
tego ciągu.
Nieskończony ciąg geometryczny 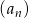 jest określony wzorem
jest określony wzorem 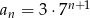 , dla
, dla 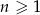 . Oblicz iloraz
. Oblicz iloraz 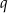 tego ciągu.
tego ciągu.
Punkt 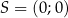 jest środkiem boku
jest środkiem boku 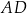 równoległoboku
równoległoboku 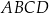 . Wiadomo też, że
. Wiadomo też, że ![−→ AB = [4;3]](https://img.zadania.info/zad/9290117/HzadT3x.png) oraz
oraz ![−→ BC = [6;2]](https://img.zadania.info/zad/9290117/HzadT4x.png) . Wyznacz wierzchołki tego równoległoboku.
. Wyznacz wierzchołki tego równoległoboku.
Ostrosłupy prawidłowe trójkątne 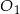 i
i 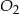 mają takie same wysokości. Długość krawędzi podstawy ostrosłupa
mają takie same wysokości. Długość krawędzi podstawy ostrosłupa 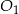 jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa
jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa 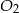 . Stosunek objętości ostrosłupa
. Stosunek objętości ostrosłupa 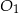 do objętości ostrosłupa
do objętości ostrosłupa 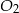 jest równy
jest równy
A) 3 : 1 B) 1 : 3 C) 9 : 1 D) 1 : 9
Na bokach trójkąta prostokątnego zbudowano trójkąty równoboczne, których pola są odpowiednio równe 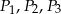 . Wówczas
. Wówczas
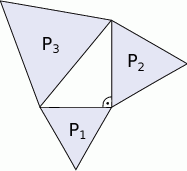
A) 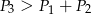 B)
B) 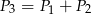 C)
C) 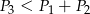 D)
D) 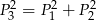
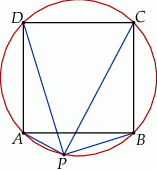
Punkt 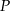 należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 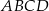 . Wykaż, że
. Wykaż, że 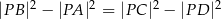 .
.
Wykaż, że prosta 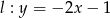 jest styczna do okręgu
jest styczna do okręgu 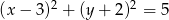 .
.
Sprawdź, czy prosta 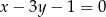 jest styczna do okręgu
jest styczna do okręgu 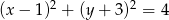 .
.
Dany jest ostrosłup prawidłowy czworokątny 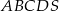 o podstawie
o podstawie 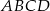 . W trójkącie równoramiennym
. W trójkącie równoramiennym 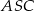 stosunek długości podstawy do długości ramienia jest równy
stosunek długości podstawy do długości ramienia jest równy 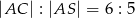 . Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
Narysuj linię o równaniu 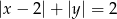 i oblicz jej długość.
i oblicz jej długość.
W trójkącie 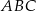 długości boków
długości boków 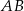 i
i 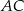 są odpowiednio równe 4 i 6, a długość środkowej
są odpowiednio równe 4 i 6, a długość środkowej 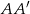 jest równa
jest równa 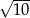 . Oblicz długość boku
. Oblicz długość boku 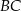 .
.
Rozwiąż równanie 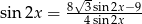 , gdzie
, gdzie 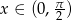 .
.
Kąt  jest ostry oraz
jest ostry oraz 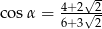 . Wtedy
. Wtedy 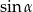 jest równy
jest równy
A) 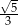 B)
B) 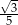 C)
C) 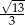 D)
D) 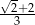
Wielomian 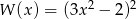 jest równy wielomianowi
jest równy wielomianowi
A) 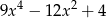 B)
B) 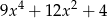 C)
C) 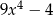 D)
D) 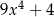
Wielomian 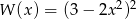 jest równy wielomianowi
jest równy wielomianowi
A) 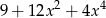 B)
B) 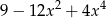 C)
C) 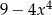 D)
D) 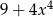
Równanie 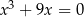
A) nie ma pierwiastków B) ma jeden pierwiastek
C) ma dwa pierwiastki D) ma trzy pierwiastki
Równanie 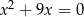
A) nie ma pierwiastków B) ma jeden pierwiastek
C) ma dwa pierwiastki D) ma trzy pierwiastki
Równanie 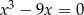
A) nie ma pierwiastków B) ma jeden pierwiastek
C) ma dwa pierwiastki D) ma trzy pierwiastki
Suma długości przyprostokątnych trójkąta prostokątnego jest równa 7. Jaka jest najmniejsza możliwa długość przeciwprostokątnej tego trójkąta?
Ciąg 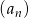 jest określony wzorem
jest określony wzorem 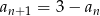 dla każdej liczby naturalnej
dla każdej liczby naturalnej 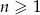 . Suma pięćdziesięciu początkowych wyrazów tego ciągu jest równa
. Suma pięćdziesięciu początkowych wyrazów tego ciągu jest równa
A) 150 B) 75 C) 50 D) 100
Oblicz pole trójkąta równoramiennego 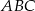 , w którym
, w którym 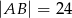 i
i 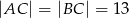 .
.
Dla jakich wartości parametru 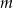 pierwiastkami równania
pierwiastkami równania 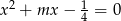 są liczby liczby
są liczby liczby 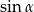 i
i 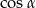 dla pewnego
dla pewnego 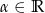 ?
?
Prostokąt 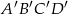 jest podobny do prostokąta
jest podobny do prostokąta 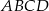 w skali
w skali 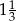 . Pole prostokąta
. Pole prostokąta 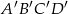 jest równe
jest równe 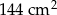 . Krótszy bok prostokąta
. Krótszy bok prostokąta 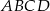 ma długość 6 cm. Oblicz długości pozostałych boków tych prostokątów.
ma długość 6 cm. Oblicz długości pozostałych boków tych prostokątów.
Prostokąt 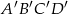 jest podobny do prostokąta
jest podobny do prostokąta 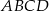 w skali
w skali 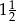 . Pole prostokąta
. Pole prostokąta 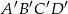 jest równe
jest równe 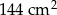 . Krótszy bok prostokąta
. Krótszy bok prostokąta 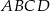 ma długość 9 cm. Oblicz długości pozostałych boków tych prostokątów.
ma długość 9 cm. Oblicz długości pozostałych boków tych prostokątów.
Iloczyn cyfr liczby dwucyfrowej jest o 11 większy od sumy jej cyfr. Jeżeli przestawimy cyfry w tej liczbie, to otrzymamy liczbę o 36 większą od początkowej. Wyznacz tę liczbę.
Wiadomo, że tangens kąta ostrego  jest równy
jest równy  . Wobec tego:
. Wobec tego:
A) 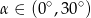 B)
B) 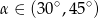 C)
C) 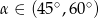 D)
D) 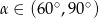
Wiadomo, że tangens kąta ostrego  jest równy
jest równy  . Wobec tego:
. Wobec tego:
A) 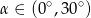 B)
B) 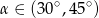 C)
C) 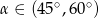 D)
D) 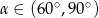
Wiadomo, że tangens kąta ostrego  jest równy
jest równy 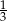 . Wobec tego:
. Wobec tego:
A) 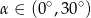 B)
B) 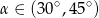 C)
C) 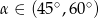 D)
D)