Podstawy trapezu równoramiennego o polu 40 mają długości 6 i 14. Oblicz długość ramienia tego trapezu.
/Szkoła średnia
Punkty 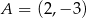 i
i 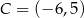 są wierzchołkami rombu
są wierzchołkami rombu 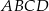 . Środkiem okręgu wpisanego w romb jest punkt
. Środkiem okręgu wpisanego w romb jest punkt
A) 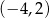 B)
B) 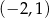 C)
C) 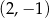 D)
D) 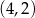
Punkty 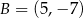 i
i 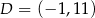 są wierzchołkami rombu
są wierzchołkami rombu 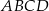 . Środkiem okręgu wpisanego w romb jest punkt
. Środkiem okręgu wpisanego w romb jest punkt
A) 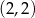 B)
B) 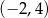 C)
C) 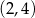 D)
D) 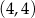
Stosunek długości przekątnych rombu o boku 17 cm jest równy 5:3. Oblicz pole rombu.
Stosunek długości przekątnych rombu o boku 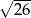 jest równy 3:2. Oblicz pole tego rombu.
jest równy 3:2. Oblicz pole tego rombu.
Punkt 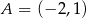 jest wierzchołkiem rombu o polu równym 20. Punkt
jest wierzchołkiem rombu o polu równym 20. Punkt 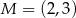 jest środkiem symetrii tego rombu. Wyznacz równanie okręgu wpisanego w ten romb.
jest środkiem symetrii tego rombu. Wyznacz równanie okręgu wpisanego w ten romb.
W równoległoboku 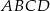 , w którym
, w którym 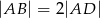 punkt
punkt 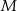 jest środkiem boku
jest środkiem boku 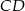 . Wykaż, że trójkąt
. Wykaż, że trójkąt 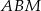 jest prostokątny.
jest prostokątny.
Punkty 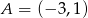 i
i 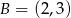 są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
A) 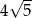 B)
B) 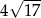 C)
C) 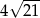 D)
D) 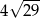
Punkty 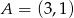 i
i 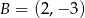 są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
A) 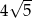 B)
B) 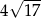 C)
C) 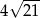 D)
D) 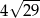
Wiedząc, że liczba 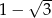 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 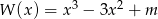 , wyznacz wartość parametru
, wyznacz wartość parametru 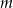 .
.
Wyznacz wszystkie rozwiązania równania 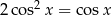 należące do przedziału
należące do przedziału 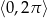 .
.
Rozwiąż równanie 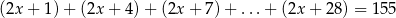 , jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
, jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
Rozwiąż równanie 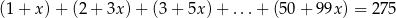 , jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
, jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
Rozwiąż równanie 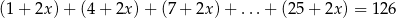 , jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
, jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
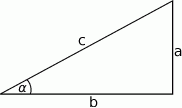
W trójkącie prostokątnym na rysunku 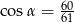 . Wiedząc, że dłuższa przyprostokątna jest o 2 cm krótsza od przeciwprostokątnej, wyznacz długości boków
. Wiedząc, że dłuższa przyprostokątna jest o 2 cm krótsza od przeciwprostokątnej, wyznacz długości boków 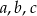 .
.
Pewnego dnia w klasie liczącej 11 dziewcząt i 15 chłopców nieobecny był jeden chłopiec i jedna dziewczynka. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 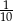 B)
B) 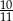 C)
C) 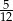 D)
D) 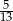
Pewnego dnia w klasie liczącej 16 dziewcząt i 12 chłopców nieobecnych było dwóch chłopców i trzy dziewczynki. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 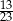 B)
B) 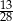 C)
C) 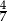 D)
D) 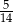
Wykaż, że dla dowolnych liczb rzeczywistych 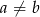 oraz
oraz 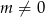 równanie
równanie
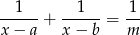
ma dwa różne rozwiązania.
Dane są dwa okręgi o promieniach 12 i 17. Mniejszy okrąg przechodzi przez środek większego okręgu. Odległość między środkami tych okręgów jest równa
A) 5 B) 12 C) 17 D) 29
Dane są dwa okręgi o promieniach 10 i 15. Mniejszy okrąg przechodzi przez środek większego okręgu. Odległość między środkami tych okręgów jest równa
A) 2,5 B) 5 C) 10 D) 12,5
Dane są dwa okręgi o promieniach 10 i 18. Większy okrąg przechodzi przez środek mniejszego okręgu. Odległość między środkami tych okręgów jest równa
A) 18 B) 8 C) 10 D) 28
Dane są dwa okręgi o promieniach 12 i 17. Większy okrąg przechodzi przez środek mniejszego okręgu. Odległość między środkami tych okręgów jest równa
A) 5 B) 12 C) 17 D) 29
Wyznacz najmniejszą i największą wartość funkcji 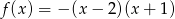 w przedziale
w przedziale 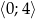 .
.
Oblicz najmniejszą i największą wartość funkcji kwadratowej 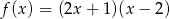 w przedziale
w przedziale 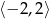 .
.
Wyznacz najmniejszą i największą wartość funkcji 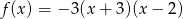 w przedziale
w przedziale 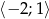 .
.
Wyznacz najmniejszą i największą wartość funkcji 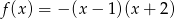 w przedziale
w przedziale 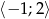 .
.
Oblicz prawdopodobieństwo, że w czterech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 5.
Wyznacz zbiór wartości funkcji
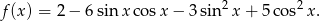
Mariusz Czerkawski i Jimmy O’Brien w jednym sezonie NHL zdobyli w sumie 100 bramek. Kluby obu zawodników za każdą zdobytą bramkę wypłacały hokeistom z góry ustaloną premię. Po sezonie okazało się, że obaj zawodnicy otrzymali za strzelone bramki równe kwoty. Gdyby Czerkawski zdobył tyle bramek ile O’Brien, to otrzymałby 72000$, zaś gdyby drugi strzelił tyle bramek ile pierwszy, to otrzymałby 32000$. Oblicz, ile bramek zdobył każdy z nich i jaka była wysokość premii w obu klubach za strzelenie bramki.
W trójkącie 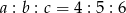 . Wykaż, że w tym trójkącie
. Wykaż, że w tym trójkącie 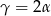 .
.
Wierzchołki kwadratu 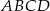 połączono ze środkami jego boków (zobacz rysunek) i otrzymano w ten sposób mniejszy kwadrat
połączono ze środkami jego boków (zobacz rysunek) i otrzymano w ten sposób mniejszy kwadrat 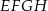 . Oblicz, jaki jest stosunek obwodów kwadratów
. Oblicz, jaki jest stosunek obwodów kwadratów 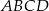 i
i 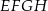 .
.
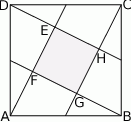
Wskaż liczbę, której 4% jest równe 8.
A) 3,2 B) 32 C) 100 D) 200
Jeżeli 8,5% liczby  jest równe 163,2, to liczba
jest równe 163,2, to liczba  jest równa
jest równa
A) 19200 B) 1920 C) 1387,2 D) 13872
4,5% liczby  jest równe 48,6. Liczba
jest równe 48,6. Liczba  jest równa
jest równa
A) 1080 B) 108 C) 48,6 D) 4,86
Wskaż liczbę, której 0,4% jest równe 12.
A) 0,048 B) 0,48 C) 30 D) 3000
Liczba 42 jest równa 0,6% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 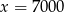 B)
B) 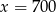 C)
C) 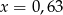 D)
D) 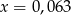
Jeżeli 35% pewnej liczby  jest równe 140 to
jest równe 140 to
A) 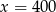 B)
B) 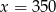 C)
C) 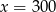 D)
D) 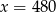
Liczba 78 stanowi 150% liczby  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 60 B) 52 C) 48 D) 39
Liczba 609 stanowi 140% liczby  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 420 B) 435 C) 468 D) 406
Wskaż liczbę, której 6% jest równe 6.
A) 0,36 B) 3,6 C) 10 D) 100

