Wyrażenie 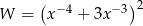 jest równe
jest równe
A) 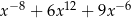 B)
B) 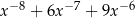
C) 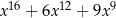 D)
D) 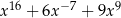
/Szkoła średnia
Wyrażenie 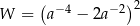 jest równe
jest równe
A) 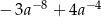 B)
B) 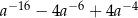
C) 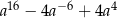 D)
D) 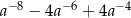
Wyrażenie 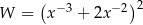 jest równe
jest równe
A) 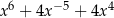 B)
B) 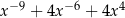
C) 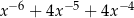 D)
D) 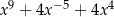
Kąt rozwarcia stożka ma miarę 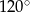 , a jego tworząca ma długość 10. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
, a jego tworząca ma długość 10. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
A) 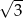 B)
B) 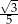 C) 5 D)
C) 5 D) 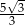
Kąt rozwarcia stożka ma miarę 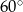 , a jego tworząca ma długość 8. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
, a jego tworząca ma długość 8. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
A) 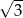 B)
B) 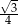 C)
C) 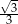 D)
D) 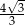
Kąt rozwarcia stożka ma miarę 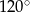 , a jego tworząca ma długość 12. Wówczas stosunek wysokości stożka do jego promienia podstawy jest równy
, a jego tworząca ma długość 12. Wówczas stosunek wysokości stożka do jego promienia podstawy jest równy
A) 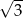 B)
B) 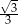 C)
C) 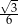 D)
D) 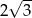
Wskaż największą liczbę całkowitą spełniającą nierówność 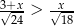 .
.
A) 9 B) 17 C) 13 D) 19
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 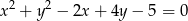 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 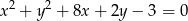 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 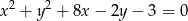 .
.
Kąt  jest ostry i spełniona jest równość
jest ostry i spełniona jest równość  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 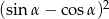 .
.
Dany jest kąt  , dla którego spełniona jest równość
, dla którego spełniona jest równość 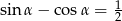 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 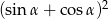 .
.
Na boku 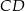 prostokąta
prostokąta 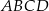 wybrano punkt
wybrano punkt 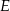 taki, że
taki, że 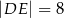 . Przekątna
. Przekątna 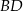 i odcinek
i odcinek 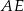 przecinają się w punkcie
przecinają się w punkcie 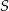 oraz
oraz 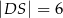 . Bok
. Bok 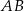 prostokąta
prostokąta 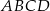 ma długość 12 (zobacz rysunek).
ma długość 12 (zobacz rysunek).
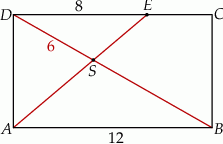
Oblicz długość odcinka 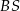 .
.
W graniastosłupie prawidłowym sześciokątnym 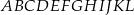 wierzchołki
wierzchołki 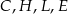 połączono odcinkami (tak jak na rysunku).
połączono odcinkami (tak jak na rysunku).
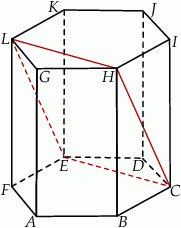
Wskaż kąt między bokiem 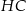 czworokąta
czworokąta 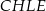 i płaszczyzną podstawy tego graniastosłupa.
i płaszczyzną podstawy tego graniastosłupa.
A) 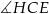 B)
B) 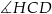 C)
C) 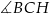 D)
D) 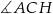
Granica ciągu 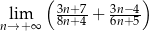 jest równa
jest równa
A) 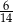 B)
B)  C)
C) 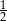 D)
D) 
Granica ciągu 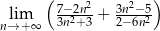 jest równa
jest równa
A) 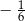 B)
B)  C)
C) 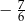 D)
D) 
Iloraz nieskończonego ciągu geometrycznego 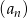 jest równy
jest równy 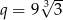 . Wynika stąd, że
. Wynika stąd, że
A) 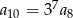 B)
B) 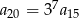 C)
C) 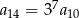 D)
D) 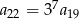
Rozwiąż równanie 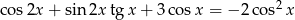 w przedziale
w przedziale 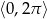 .
.
Najmniejszą liczbą całkowitą spełniającą nierówność 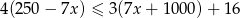 jest
jest
A) 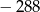 B)
B) 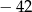 C)
C) 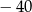 D)
D) 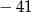
Najmniejszą liczbą całkowitą spełniającą nierówność 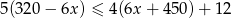 jest
jest
A) 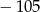 B)
B) 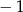 C)
C) 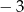 D)
D) 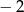
Punkty 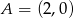 i
i 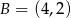 leżą na okręgu o równaniu
leżą na okręgu o równaniu 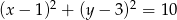 . Wyznacz na tym okręgu taki punkt
. Wyznacz na tym okręgu taki punkt 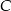 , aby trójkąt
, aby trójkąt 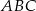 był trójkątem równoramiennym o podstawie
był trójkątem równoramiennym o podstawie 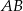 .
.
Równanie 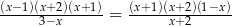
A) ma cztery różne rozwiązania: 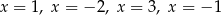 .
.
B) ma trzy różne rozwiązania: 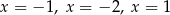 .
.
C) ma dwa różne rozwiązania: 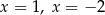 .
.
D) ma dwa różne rozwiązania: 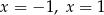 .
.
Punkty 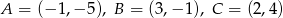 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 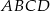 . Oblicz pole tego równoległoboku.
. Oblicz pole tego równoległoboku.
Oblicz pole równoległoboku 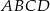 o wierzchołkach
o wierzchołkach 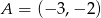 ,
, 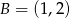 ,
, 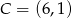 ,
, 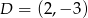 .
.
Wierzchołek paraboli będącej wykresem funkcji 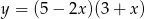 ma współrzędne
ma współrzędne
A) 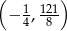 B)
B) 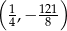 C)
C) 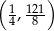 D)
D) 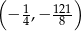
Wierzchołek paraboli będącej wykresem funkcji 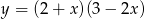 ma współrzędne
ma współrzędne
A) 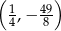 B)
B) 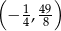 C)
C) 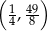 D)
D) 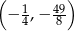
Wykaż, że jeżeli liczby rzeczywiste 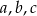 spełniają warunek
spełniają warunek 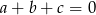 , to
, to
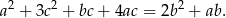
Do wykresu funkcji liniowej 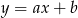 należą punkty
należą punkty 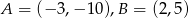 . Wynika stąd, że
. Wynika stąd, że
A) 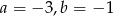 B)
B) 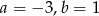 C)
C) 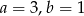 D)
D) 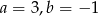
Jeżeli wiadomo, że punkty 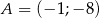 i
i 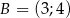 należą do wykresu funkcji liniowej, to ta funkcja opisana jest wzorem
należą do wykresu funkcji liniowej, to ta funkcja opisana jest wzorem
A) 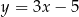 B)
B) 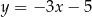 C)
C) 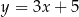 D)
D) 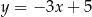
Do wykresu funkcji liniowej 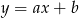 należą punkty
należą punkty 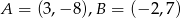 . Wynika stąd, że
. Wynika stąd, że
A) 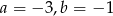 B)
B) 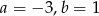 C)
C) 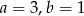 D)
D) 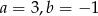
Do wykresu funkcji liniowej 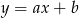 należą punkty
należą punkty 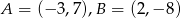 . Wynika stąd, że
. Wynika stąd, że
A) 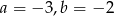 B)
B) 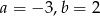 C)
C) 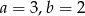 D)
D) 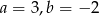
Do wykresu funkcji liniowej należą punkty 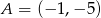 ,
, 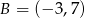 , zatem funkcja liniowa ma wzór
, zatem funkcja liniowa ma wzór
A) 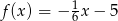 B)
B) 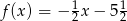 C)
C) 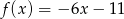 D)
D) 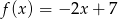
Promień okręgu opisanego na podstawie graniastosłupa prawidłowego trójkątnego ma długość 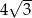 . Pole powierzchni bocznej jest równe 144.
. Pole powierzchni bocznej jest równe 144.
- Oblicz objętość tego graniastosłupa.
- Oblicz cosinus kąta między przekątną ściany bocznej i krawędzią podstawy graniastosłupa.
Dane są punkty 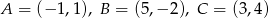 .
.
- Wyznacz równanie prostej przechodzącej przez punkt
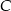 i prostopadłej do prostej
i prostopadłej do prostej 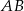 .
. - Oblicz pole trójkąta
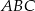 .
.
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 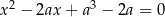 dwa różne rozwiązania dodatnie.
dwa różne rozwiązania dodatnie.

