Wyrażenie 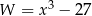 jest równe
jest równe
A) 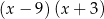 B)
B) 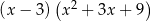
C) 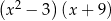 D)
D) 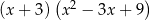
/Szkoła średnia
Wyrażenie 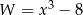 jest równe
jest równe
A) 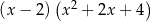 B)
B) 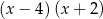
C) 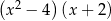 D)
D) 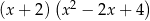
Wyrażenie 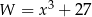 jest równe
jest równe
A) 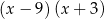 B)
B) 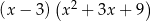
C) 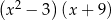 D)
D) 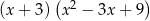
Wyprowadź wzór 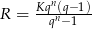 na wysokość raty
na wysokość raty 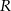 kredytu udzielonego w kwocie
kredytu udzielonego w kwocie 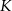 , przy założeniu, że:
, przy założeniu, że:
– spłata tego kredytu jest rozłożona na  równych rat płaconych miesięcznie;
równych rat płaconych miesięcznie;
– pierwszą ratę wpłacamy po miesiącu od daty udzielenia kredytu;
– roczne oprocentowanie kredytu jest równe  i
i 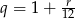 .
.
Dla jakich wartości parametru 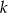 rozwiązanie układu równań
rozwiązanie układu równań 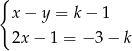 spełnia warunek
spełnia warunek 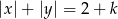 ?
?
Suma  początkowych wyrazów ciągu geometrycznego
początkowych wyrazów ciągu geometrycznego 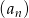 wyraża się wzorem
wyraża się wzorem 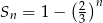 dla
dla 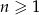 . Oblicz pierwszy wyraz ciągu i jego iloraz.
. Oblicz pierwszy wyraz ciągu i jego iloraz.
Prosta równoległa do jednego boku trójkąta dzieli jego pole na połowy. W jakim stosunku prosta ta dzieli pozostałe boki trójkąta?
Wykaż, że jeżeli 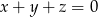 to zachodzi równość
to zachodzi równość
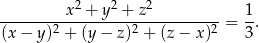
Wykaż, że jeśli 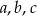 są dowolnymi liczbami rzeczywistymi takimi, że
są dowolnymi liczbami rzeczywistymi takimi, że 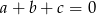 , to
, to
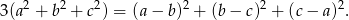
Wartość wyrażenia 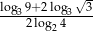 jest równa
jest równa
A)  B)
B)  C) 4 D) 9
C) 4 D) 9
W układzie współrzędnych punkty 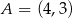 i
i 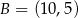 są wierzchołkami trójkąta
są wierzchołkami trójkąta 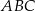 . Wierzchołek
. Wierzchołek 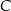 leży na prostej o równaniu
leży na prostej o równaniu 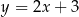 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 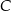 , dla którego kąt
, dla którego kąt 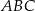 jest prosty.
jest prosty.
W układzie współrzędnych punkty 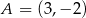 i
i 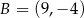 są wierzchołkami trójkąta
są wierzchołkami trójkąta 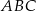 . Wierzchołek
. Wierzchołek 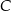 leży na prostej o równaniu
leży na prostej o równaniu 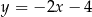 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 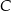 , dla którego kąt
, dla którego kąt 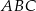 jest prosty.
jest prosty.
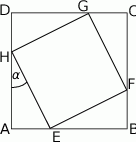
W kwadrat 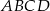 o boku długości 17 wpisano kwadrat
o boku długości 17 wpisano kwadrat 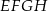 , jak pokazano na rysunku. Wiedząc, że przekątna kwadratu
, jak pokazano na rysunku. Wiedząc, że przekątna kwadratu 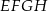 ma długość
ma długość 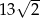 oblicz tangens kąta
oblicz tangens kąta  zaznaczonego na rysunku.
zaznaczonego na rysunku.
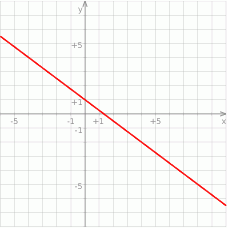
Na rysunku przedstawiony jest wykres funkcji liniowej  .
.
Funkcja 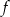 jest określona wzorem
jest określona wzorem
A) 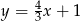 B)
B) 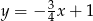 C)
C) 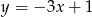 D)
D) 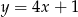
Na rysunku przedstawiony jest wykres funkcji liniowej 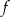 .
.
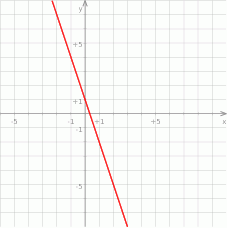
Funkcja 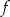 jest określona wzorem
jest określona wzorem
A) 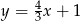 B)
B) 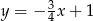 C)
C) 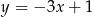 D)
D) 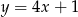
Na rysunku przedstawiony jest wykres funkcji liniowej 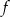 .
.
Funkcja  jest określona wzorem
jest określona wzorem
A) 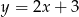 B)
B) 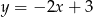 C)
C) 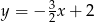 D)
D) 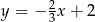
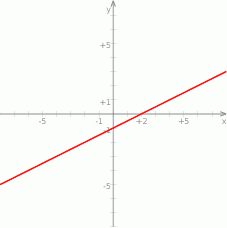
Wskaż wzór funkcji, której wykres przedstawiono na poniższym rysunku.
A) 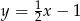 B)
B) 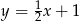 C)
C) 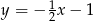 D)
D) 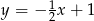
Wskaż wzór funkcji, której wykres przedstawiono na poniższym rysunku.
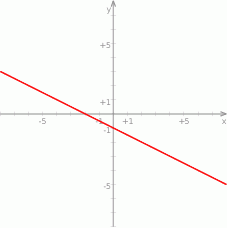
A) 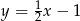 B)
B) 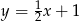 C)
C) 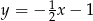 D)
D) 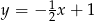
Na rysunku przedstawiony jest wykres funkcji liniowej 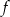 .
.
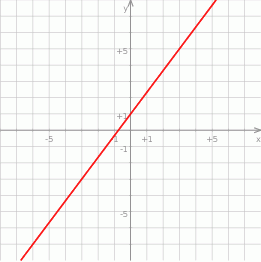
Funkcja 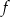 jest określona wzorem
jest określona wzorem
A) 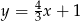 B)
B) 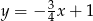 C)
C) 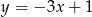 D)
D) 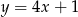
Na rysunku przedstawiony jest wykres funkcji liniowej 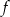 .
.
Funkcja  jest określona wzorem
jest określona wzorem
A) 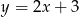 B)
B) 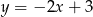 C)
C) 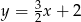 D)
D) 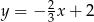
Na rysunku przedstawiony jest wykres funkcji liniowej 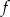 .
.
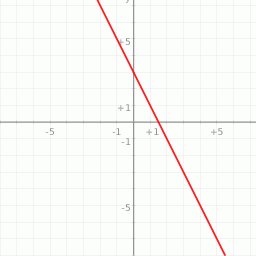
Funkcja 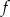 jest określona wzorem
jest określona wzorem
A) 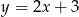 B)
B) 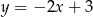 C)
C) 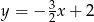 D)
D) 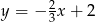
Na rysunku przedstawiono wykres funkcji 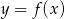 .
.
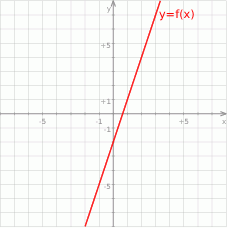
Wzór opisujący funkcję 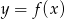 ma postać:
ma postać:
A) 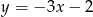 B)
B) 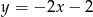 C)
C) 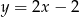 D)
D) 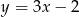
Wskaż wzór funkcji, której wykres przedstawiono na poniższym rysunku.
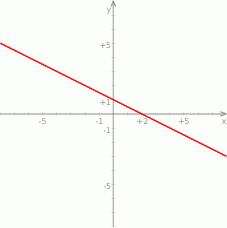
A) 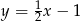 B)
B) 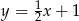 C)
C) 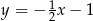 D)
D) 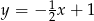
Obwód trójkąta równobocznego 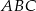 jest równy 12 cm. Punkty
jest równy 12 cm. Punkty 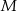 ,
, 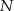 i
i 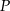 należą odpowiednio do boków
należą odpowiednio do boków 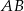 ,
, 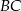 ,
, 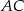 tego trójkąta przy czym
tego trójkąta przy czym 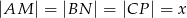 . Zbadaj dla jakiej wartości
. Zbadaj dla jakiej wartości  , pole trójkąta
, pole trójkąta 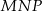 będzie najmniejsze. Znajdź wartość tego pola.
będzie najmniejsze. Znajdź wartość tego pola.
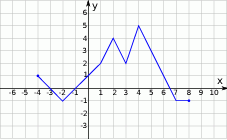
Na rysunku przedstawiono wykres funkcji 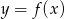 .
.
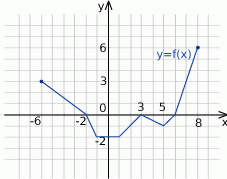
Zbiorem wartości funkcji 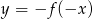 jest
jest
A) 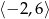 B)
B) 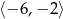 C)
C) 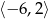 D)
D) 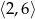
Na rysunku przedstawiono wykres funkcji  .
.
Zbiorem wartości funkcji 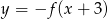 jest
jest
A) 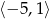 B)
B) 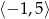 C)
C) 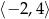 D)
D) 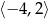
Rozwiąż równanie 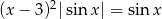 w zbiorze
w zbiorze 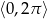 .
.
Naszkicuj wykres funkcji, która każdej liczbie rzeczywistej 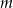 przyporządkowuje liczbę pierwiastków równania
przyporządkowuje liczbę pierwiastków równania
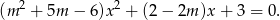
Wyznacz równanie symetralnej odcinka o końcach 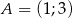 i
i 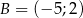 .
.
Wyznacz równanie symetralnej odcinka 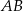 , gdzie
, gdzie 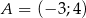 i
i 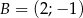 .
.
Wyznacz równanie symetralnej odcinka o końcach 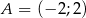 i
i 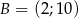 .
.
Wyznacz równanie symetralnej odcinka o końcach 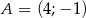 i
i 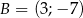 .
.
Wyznacz równanie symetralnej odcinka o końcach 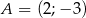 i
i 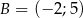 .
.
Wielomian 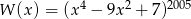 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 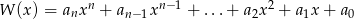 . Oblicz sumę
. Oblicz sumę 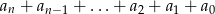 .
.
Wielomian 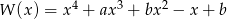 przy dzieleniu przez każdy z dwumianów:
przy dzieleniu przez każdy z dwumianów: 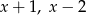 i
i 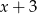 daję tę samą resztę. Wyznacz
daję tę samą resztę. Wyznacz  i
i 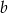 .
.
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 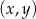 , dane są punkty
, dane są punkty 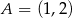 i
i 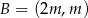 , gdzie
, gdzie 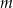 jest liczbą rzeczywistą, oraz prosta
jest liczbą rzeczywistą, oraz prosta 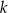 o równaniu
o równaniu 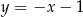 . Prosta przechodząca przez punkty
. Prosta przechodząca przez punkty 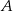 i
i 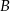 jest prostopadła do prostej
jest prostopadła do prostej 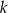 , gdy
, gdy
A) 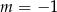 B)
B) 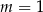 C)
C) 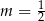 D)
D) 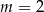
Dany jest odcinek o końcach 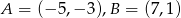 .
.
- Wyznacz równanie symetralnej tego odcinka.
- Wyznacz równanie okręgu o średnicy
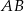 .
.
Dany jest odcinek o końcach 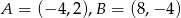 .
.
- Wyznacz równanie okręgu o średnicy
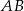 .
. - Wyznacz równanie średnicy prostopadłej do średnicy
 .
.
W pojemniku ze słodyczami znajduje się 48 cukierków i 32 lizaki. Osiem lizaków i piętnaście cukierków ma smak jabłkowy, a pozostałe słodycze mają smak pomarańczowy. Z pojemnika wybrano losowo jeden słodycz (cukierek lub lizak) i okazało się, że ma smak pomarańczowy. Oblicz prawdopodobieństwo zdarzenia, że wybrany słodycz jest lizakiem.

