Dany jest zbiór wszystkich dwucyfrowych liczb naturalnych. Oblicz prawdopodobieństwo, że losowo wybrana z tego zbioru liczba jest podzielna przez 6 lub przez 8.
/Szkoła średnia
Ze zbioru liczb naturalnych dwucyfrowych losowo wybieramy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 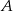 polegającego na tym, że otrzymamy liczbę podzielną przez 9 lub liczbę podzielną przez 12.
polegającego na tym, że otrzymamy liczbę podzielną przez 9 lub liczbę podzielną przez 12.
Ze zbioru liczb naturalnych dwucyfrowych losowo wybieramy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 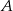 polegającego na tym, że otrzymamy liczbę podzielną przez 6 lub liczbę podzielną przez 9.
polegającego na tym, że otrzymamy liczbę podzielną przez 6 lub liczbę podzielną przez 9.
Ze zbioru liczb naturalnych dwucyfrowych losowo wybieramy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 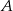 polegającego na tym, że otrzymamy liczbę podzielną przez 8 lub liczbę podzielną przez 12.
polegającego na tym, że otrzymamy liczbę podzielną przez 8 lub liczbę podzielną przez 12.
Wykaż, że jeżeli 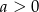 , to
, to 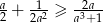 .
.
Wykaż, że jeżeli 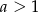 , to
, to 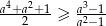 .
.
Ze zbioru liczb 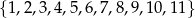 wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 3 lub przez 2.
wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 3 lub przez 2.
Jedną z liczb, które spełniają nierówność 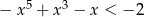 , jest
, jest
A) 1 B) 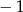 C) 2 D)
C) 2 D) 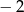
Jedną z liczb spełniających nierówność 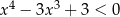 jest
jest
A) 1 B) 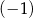 C) 2 D)
C) 2 D) 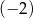
Jedną z liczb, które spełniają nierówność 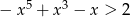 , jest
, jest
A) 1 B) 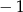 C) 2 D)
C) 2 D) 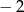
Jedną z liczb spełniających nierówność 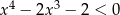 jest
jest
A) 3 B) 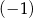 C) 2 D)
C) 2 D) 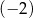
Pole powierzchni bocznej stożka jest cztery razy większe od pola podstawy. Obwód przekroju osiowego stożka jest równy 30. Oblicz objętość tego stożka
Pole powierzchni bocznej stożka jest trzy razy większe od pola jego podstawy. Wysokość tego stożka jest równa 12. Oblicz objętość tego stożka.
Wyznacz takie liczby  i
i 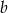 , dla których układ równań
, dla których układ równań 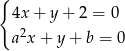 jest sprzeczny, zaś układ równań
jest sprzeczny, zaś układ równań 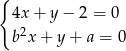 ma nieskończenie wiele rozwiązań.
ma nieskończenie wiele rozwiązań.
Wyznacz wszystkie wartości parametru 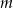 , dla których równanie
, dla których równanie 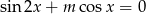 ma w przedziale
ma w przedziale 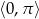 trzy rozwiązania.
trzy rozwiązania.
Wyznacz te wartości parametru 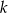 , dla których równanie
, dla których równanie 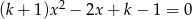 ma dwa różne rozwiązania należące do przedziału
ma dwa różne rozwiązania należące do przedziału 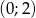 .
.
O zdarzeniach 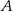 i
i 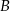 wiadomo, że
wiadomo, że 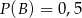 ;
; 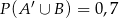 ;
; 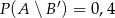 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 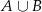 .
.
O zdarzeniach 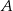 i
i 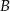 wiadomo, że
wiadomo, że 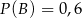 ;
; 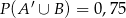 ;
; 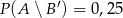 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 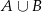 .
.
Funkcja 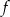 określona jest wzorem
określona jest wzorem 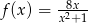 .
.
- Wykaż, że funkcja
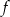 jest nieparzysta.
jest nieparzysta. - Wykaż (z definicji), że funkcja
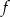 w przedziale
w przedziale 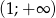 jest malejąca.
jest malejąca. - Wykaż, że funkcja
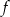 nie przyjmuje wartości większych od 4.
nie przyjmuje wartości większych od 4.
Punkty 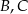 i
i 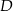 leżą na okręgu o środku
leżą na okręgu o środku 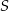 i promieniu
i promieniu  . Punkt
. Punkt 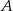 jest punktem wspólnym prostych
jest punktem wspólnym prostych 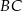 i
i 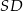 , a odcinki
, a odcinki 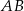 i
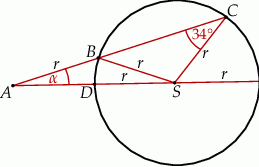
i 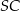 są równej długości. Miara kąta
są równej długości. Miara kąta 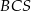 jest równa
jest równa 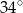 (zobacz rysunek). Wtedy
(zobacz rysunek). Wtedy
A) 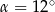 B)
B) 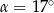 C)
C) 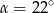 D)
D) 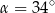
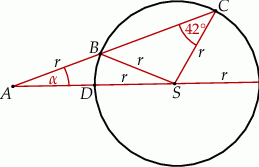
Punkty 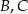 i
i 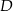 leżą na okręgu o środku
leżą na okręgu o środku 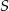 i promieniu
i promieniu  . Punkt
. Punkt 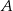 jest punktem wspólnym prostych
jest punktem wspólnym prostych 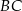 i
i 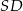 , a odcinki
, a odcinki 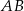 i
i 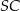 są równej długości. Miara kąta
są równej długości. Miara kąta 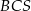 jest równa
jest równa 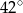 (zobacz rysunek). Wtedy
(zobacz rysunek). Wtedy
A) 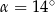 B)
B) 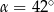 C)
C) 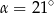 D)
D) 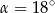
Punkty 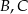 i
i 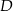 leżą na okręgu o środku
leżą na okręgu o środku 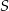 i promieniu
i promieniu  . Punkt
. Punkt 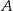 jest punktem wspólnym prostych
jest punktem wspólnym prostych 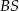 i
i 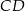 , a odcinki
, a odcinki 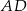 i
i 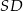 są równej długości. Miara kąta
są równej długości. Miara kąta 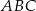 jest równa
jest równa 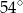 (zobacz rysunek). Wtedy
(zobacz rysunek). Wtedy
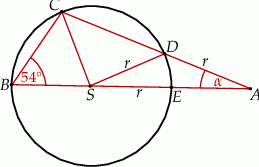
A) 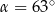 B)
B) 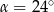 C)
C) 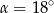 D)
D) 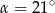
Dla każdej liczby rzeczywistej 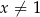 wyrażenie
wyrażenie 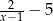 jest równe
jest równe
A) 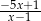 B)
B) 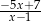 C)
C) 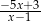 D)
D) 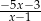
Dla każdej liczby rzeczywistej  różnej od 0 wartość wyrażenia
różnej od 0 wartość wyrażenia 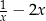 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A)  B)
B) 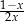 C)
C) 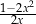 D)
D) 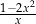
Dla każdej liczby rzeczywistej  różnej od 0 wartość wyrażenia
różnej od 0 wartość wyrażenia 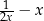 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A)  B)
B) 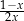 C)
C) 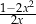 D)
D) 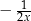
Dla każdej liczby rzeczywistej 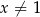 wyrażenie
wyrażenie 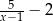 jest równe
jest równe
A) 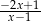 B)
B) 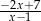 C)
C) 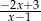 D)
D) 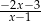
Średnia arytmetyczna cen sześciu akcji na giełdzie jest równa 500 zł. Za pięć z tych akcji zapłacono 2300 zł. Cena szóstej akcji jest równa
A) 400 zł B) 500 zł C) 600 zł D) 700 zł
Kamil ma trzy siostry i jednego brata bliźniaka. Średnia wieku wszystkich dzieci w tej rodzinie jest równa 10,2 roku, a średnia wieku samych dziewcząt jest równa 7 lat. Ile lat ma Kamil?
A) 30 B) 17 C) 15 D) 21
Ala kupiła trzy zeszyty i blok rysunkowy. Średnia arytmetyczna cen tych czterech artykułów była równa 6 zł. Zeszyty kosztowały łącznie 15 zł. Ile kosztował blok rysunkowy?
A) 4 zł B) 5 zł C) 8 zł D) 9 zł
Średnia arytmetyczna cen ośmiu akcji na giełdzie jest równa 600 zł. Za siedem z tych akcji zapłacono 4200 zł. Cena ósmej akcji jest równa
A) 400 zł B) 500 zł C) 600 zł D) 700 zł
Państwo Nowakowie mają trzy córki i jednego syna. Średnia wieku wszystkich dzieci państwa Nowaków jest równa 10 lat, a średnia wieku wszystkich córek jest równa 8 lat. Ile lat ma syn państwa Nowaków?
A) 9 B) 11 C) 12 D) 16
Średnia cena sześciu kartonów mleka po 3,2 zł za karton i dwóch identycznych pojemników śmietany wynosi 2,85 zł. Cena jednego pojemnika śmietany jest równa
A) 1,8 zł B) 3,6 zł C) 2 zł D) 2,4 zł
Średnia arytmetyczna cen dziewięciu akcji na giełdzie jest równa 680 zł. Za osiem z tych akcji zapłacono 5500 zł. Cena dziewiątej akcji jest równa
A) 660 zł B) 580 zł C) 620 zł D) 760 zł
Kasia kupiła cztery ołówki i długopis. Średnia arytmetyczna cen tych pięciu artykułów była równa 1,8 zł. Ołówki kosztowały łącznie 6 zł. Ile kosztował długopis?
A) 2,7 zł B) 1,5 zł C) 2 zł D) 3 zł
Funkcja 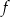 określona jest wzorem
określona jest wzorem
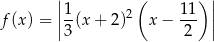
dla każdego 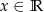 . Pochodna funkcji
. Pochodna funkcji 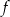 w punkcie
w punkcie 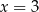 jest równa 0. Wyznacz wszystkie wartości parametru
jest równa 0. Wyznacz wszystkie wartości parametru 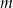 , dla których równanie
, dla których równanie 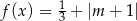 ma cztery rozwiązania, których iloczyn jest ujemny.
ma cztery rozwiązania, których iloczyn jest ujemny.
Jeżeli 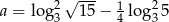 to liczba
to liczba  jest równa
jest równa
A) 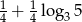 B)
B) 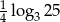 C)
C) 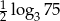 D)
D) 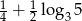
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to 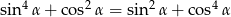 .
.
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to 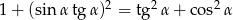 .
.
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to 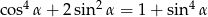 .
.
Niech 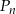 oznacza pole koła o promieniu
oznacza pole koła o promieniu 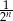 , dla
, dla 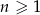 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 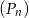 .
.
Niech 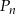 oznacza pole koła o promieniu
oznacza pole koła o promieniu 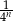 , dla
, dla 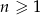 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 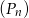 .
.
Niech 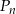 oznacza pole koła o promieniu
oznacza pole koła o promieniu 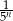 , dla
, dla 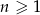 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 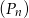 .
.
Niech 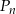 oznacza pole koła o promieniu
oznacza pole koła o promieniu 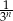 , dla
, dla 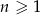 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 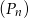 .
.
Liczba rzeczywistych rozwiązań równania 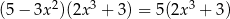 jest równa
jest równa
A) 5 B) 3 C) 2 D) 4
Pole trójkąta wyznaczonego przez wykresy funkcji 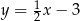 i
i 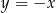 oraz oś
oraz oś 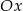 jest równe
jest równe
A) 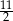 B)
B) 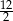 C)
C) 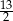 D)
D) 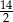
Pole trójkąta wyznaczonego przez wykresy funkcji 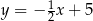 i
i 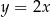 oraz oś
oraz oś 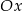 jest równe
jest równe
A) 20 B) 10 C) 32 D) 40
Rozwiąż równanie 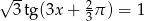 .
.
Rozwiąż równanie 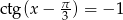 .
.

