Mały Antek założył zeszyt, w którym każdego dnia zapisuje jedną liczbę. Pierwszą zapisaną przez niego liczbą było 112, a każdego następnego dnia zmniejsza wpisywaną liczbę o 7.
- Przez ile dni Antek wpisywał do zeszytu liczby, jeżeli wśród wpisanych liczb są liczby ujemne, a suma wszystkich liczb wynosi 805.
- Ile liczb dodatnich jest wpisanych do zeszytu?

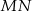 z okręgiem
z okręgiem 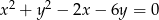 jeśli
jeśli 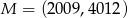 oraz
oraz 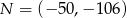 .
. 
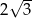
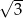
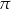
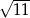
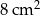 . Dwa boki tego trójkąta mają długości 4 cm i 5 cm. Oblicz długość trzeciego boku tego trójkąta.
. Dwa boki tego trójkąta mają długości 4 cm i 5 cm. Oblicz długość trzeciego boku tego trójkąta.  , dla których ciąg
, dla których ciąg 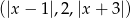 jest malejącym ciągiem arytmetycznym.
jest malejącym ciągiem arytmetycznym. 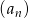 o wyrazie ogólnym
o wyrazie ogólnym 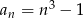 , gdzie
, gdzie 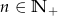 . Wówczas:
. Wówczas: 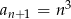
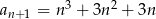
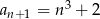
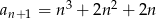
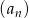 o wyrazie ogólnym
o wyrazie ogólnym 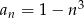 , gdzie
, gdzie 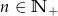 . Wówczas:
. Wówczas: 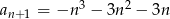
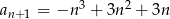
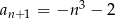
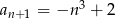
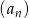 o wyrazie ogólnym
o wyrazie ogólnym 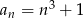 , gdzie
, gdzie 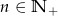 . Wówczas:
. Wówczas: 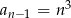
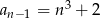
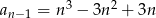
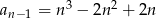
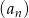 mamy
mamy 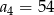 i
i 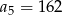 . Wtedy wyraz
. Wtedy wyraz 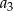 jest równy
jest równy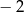 , to drugi wyraz jest równy
, to drugi wyraz jest równy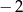
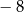
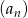 , w którym
, w którym 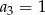 i
i 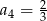 . Wtedy
. Wtedy 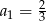
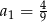
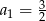
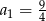
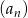 , w którym
, w którym 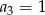 i
i 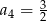 . Wtedy
. Wtedy 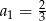
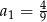
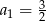
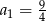
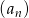 , gdzie
, gdzie 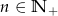 dane są:
dane są: 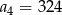 i
i 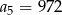 . Zatem:
. Zatem: 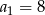
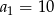
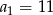
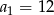
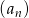 mamy
mamy 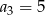 i
i 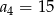 . Wtedy wyraz
. Wtedy wyraz 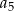 jest równy
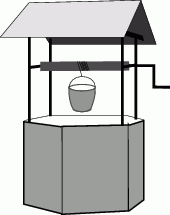
jest równy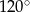 , a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy 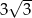
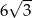
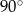 , a tworząca tego stożka ma długość 8. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 8. Promień podstawy stożka jest równy 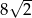
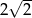
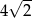
 , jeśli
, jeśli 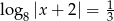 .
. 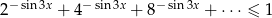 , gdzie
, gdzie 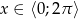 .
. 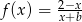 przyjmuje wartości ujemne wtedy i tylko wtedy gdy
przyjmuje wartości ujemne wtedy i tylko wtedy gdy 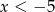 lub
lub 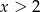 .
. 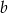 .
. 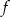 w postaci kanonicznej.
w postaci kanonicznej. 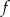 osiąga wartości nie większe niż funkcja
osiąga wartości nie większe niż funkcja 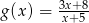 .
.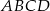 mają długości
mają długości 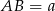 i
i 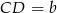 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 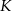 i
i 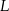 w ten sposób, że odcinek
w ten sposób, że odcinek 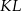 jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka
jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka 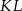 .
. 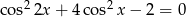 w zbiorze
w zbiorze 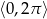 .
. 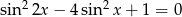 w przedziale
w przedziale 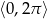 .
. 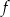 danej wzorem
danej wzorem 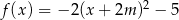 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 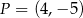 . Wówczas
. Wówczas 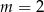
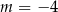
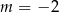
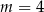
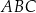 są zawarte w prostych
są zawarte w prostych 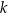 i
i 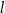 o równaniach
o równaniach 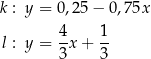
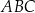
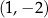
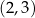

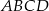 dane są wierzchołki
dane są wierzchołki 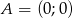 ,
, 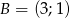 ,
, 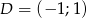 . Wyznacz wierzchołek
. Wyznacz wierzchołek 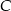 oraz środek symetrii tego równoległoboku.
oraz środek symetrii tego równoległoboku. 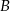 równoległoboku
równoległoboku 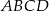 jeżeli
jeżeli 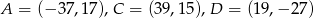 .
. 