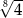Ciąg arytmetyczny składa się z szesnastu wyrazów. Suma wyrazów o numerach parzystych jest równa 256, a suma wyrazów o numerach nieparzystych jest równa 240. Oblicz pierwszy i ostatni wyraz tego ciągu.
/Szkoła średnia
W ciągu arytmetycznym 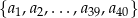 suma wyrazów tego ciągu o numerach parzystych jest równa 1340, a suma wyrazów ciągu o numerach nieparzystych jest równa 1400. Wyznacz ostatni wyraz tego ciągu arytmetycznego.
suma wyrazów tego ciągu o numerach parzystych jest równa 1340, a suma wyrazów ciągu o numerach nieparzystych jest równa 1400. Wyznacz ostatni wyraz tego ciągu arytmetycznego.
W ciągu arytmetycznym 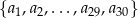 suma wyrazów tego ciągu o numerach parzystych jest równa 555, a suma wyrazów ciągu o numerach nieparzystych jest równa 615. Wyznacz ostatni wyraz tego ciągu arytmetycznego.
suma wyrazów tego ciągu o numerach parzystych jest równa 555, a suma wyrazów ciągu o numerach nieparzystych jest równa 615. Wyznacz ostatni wyraz tego ciągu arytmetycznego.
O pewnym ciągu arytmetycznym wiadomo, że ma dziesięć wyrazów. Suma jego wyrazów o numerach nieparzystych jest równa 75, a suma wyrazów o numerach parzystych jest równa 90. Wyznacz pierwszy wyraz tego ciągu.
Udowodnij, że jeżeli 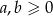 , to prawdziwa jest nierówność
, to prawdziwa jest nierówność 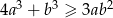 .
.
Wykaż, że dla dowolnych nieujemnych liczb rzeczywistych  ,
, 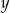 spełniona jest nierówność:
spełniona jest nierówność: 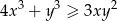 .
.
Uzasadnij, że jeżeli 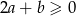 , to
, to 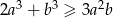 .
.
Wykonując rozmowę telefoniczną płacimy 63 grosze za rozpoczęcie połączenia oraz 42 grosze za każdą minutę połączenia. Ile minut trwała rozmowa, której łączny koszt wyniósł 16,17 zł?
A) 38 B) 36 C) 43 D) 37
Wykonując rozmowę telefoniczną płacimy 43 grosze za rozpoczęcie połączenia oraz 32 grosze za każdą minutę połączenia. Ile minut trwała rozmowa, której łączny koszt wyniósł 12,59 zł?
A) 39 B) 37 C) 38 D) 44
Ostrokątny trójkąt równoramienny 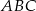 o podstawie
o podstawie 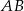 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 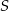 , przy czym kąt
, przy czym kąt 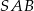 ma miarę
ma miarę 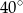 . Oblicz miarę kąta
. Oblicz miarę kąta 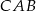 .
.
Wyznacz dziedzinę i zbiór wartości funkcji
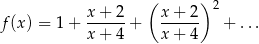
Naszkicuj wykres funkcji 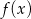 .
.
Oblicz, ile jest liczb naturalnych pięciocyfrowych, w zapisie których nie występuje zero, jest dokładnie jedna cyfra 7 i dokładnie jedna cyfra parzysta.
Oblicz, ile jest czterocyfrowych liczb naturalnych parzystych, w których występuje dokładnie jedno zero.
Oblicz, ile jest liczb naturalnych sześciocyfrowych, w zapisie których występuje dokładnie jedno 0, jest dokładnie jedna cyfra 6 i dokładnie jedna cyfra nieparzysta.
Na trapezie 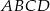 można opisać okrąg. Jedna z jego podstaw jest dwa razy dłuższa od drugiej, a przekątna dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego ple jest równe
można opisać okrąg. Jedna z jego podstaw jest dwa razy dłuższa od drugiej, a przekątna dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego ple jest równe 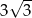 .
.
W kartezjańskim układzie współrzędnych 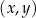 prosta o równaniu
prosta o równaniu 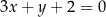 przecina parabolę o równaniu
przecina parabolę o równaniu 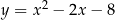 w punktach
w punktach 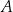 oraz
oraz 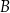 , które są kolejnymi wierzchołkami równoległoboku
, które są kolejnymi wierzchołkami równoległoboku 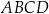 . Wierzchołek
. Wierzchołek 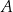 ma pierwszą współrzędną ujemną. Wierzchołek
ma pierwszą współrzędną ujemną. Wierzchołek 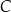 leży na prostej o równaniu
leży na prostej o równaniu 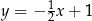 i ma pierwszą współrzędną dodatnią. Odległość punktu
i ma pierwszą współrzędną dodatnią. Odległość punktu 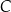 od prostej zawierającej bok
od prostej zawierającej bok 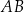 równoległoboku jest równa
równoległoboku jest równa 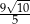 . Oblicz długość boku
. Oblicz długość boku 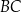 tego równoległoboku.
tego równoległoboku.
W trójkącie równoramiennym o polu 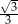 miara kąta przy podstawie jest równa
miara kąta przy podstawie jest równa 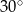 . Długość podstawy tego trójkąta jest liczbą
. Długość podstawy tego trójkąta jest liczbą
A) wymierną mniejszą od 2 B) niewymierną większą o 1
C) całkowitą większą od 1 D) niewymierną mniejszą od 2
W trójkącie równoramiennym o polu 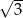 miara kąta przy podstawie jest równa
miara kąta przy podstawie jest równa 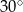 . Długość podstawy tego trójkąta jest liczbą
. Długość podstawy tego trójkąta jest liczbą
A) wymierną mniejszą od 3 B) niewymierną większą o 3
C) całkowitą większą od 3 D) niewymierną mniejszą od 3
W trójkącie równoramiennym o polu 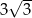 miara kąta przy podstawie jest równa
miara kąta przy podstawie jest równa 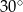 . Długość podstawy tego trójkąta jest liczbą
. Długość podstawy tego trójkąta jest liczbą
A) całkowitą większą od 4 B) niewymierną większą o 4
C) wymierną mniejszą od 4 D) niewymierną mniejszą od 4
Rozwiąż równanie 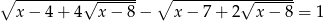 .
.
Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy
A) 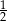 B)
B) 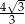 C) 1 D)
C) 1 D) 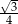
Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 3 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy
A) 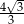 B)
B) 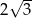 C)
C) 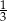 D)
D) 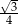
Punkty 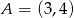 ,
, 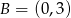 i
i 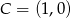 należą do okręgu. Oblicz pole trójkąta równobocznego opisanego na tym okręgu.
należą do okręgu. Oblicz pole trójkąta równobocznego opisanego na tym okręgu.
Nieskończony malejący ciąg geometryczny 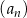 , określony dla
, określony dla 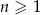 , spełnia warunki:
, spełnia warunki:
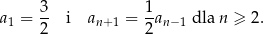
Suma wszystkich wyrazów tego ciągu jest równa
A)  B)
B) 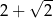 C)
C) 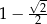 D)
D) 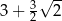
Przyprostokątna trójkąta prostokątnego ma długość 10. Miara kąta ostrego leżącego naprzeciw tej przyprostokątnej wynosi 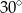 . Oblicz pole koła opisanego na tym trójkącie.
. Oblicz pole koła opisanego na tym trójkącie.
Przyprostokątna trójkąta prostokątnego ma długość 16. Miara kąta ostrego leżącego przy tej przyprostokątnej wynosi 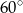 . Oblicz pole koła opisanego na tym trójkącie.
. Oblicz pole koła opisanego na tym trójkącie.
Dane są wielomiany 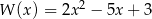 i
i 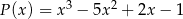 . Wielomian
. Wielomian 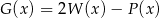 jest równy
jest równy
A) 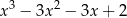 B)
B) 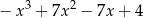
C) 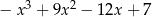 D)
D) 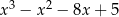
Dane są wielomiany 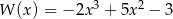 oraz
oraz 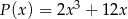 . Wielomian
. Wielomian 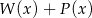 jest równy
jest równy
A) 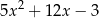 B)
B) 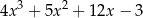
C) 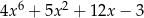 D)
D) 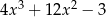
Dane są wielomiany 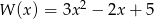 oraz
oraz 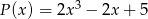 . Wielomian
. Wielomian 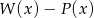 jest równy
jest równy
A) 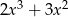 B)
B) 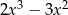 C)
C) 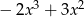 D)
D) 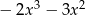
Dane są wielomiany 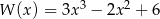 oraz
oraz 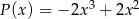 . Wielomian
. Wielomian 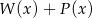 jest równy
jest równy
A) 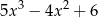 B)
B) 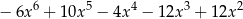
C) 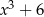 D)
D) 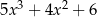
Dane są wielomiany 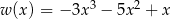 i
i 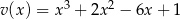 . Wówczas wielomian
. Wówczas wielomian 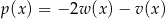 jest równy:
jest równy:
A) 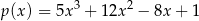 B)
B) 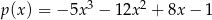
C) 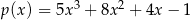 D)
D) 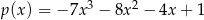
Dane są wielomiany 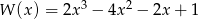 i
i 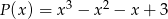 . Wielomian
. Wielomian 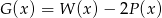 jest równy
jest równy
A) 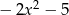 B)
B) 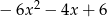 C)
C) 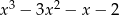 D)
D) 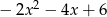
Dane są wielomiany 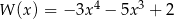 oraz
oraz 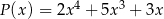 . Wielomian
. Wielomian 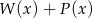 jest równy
jest równy
A) 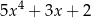 B)
B) 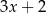
C) 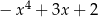 D)
D) 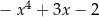
Punkty 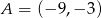 i
i 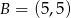 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 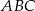 , w którym
, w którym 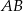 jest przeciwprostokątną. Wyznacz współrzędne wierzchołka
jest przeciwprostokątną. Wyznacz współrzędne wierzchołka 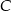 wiedząc, że leży on na osi
wiedząc, że leży on na osi 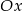 .
.
Punkty 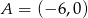 i
i 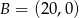 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 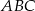 o przeciwprostokątnej
o przeciwprostokątnej 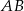 . Wierzchołek
. Wierzchołek 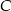 leży na prostej o równaniu
leży na prostej o równaniu 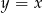 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 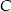 .
.
Punkty 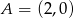 i
i 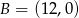 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 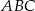 o przeciwprostokątnej
o przeciwprostokątnej 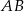 . Wierzchołek
. Wierzchołek 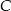 leży na prostej o równaniu
leży na prostej o równaniu 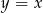 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 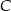 .
.
Oblicz granicę funkcji 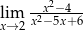 .
.
Oblicz granicę funkcji 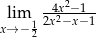 .
.
Wysokość ostrosłupa prawidłowego czworokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość  .
.
Wysokość ostrosłupa prawidłowego czworokątnego jest 2,5 razy dłuższa od krawędzi jego podstawy. Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość  .
.
Liczby dodatnie 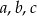 spełniają warunki
spełniają warunki 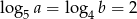 i
i 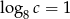 . Wtedy liczba
. Wtedy liczba 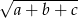 jest równa
jest równa
A) 7 B) 17 C) 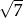 D) 2
D) 2
Liczby dodatnie 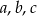 spełniają warunki
spełniają warunki 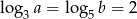 i
i 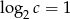 . Wtedy liczba
. Wtedy liczba 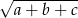 jest równa
jest równa
A) 7 B) 6 C) 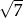 D) 2
D) 2
Liczby dodatnie 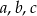 spełniają warunki
spełniają warunki 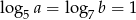 i
i 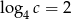 . Wtedy liczba
. Wtedy liczba 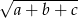 jest równa
jest równa
A) 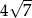 B) 28 C)
B) 28 C) 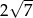 D) 2
D) 2
Liczba 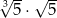 jest równa
jest równa
A) 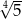 B)
B) 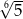 C)
C) 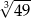 D)
D) 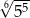
Liczba 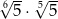 jest równa liczbie
jest równa liczbie
A) 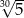 B)
B) 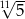 C)
C) 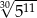 D)
D) 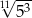
Liczba 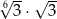 jest równa
jest równa
A) 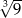 B)
B) 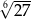 C)
C) 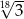 D)
D) 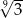
Liczba 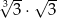 jest równa
jest równa
A) 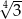 B)
B) 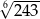 C)
C) 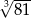 D)
D) 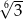
Liczba 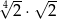 jest równa
jest równa
A) 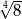 B)
B) 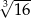 C)
C) 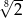 D)
D)