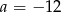Dla której z podanych wartości  , wykres funkcji
, wykres funkcji 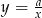 nie ma punktów wspólnych z wykresem funkcji
nie ma punktów wspólnych z wykresem funkcji 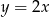 ?
?
A) 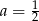 B)
B) 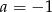 C)
C) 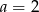 D)
D) 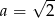
/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Homografia
Do wykresu funkcji 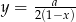 dla
dla 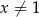 należy punkt
należy punkt 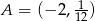 . Wtedy
. Wtedy
A) 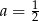 B)
B) 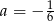 C)
C) 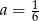 D)
D) 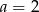
Wykres funkcji 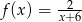 powstaje przez przesunięcie wykresu funkcji
powstaje przez przesunięcie wykresu funkcji 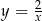 o 6 jednostek
o 6 jednostek
A) w lewo B) w prawo C) w górę D) w dół
Aby otrzymać wykres funkcji 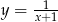 należy wykres funkcji
należy wykres funkcji 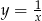 przesunąć o 1 jednostkę
przesunąć o 1 jednostkę
A) w dół B) w górę C) w prawo D) w lewo
Wykres funkcji 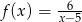 powstaje przez przesunięcie wykresu funkcji
powstaje przez przesunięcie wykresu funkcji 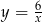 o 5 jednostek
o 5 jednostek
A) w lewo B) w prawo C) w górę D) w dół
Wykres funkcji 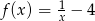 powstaje przez przesunięcie wykresu funkcji
powstaje przez przesunięcie wykresu funkcji 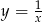 o 4 jednostki
o 4 jednostki
A) w lewo B) w prawo C) w górę D) w dół
Zbiorem wartości funkcji 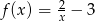 jest
jest
A) 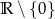 B)
B) 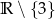 C)
C) 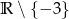 D)
D) 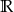
Zbiorem wartości funkcji 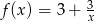 jest
jest
A) 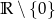 B)
B) 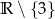 C)
C) 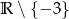 D)
D) 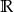
Zbiorem wartości funkcji 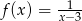 jest
jest
A) 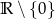 B)
B) 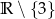 C)
C) 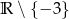 D)
D) 
Do wykresu funkcji 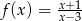 należy punkt
należy punkt
A) 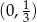 B)
B) 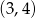 C)
C) 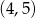 D)
D) 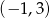
Do wykresu funkcji 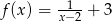 , należy punkt o współrzędnych:
, należy punkt o współrzędnych:
A) 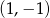 B)
B) 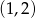 C)
C) 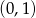 D)
D) 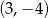
Do wykresu funkcji 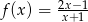 należy punkt
należy punkt
A) 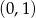 B)
B) 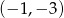 C)
C) 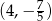 D)
D) 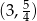
Wykres funkcji 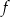 przedstawionej na rysunku powstał przez przesunięcie wykresu funkcji
przedstawionej na rysunku powstał przez przesunięcie wykresu funkcji 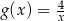 wzdłuż osi odciętych.
wzdłuż osi odciętych.
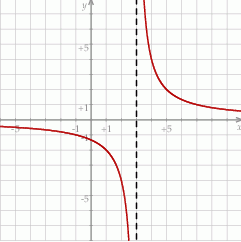
Funkcja 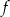 jest określona wzorem
jest określona wzorem
A) 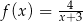 B)
B) 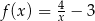 C)
C) 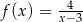 D)
D) 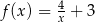
Wykres funkcji 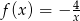 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 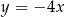 B)
B) 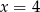 C)
C) 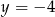 D)
D) 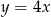
Wykres funkcji 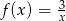 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 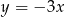 B)
B) 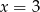 C)
C) 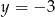 D)
D) 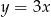
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 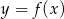 , której dziedziną jest zbiór
, której dziedziną jest zbiór 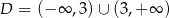 .
.
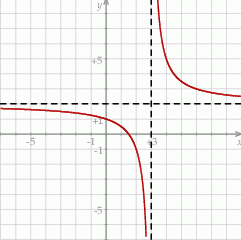
Równanie 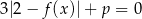 z niewiadomą
z niewiadomą  ma dokładnie dwa rozwiązania tylko wtedy, gdy
ma dokładnie dwa rozwiązania tylko wtedy, gdy
A) 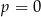 B)
B) 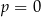 lub
lub 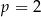 C)
C) 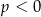 D)
D) 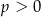
Wykres funkcji 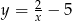 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 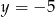 B)
B) 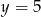 C)
C) 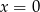 D)
D) 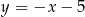
Wykres funkcji 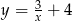 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 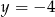 B)
B) 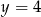 C)
C) 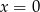 D)
D) 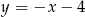
Wykres funkcji 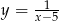 ma jeden punkt wspólny z prostą o równaniu
ma jeden punkt wspólny z prostą o równaniu
A) 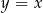 B)
B) 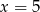 C)
C) 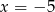 D)
D) 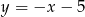
Do wykresu funkcji 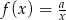 należy punkt o współrzędnych
należy punkt o współrzędnych 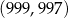 . Zatem funkcja
. Zatem funkcja 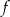
A) jest rosnąca na przedziale 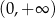 B) jest malejąca na przedziale
B) jest malejąca na przedziale 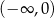
C) nie przyjmuje wartości dodatnich D) jest rosnąca w zbiorze 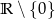
Do wykresu funkcji 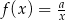 należy punkt o współrzędnych
należy punkt o współrzędnych 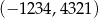 . Zatem funkcja
. Zatem funkcja 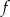
A) jest rosnąca na przedziale 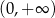 B) jest malejąca na przedziale
B) jest malejąca na przedziale 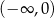
C) nie przyjmuje wartości dodatnich D) jest rosnąca w zbiorze 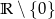
Styczna do wykresu funkcji 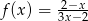 w punkcie o współrzędnych
w punkcie o współrzędnych 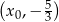 ma równanie
ma równanie
A) 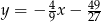 B)
B) 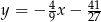 C)
C) 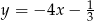 D)
D) 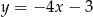
Do wykresu funkcji 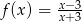 należy punkt
należy punkt
A) 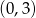 B)
B) 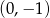 C)
C) 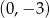 D)
D) 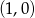
Do wykresu funkcji 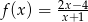 należy punkt
należy punkt
A) 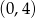 B)
B) 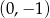 C)
C) 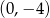 D)
D) 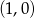
Przedstawiony na rysunku wykres może być wykresem funkcji
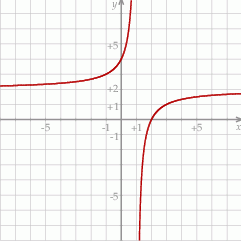
A) 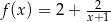 B)
B) 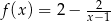 C)
C) 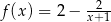 D)
D) 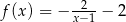
Przedstawiony na rysunku wykres może być wykresem funkcji
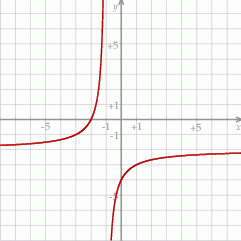
A) 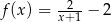 B)
B) 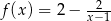 C)
C) 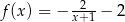 D)
D) 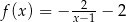
Wykres funkcji 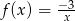 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i IV B) II i III C) I i III D) I i II
Wykres funkcji 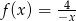 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) I i II B) II i III C) I i III D) II i IV
Wykres funkcji 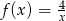 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i IV B) II i III C) I i III D) I i II
Wykres funkcji 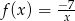 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i III B) II i IV C) I i III D) I i II
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 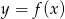 , której dziedziną jest zbiór
, której dziedziną jest zbiór 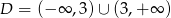 .
.
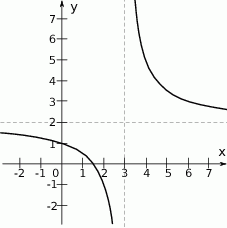
Równanie 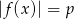 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie
A) w dwóch przypadkach: 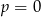 lub
lub 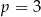 .
.
B) w dwóch przypadkach: 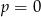 lub
lub 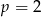 .
.
C) tylko wtedy, gdy 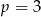 .
.
D) tylko wtedy, gdy 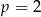 .
.
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 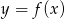 , której dziedziną jest zbiór
, której dziedziną jest zbiór 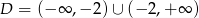 .
.
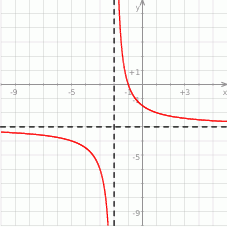
Równanie 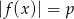 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie
A) w dwóch przypadkach: 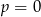 lub
lub 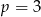 .
.
B) w dwóch przypadkach: 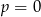 lub
lub 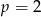 .
.
C) tylko wtedy, gdy 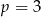 .
.
D) tylko wtedy, gdy 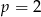 .
.
Do wykresu funkcji 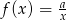 , dla
, dla 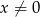 należy punkt
należy punkt 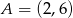 . Wtedy
. Wtedy
A) 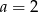 B)
B) 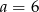 C)
C) 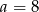 D)
D) 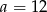
Do wykresu funkcji 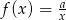 , dla
, dla 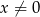 należy punkt
należy punkt 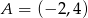 . Wtedy
. Wtedy
A) 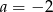 B)
B) 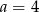 C)
C) 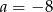 D)
D)