Dla jakich wartości parametru 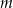 równanie
równanie 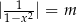 ma trzy rozwiązania?
ma trzy rozwiązania?
/Szkoła średnia/Równania/Z wartością bezwględną
Wyznacz wszystkie wartości parametru 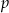 , dla których równanie
, dla których równanie 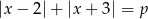 ma dokładnie dwa rozwiązania.
ma dokładnie dwa rozwiązania.
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 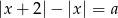 nie ma rozwiązania.
nie ma rozwiązania.
Dla jakich wartości parametru 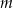 równanie
równanie 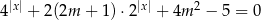 ma tylko jedno rozwiązanie?
ma tylko jedno rozwiązanie?
Zbadaj dla jakich wartości parametru 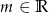 równanie
równanie 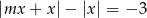 ma rozwiązanie.
ma rozwiązanie.
Wyznacz te wartości parametru 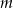 , dla których równanie
, dla których równanie 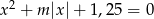 ma cztery rozwiązania.
ma cztery rozwiązania.
Rozwiąż równanie 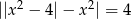 .
.
Naszkicuj wykres funkcji 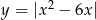 . Na podstawie wykresu określ dla jakich
. Na podstawie wykresu określ dla jakich 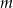 równanie
równanie 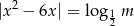 ma co najmniej 3 rozwiązania.
ma co najmniej 3 rozwiązania.
Rozwiąż równanie 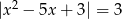 .
.
Zbadaj liczbę rozwiązań równania 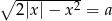 w zależności od wartości parametru
w zależności od wartości parametru  .
.
Rozwiąż równanie 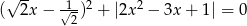 .
.
Funkcja 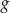 jest określona wzorem
jest określona wzorem 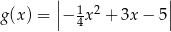 dla każdego
dla każdego 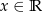 . Fragment wykresu funkcji
. Fragment wykresu funkcji 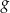 w kartezjańskim układzie współrzędnych
w kartezjańskim układzie współrzędnych 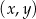 przedstawiono na rysunku (jednostki pominięto).
przedstawiono na rysunku (jednostki pominięto).
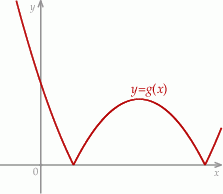
Wyznacz zbiór wszystkich wartości parametru 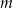 , dla których równanie
, dla których równanie 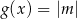 ma dokładnie dwa rozwiązania dodatnie.
ma dokładnie dwa rozwiązania dodatnie.
Funkcja 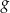 jest określona wzorem
jest określona wzorem 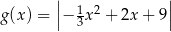 dla każdego
dla każdego 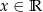 . Fragment wykresu funkcji
. Fragment wykresu funkcji 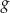 w kartezjańskim układzie współrzędnych
w kartezjańskim układzie współrzędnych 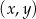 przedstawiono na rysunku (jednostki pominięto).
przedstawiono na rysunku (jednostki pominięto).
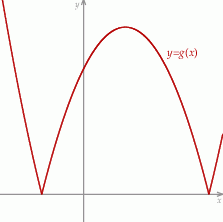
Wyznacz zbiór wszystkich wartości parametru 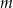 , dla których równanie
, dla których równanie 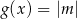 ma dokładnie dwa rozwiązania dodatnie.
ma dokładnie dwa rozwiązania dodatnie.
Rozwiąż równanie 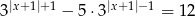 .
.
Rozwiąż równanie 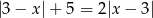 .
.
Wyznacz wszystkie wartości parametru 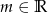 , dla których równanie
, dla których równanie 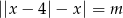 ma tylko jedno rozwiązanie.
ma tylko jedno rozwiązanie.
Wyznacz wszystkie wartości parametru 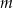 , dla których równanie
, dla których równanie
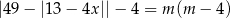
ma cztery różne rozwiązania, których iloczyn jest ujemny.
Zbadaj dla jakich wartości parametru 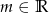 równanie
równanie 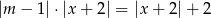 ma rozwiązanie.
ma rozwiązanie.
Rozwiąż algebraicznie i graficznie układ równań 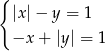 .
.
Zbadaj liczbę rozwiązań układu równań w zależności od parametru 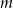
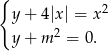
Rozwiąż równanie 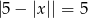 .
.
Podaj liczbę rozwiązań równania 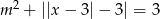 w zależności od wartości parametru
w zależności od wartości parametru 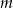 .
.

