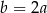Jeśli 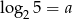 oraz
oraz 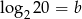 , to liczba
, to liczba 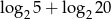 jest równa
jest równa
A) 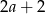 B)
B) 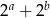 C)
C) 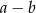 D)
D) 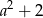
/Szkoła średnia/Zadania testowe/Liczby/Logarytmy/Z literkami
Jeśli 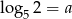 oraz
oraz 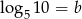 , to liczba
, to liczba 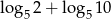 jest równa
jest równa
A) 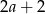 B)
B) 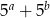 C)
C) 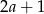 D)
D) 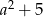
Jeżeli 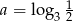 i
i 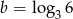 , to liczba
, to liczba  jest równa
jest równa
A) 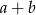 B)
B) 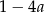 C)
C) 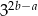 D)
D) 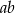
Jeśli 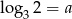 oraz
oraz 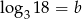 , to liczba
, to liczba 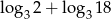 jest równa
jest równa
A) 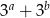 B)
B) 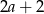 C)
C) 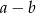 D)
D) 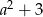
Wiadomo, że 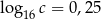 . Zatem liczba
. Zatem liczba  jest
jest
A) niewymierna B) wymierna C) większa od 2 D) mniejsza od 1
Wiadomo, że 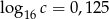 . Zatem liczba
. Zatem liczba  jest
jest
A) niewymierna B) wymierna C) większa od 2 D) mniejsza od 1
Jeśli 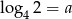 , to liczba
, to liczba  jest równa
jest równa
A) 16 B) 2 C) -2 D) 0,5
Jeżeli 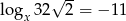 to liczba
to liczba  jest równa
jest równa
A) 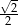 B)
B) 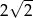 C)
C) 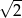 D) 2
D) 2
Jeżeli 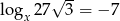 to liczba
to liczba  jest równa
jest równa
A) 3 B) 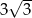 C)
C) 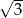 D)
D) 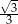
Liczba 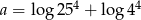 . Wynika stąd, że
. Wynika stąd, że
A) 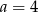 B)
B) 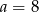 C)
C) 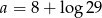 D)
D) 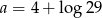
Liczba 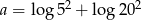 . Wynika stąd, że
. Wynika stąd, że
A) 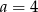 B)
B) 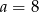 C)
C) 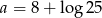 D)
D) 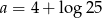
Liczba 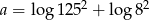 . Wynika stąd, że
. Wynika stąd, że
A) 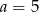 B)
B) 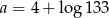 C)
C) 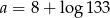 D)
D) 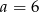
Wiadomo, że 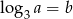 . Wtedy
. Wtedy 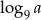 równa się
równa się
A) 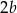 B)
B)  C)
C) 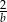 D)
D) 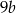
Wiadomo, że 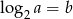 . Wtedy
. Wtedy 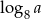 równa się
równa się
A) 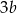 B)
B) 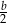 C)
C) 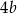 D)
D) 
Wiadomo, że 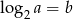 . Wtedy
. Wtedy 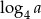 równa się
równa się
A) 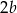 B)
B) 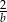 C)
C)  D)
D) 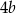
O liczbie  wiadomo, że
wiadomo, że 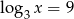 . Zatem
. Zatem
A) 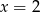 B)
B) 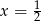 C)
C) 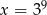 D)
D) 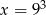
O liczbie  wiadomo, że
wiadomo, że 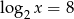 . Zatem
. Zatem
A) 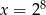 B)
B) 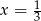 C)
C) 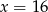 D)
D) 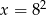
Jeśli 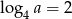 , to liczba
, to liczba  jest równa
jest równa
A) 16 B) 2 C) -2 D) 4
O liczbie  wiadomo, że
wiadomo, że 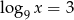 . Zatem
. Zatem
A) 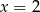 B)
B) 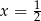 C)
C) 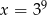 D)
D) 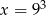
Jeżeli 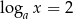 i
i 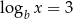 , to liczba
, to liczba 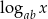 jest równa
jest równa
A) 6 B)  C)
C) 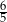 D)
D) 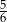
Jeżeli 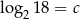 , to liczba
, to liczba 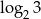 jest równa
jest równa
A) 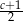 B)
B) 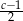 C)
C) 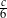 D)
D) 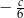
Jeżeli 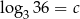 , to liczba
, to liczba 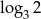 jest równa
jest równa
A) 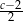 B)
B) 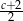 C)
C) 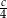 D)
D) 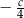
Jeżeli 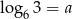 , to
, to 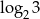 równa się
równa się
A) 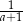 B)
B) 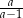 C)
C) 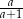 D)
D) 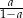
Dane są liczby 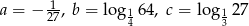 . Iloczyn
. Iloczyn 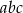 jest równy
jest równy
A) 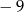 B)
B) 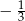 C)
C) 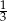 D) 3
D) 3
Dane są liczby 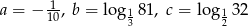 . Iloczyn
. Iloczyn 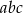 jest równy
jest równy
A) 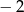 B)
B) 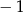 C)
C) 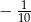 D)
D) 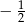
Wiadomo, że 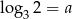 oraz
oraz 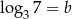 . Zatem
. Zatem 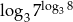 jest równy
jest równy
A) 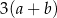 B)
B) 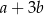 C)
C) 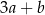 D)
D) 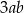
Jeżeli 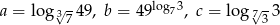 to
to
A) 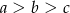 B)
B) 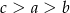 C)
C) 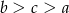 D)
D) 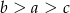
Jeżeli 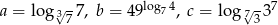 to
to
A) 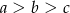 B)
B) 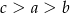 C)
C) 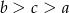 D)
D) 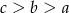
Jeżeli 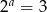 ,
, 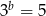 i
i 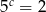 , to iloczyn
, to iloczyn 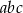 jest równy
jest równy
A) 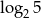 B)
B) 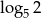 C) 1 D) 2
C) 1 D) 2
Jeżeli 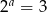 ,
, 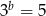 i
i 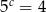 , to iloczyn
, to iloczyn 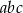 jest równy
jest równy
A) 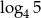 B)
B) 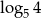 C) 4 D) 2
C) 4 D) 2
Dla dowolnych liczb 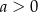 ,
, 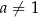 ,
, 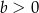 ,
, 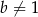 ,
, 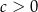 ,
, 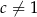 wartość wyrażenia
wartość wyrażenia
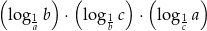
jest równa
A) 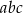 B)
B) 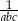 C)
C) 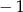 D) 1
D) 1
Dla dowolnej liczby rzeczywistej 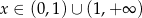 zachodzi zależność
zachodzi zależność 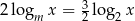 . Wartość parametru
. Wartość parametru 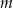 jest równa
jest równa
A)  B)
B) 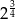 C)
C) 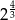 D)
D) 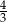
O liczbie dodatniej 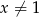 wiadomo, że
wiadomo, że 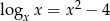 . Zatem
. Zatem
A) 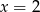 B)
B) 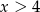 C)
C) 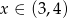 D)
D) 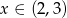
Liczba 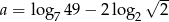 . Wynika z tego, że
. Wynika z tego, że
A) 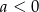 B)
B) 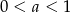 C)
C) 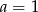 D)
D) 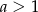
Liczba 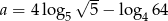 . Wynika z tego, że
. Wynika z tego, że
A) 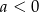 B)
B) 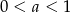 C)
C) 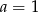 D)
D) 
Liczba 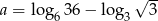 . Wynika z tego, że
. Wynika z tego, że
A) 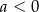 B)
B) 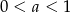 C)
C) 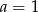 D)
D) 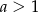
Liczba  jest rozwiązaniem równania
jest rozwiązaniem równania 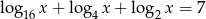 . Zatem
. Zatem
A) 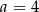 B)
B) 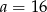 C)
C) 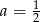 D)
D) 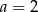
Wiadomo, że 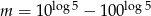 i
i 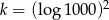 . Zatem
. Zatem
A) 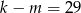 B)
B) 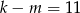 C)
C) 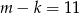 D)
D) 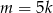
Wiadomo, że 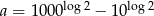 i
i 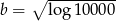 . Zatem
. Zatem
A) 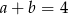 B)
B) 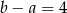 C)
C) 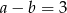 D)
D) 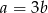
Wiadomo, że 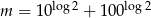 i
i 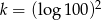 . Zatem
. Zatem
A) 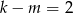 B)
B) 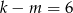 C)
C) 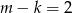 D)
D) 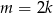
Dane są liczby 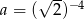 oraz
oraz 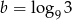 . Zatem
. Zatem
A) 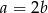 B)
B) 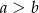 C)
C) 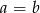 D)
D) 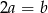
Jeżeli 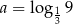 oraz
oraz 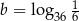 , to
, to
A) 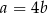 B)
B) 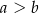 C)
C) 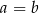 D)
D)