Wykaż, że dla dowolnej liczby rzeczywistej 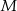 nierówność
nierówność
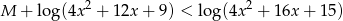
ma przynajmniej jedno rozwiązanie w przedziale 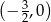 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla dowolnej liczby rzeczywistej 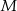 nierówność
nierówność
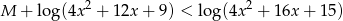
ma przynajmniej jedno rozwiązanie w przedziale 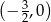 .
.
Wykaż, że jeżeli 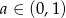 i
i 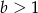 to prawdziwa jest nierówność
to prawdziwa jest nierówność
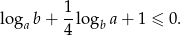
Wykaż, że jeżeli 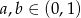 to prawdziwa jest nierówność
to prawdziwa jest nierówność
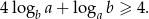
Korzystając z tego, że 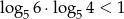 wykaż, że
wykaż, że
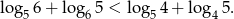
Wykaż, że jeżeli 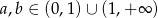 , to
, to
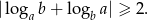
Wykaż, że jeżeli 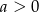 i
i 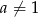 ,
, 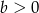 i
i 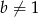 , to
, to 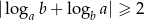 .
.
Wykaż, że jeżeli 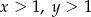 i
i 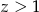 , to
, to 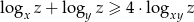 .
.
