Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny opisany na okręgu

Wyszukiwanie zadań

Obwód trapezu równoramiennego opisanego na okręgu jest równy 16, a przekątna trapezu ma długość 5. Oblicz długość promienia okręgu wpisanego w ten trapez i promienia okręgu opisanego na nim.

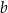Długości podstaw trapezu równoramiennego są równe a oraz b , przy czym 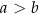a > b . W ten trapez można wpisać okrąg. Wykaż, że pole tego trapezu jest większe od a ⋅b .

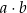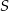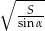Pole trapezu równoramiennego opisanego na okręgu jest równe S , a kąt ostry przy podstawie ma miarę α . Wykaż, że ramię tego trapezu ma długość ∘ ---- -S-- sinα .

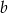Trapez równoramienny o podstawach długości a i b opisany jest na okręgu. Oblicz pole koła, którego brzegiem jest okrąg wpisany w ten trapez.

Punkt styczności okręgu o promieniu r wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 1:2. Oblicz promień okręgu opisanego na tym trapezie.

Ukryj Podobne zadania

Punkt styczności okręgu o promieniu r wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 2:5. Oblicz promień okręgu opisanego na tym trapezie.

Trapez równoramienny jest opisany na okręgu. Obwód trapezu wynosi 16cm, a przekątna ma długość 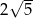√ -- 2 5 . Oblicz długości boków tego trapezu.

W trapez równoramienny o obwodzie 20 i przekątnej długości 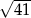√ --- 41 można wpisać okrąg. Oblicz odległości punktu przecięcia przekątnych tego trapezu od prostych zawierających jego boki.

W trapez można wpisać okrąg o promieniu 4 i jednocześnie na tym trapezie można opisać okrąg. Kąt ostry trapezu ma miarę 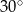30∘ . Oblicz promień okręgu opisanego na tym trapezie.

Ukryj Podobne zadania

W dany trapez można wpisać okrąg i jednocześnie można na tym trapezie opisać okrąg. Wysokość tego trapezu jest równa 8, a jego kąt ostry ma miarę 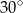30 ∘ . Oblicz długość promienia okręgu opisanego na tym trapezie.

Oblicz długości boków trapezu równoramiennego opisanego na okręgu, znając obwód trapezu 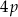4p i długość 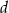d jego przekątnej.

Trapez równoramienny o obwodzie 20 dm i przekątnej długości 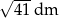√ --- 4 1 dm jest opisany na okręgu. Oblicz jego pole i cosinusy jego kątów wewnętrznych.

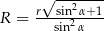Na okręgu o promieniu r opisano trapez równoramienny, którego kąt ostry ma miarę α . Wykaż, że promień okręgu opisanego na tym czworokącie jest równy √ ------- r--sin2α+-1 R = sin2α .

W trapez równoramienny o obwodzie 60 wpisano okrąg. Przekątna trapezu ma długość 17. Oblicz pole trapezu.

Trapez równoramienny 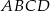ABCD jest opisany na okręgu o promieniu r . Przekątna trapezu tworzy z dłuższą podstawą kąt α . Wyznacz obwód tego trapezu.

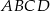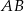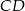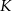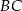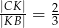Na okręgu o danym promieniu r opisano trapez równoramienny ABCD o dłuższej podstawie AB i krótszej CD . Punkt styczności K dzieli ramię BC tak, że |CK-|= 2 |KB | 3 .

  • Wyznacz długość ramienia tego trapezu.
  • Oblicz cosinus kąta CBD .

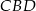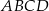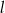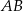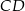Dany jest trapez równoramienny ABCD o obwodzie l i podstawach AB oraz CD takich, że 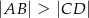|AB | > |CD | . Trapez jest opisany na okręgu i wpisany w okrąg, a przekątna 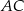AC trapezu ma długość 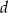d (zobacz rysunek).

PIC

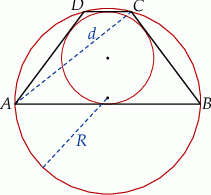
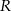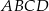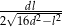Wykaż, że promień R okręgu opisanego na trapezie ABCD jest równy -√--dl---- 2 16d2−l2 .

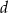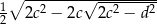Trapez równoramienny o przekątnej długości d i ramieniu długości c jest opisany na okręgu. Wykaż, że odległość środka okręgu wpisanego w ten trapez od końca krótszej podstawy jest równa ∘ ------------------- 1 2c2 − 2c √ 2c2 − d 2 2 .

Trapez równoramienny jest opisany na okręgu. Suma długości krótszej podstawy i ramienia trapezu jest równa 30. Wyraź pole tego trapezu jako funkcję długości jego ramienia. Wyznacz dziedzinę tej funkcji.

Udowodnij, że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średniej geometrycznej długości podstaw trapezu.

Ukryj Podobne zadania

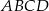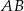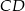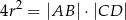Trapez równoramienny ABCD o podstawach AB i CD jest opisany na okręgu o promieniu r . Wykaż, że 4r2 = |AB |⋅|CD | .

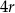Na okręgu o promieniu r opisano trapez równoramienny, którego długość jednej z podstaw wynosi 4r . Oblicz odległość środka okręgu od wierzchołków trapezu.

W trapez równoramienny, który nie jest równoległobokiem, wpisano okrąg promieniu 4 cm. Ramię trapezu ma długość 10 cm. Punkty styczności okręgu z ramionami trapezu dzielą obwód trapezu na dwie częsci. Oblicz stosunek długości tych części.

Strona 1 z 2