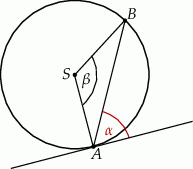
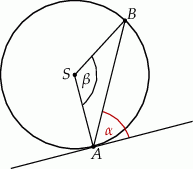
Kąt między cięciwą 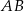 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 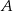 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 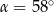 . Wówczas
. Wówczas
A) 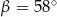 B)
B) 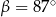 C)
C) 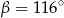 D)
D) 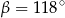
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Kąt między cięciwą 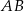 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie  (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 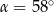 . Wówczas
. Wówczas

A) 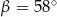 B)
B) 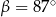 C)
C) 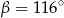 D)
D) 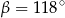
Punkty 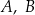 oraz
oraz 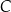 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 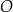 . Prosta
. Prosta 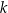 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 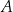 i tworzy z cięciwą
i tworzy z cięciwą 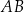 kąt o mierze
kąt o mierze 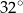 . Ponadto odcinek
. Ponadto odcinek 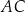 jest średnicą tego okręgu (zobacz rysunek).
jest średnicą tego okręgu (zobacz rysunek).

Miara kąta rozwartego 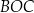 jest równa
jest równa
A) 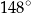 B)
B) 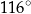 C)
C) 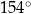 D)
D) 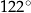
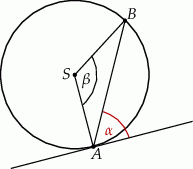
Kąt między cięciwą 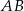 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie  (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 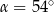 . Wówczas
. Wówczas
A) 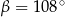 B)
B) 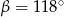 C)
C) 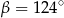 D)
D) 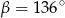
Punkty 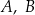 oraz
oraz 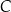 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 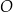 . Prosta
. Prosta 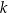 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 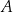 i tworzy z cięciwą
i tworzy z cięciwą 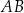 kąt o mierze
kąt o mierze 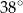 . Ponadto odcinek
. Ponadto odcinek 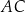 jest średnicą tego okręgu (zobacz rysunek).
jest średnicą tego okręgu (zobacz rysunek).

Miara kąta rozwartego 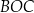 jest równa
jest równa
A) 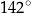 B)
B) 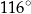 C)
C) 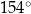 D)
D) 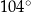
Kąt między cięciwą 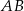 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 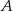 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 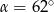 . Wówczas
. Wówczas
A) 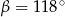 B)
B) 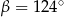 C)
C) 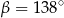 D)
D) 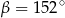
Liczba 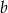 jest 3 razy większa od liczby
jest 3 razy większa od liczby  . Wtedy
. Wtedy
A) 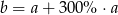 B)
B) 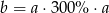 C)
C) 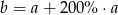 D)
D) 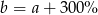
Liczba 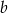 jest 2 razy większa od liczby
jest 2 razy większa od liczby  . Wtedy
. Wtedy
A) 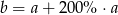 B)
B) 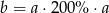 C)
C) 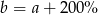 D)
D) 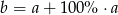
Każdy z dwóch pojemników był początkowo wypełniony 1 kg wodnego roztworu soli o stężeniu 5%. Do pierwszego pojemnika dosypano 150 g soli i dolano 1,55 kg wody. Do drugiego pojemnika dosypano 100 g soli i dolano 0,925 kg wody. Czy stężenie roztworu soli w pojemniku I jest większe niż w pojemniku II? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | stężenia soli w obu pojemnikach są takie same. |
| B) | 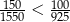 . . |
| C) | 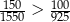 . . |
Kwotę 1000 zł ulokowano w banku na roczną lokatę oprocentowaną w wysokości 4% w stosunku rocznym. Po zakończeniu lokaty od naliczonych odsetek odprowadzany jest podatek w wysokości 19%. Maksymalna kwota, jaką po upływie roku będzie można wypłacić z banku, jest równa
A) 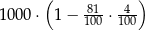 B)
B) 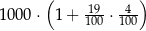
C) 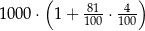 D)
D) 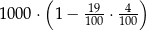
Kwotę 2000 zł ulokowano w banku na roczną lokatę oprocentowaną w wysokości 3% w stosunku rocznym. Po zakończeniu lokaty od naliczonych odsetek odprowadzany jest podatek w wysokości 19%. Maksymalna kwota, jaką po upływie roku będzie można wypłacić z banku, jest równa
A) 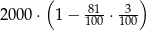 B)
B) 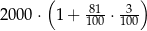
C) 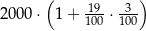 D)
D) 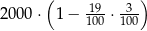
Z jednakowych czworościennych klocków ułożono bryłę mającą kształt czworościanu foremnego.
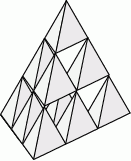
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Utworzona bryła składa się z 10 klocków. | P | F |
| Czworościan foremny o wymiarach takich jak utworzona figura ma objętość 27 razy większą od objętości jednego klocka. | P | F |
Na rysunku przedstawiono prostokąt o bokach długości  i
i  podzielony na sześć kwadratów.
podzielony na sześć kwadratów.
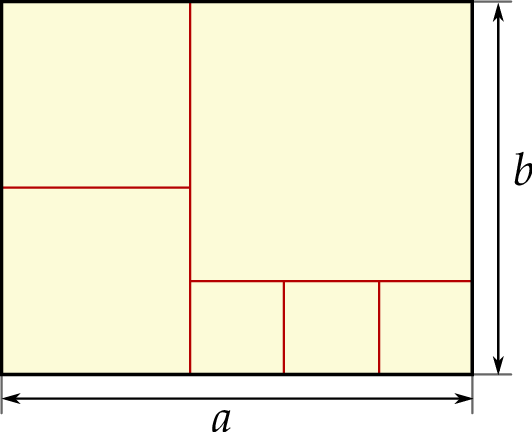
Stosunek długości boków 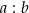 tego prostokąta jest równy
tego prostokąta jest równy
A) 6 : 5 B) 5 : 4 C) 4 : 3 D) 3 : 2
Dany jest wzór na pole powierzchni całkowitej graniastosłupa:
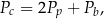
gdzie: 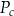 – pole powierzchni całkowitej,
– pole powierzchni całkowitej, 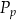 – pole podstawy,
– pole podstawy, 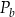 – pole powierzchni bocznej. Pole podstawy
– pole powierzchni bocznej. Pole podstawy 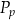 wyznaczone poprawnie z powyższego wzoru opisano równaniem
wyznaczone poprawnie z powyższego wzoru opisano równaniem
A) 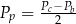 B)
B) 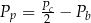 C)
C) 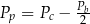 D)
D) 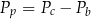
Dany jest wzór na pole powierzchni całkowitej graniastosłupa prawidłowego sześciokątnego:
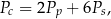
gdzie: 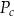 – pole powierzchni całkowitej,
– pole powierzchni całkowitej, 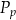 – pole podstawy,
– pole podstawy, 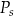 – pole powierzchni jednej ściany bocznej. Pole ściany bocznej
– pole powierzchni jednej ściany bocznej. Pole ściany bocznej 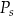 wyznaczone poprawnie z powyższego wzoru opisano równaniem
wyznaczone poprawnie z powyższego wzoru opisano równaniem
A) 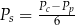 B)
B) 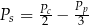 C)
C) 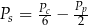 D)
D) 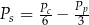
Jacek z 14 jednakowych sześciennych kostek skleił figurę, której widok z przodu i z tyłu przedstawiono na rysunkach.
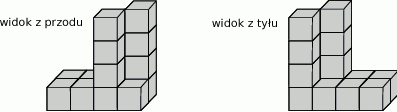
Całą figurę, również od spodu, Jacek pomalował. Ile sześciennych kostek ma pomalowane dokładnie 4 ściany?
A) 8 B) 7 C) 6 D) 5
Dagmara z 20 jednakowych sześciennych kostek skleiła figurę, której widok z przodu i z tyłu przedstawiono na rysunkach.

Całą figurę, również od spodu, Dagmara pomalowała. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dokładnie 7 kostek ma pomalowane dokładnie 3 ściany. | P | F |
| Dokładnie 7 kostek ma pomalowane dokładnie 2 ściany. | P | F |
Trójkąt, w którym długości boków są do siebie w stosunku 3 : 4 : 5 nazywa się trójkątem egipskim. Z odcinków o jakich długościach nie można zbudować trójkąta egipskiego?
A) 6, 8, 10 B) 9, 12, 15 C) 12, 20, 25 D) 21, 28, 35
Do pudełka włożono 48 kul w różnych kolorach. Prawdopodobieństwo wylosowania kuli czerwonej jest równe  , a prawdopodobieństwo wylosowania kuli żółtej jest równe
, a prawdopodobieństwo wylosowania kuli żółtej jest równe 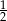 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pudełku jest trzy więcej kul czerwonych niż żółtych. | P | F |
| W pudełku może być 16 kul zielonych. | P | F |
W pięcioosobowej grupie średnia wieku trzech kobiet wynosi 26 lat, a średnia wieku dwóch mężczyzn 36 lat. Średnia wieku wszystkich osób jest równa
A) 33 lata B) 32 lata C) 31 lat D) 30 lat
W siedmioosobowej grupie średnia wieku trzech kobiet wynosi 29 lat, a średnia wieku czterech mężczyzn 36 lat. Średnia wieku wszystkich osób jest równa
A) 33 lata B) 32 lata C) 31 lata D) 30 lat
W dziewięcioosobowej grupie średnia wieku czterech kobiet wynosi 22 lata, a średnia wieku pięciu mężczyzn 40 lat. Średnia wieku wszystkich osób jest równa
A) 33 lata B) 32 lata C) 31 lata D) 30 lat
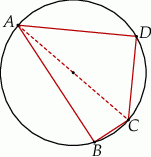
Czworokąt 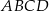 jest wpisany w okrąg, przy czym przekątna
jest wpisany w okrąg, przy czym przekątna 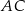 jest średnicą tego okręgu oraz
jest średnicą tego okręgu oraz 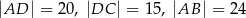 . Wtedy
. Wtedy
A) 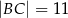 B)
B) 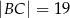 C)
C) 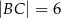 D)
D) 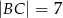
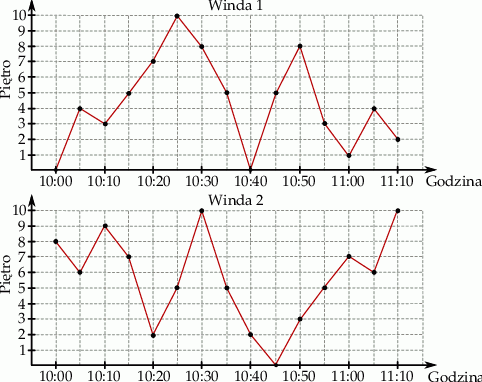
W budynku przeprowadzono test dwóch zainstalowanych w nim wind. W czasie procedury testowej każda z wind co 5 minut zatrzymywała się na jednym z pięter. Wykresy przedstawiają położenie każdej z wind w trakcie 70 minutowej procedury testowej.
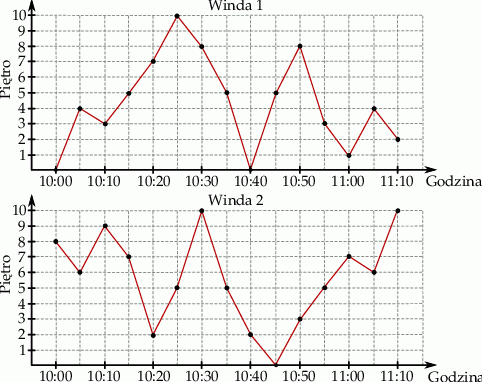
| W trakcie testu windy czterokrotnie znalazły się na tej samej wysokości. | P | F |
| Windy dwa razy zatrzymały się w tym samym czasie na tym samym piętrze. | P | F |
W budynku przeprowadzono test dwóch zainstalowanych w nim wind. W czasie procedury testowej każda z wind co 5 minut zatrzymywała się na jednym z pięter. Wykresy przedstawiają położenie każdej z wind w trakcie 70 minutowej procedury testowej.
Do dwóch koszy wrzucono piłki szare i czarne. Na diagramie przedstawiono liczbę piłek każdego koloru w I i w II koszu.
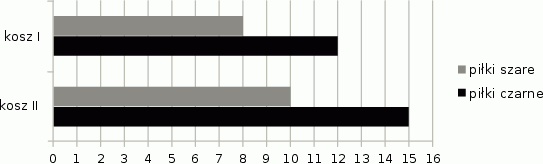
Czy wylosowanie piłki czarnej z kosza II jest bardziej prawdopodobne niż wylosowanie piłki czarnej z kosza I? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A. | w koszu II jest więcej piłek czarnych niż w koszu I. |
| B. | stosunek liczby piłek czarnych do liczby wszystkich piłek jest taki sam w obu koszach. |
| C. | w koszu II jest o 3 piłki czarne więcej niż w koszu I, ale szarych – tylko o 2 więcej. |
W pudełku są 2 kule zielone, 2 białe i 4 czarne. Losujemy z pudełka 1 kulę. Czy prawdziwe jest stwierdzenie, że prawdopodobieństwo wylosowania kuli czarnej jest dwa razy większe od prawdopodobieństwa wylosowania kuli białej? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w pudełku jest 2 razy mniej kul białych niż czarnych. |
| B) | w pudełku jest o połowę mniej kul zielonych niż kul czarnych. |
| C) | kule czarne stanowią połowę wszystkich kul w pudełku. |
W dwóch koszach umieszczono koszulki niebieskie i czerwone. Na diagramie przedstawiono liczbę koszulek każdego koloru w I i w II koszu.
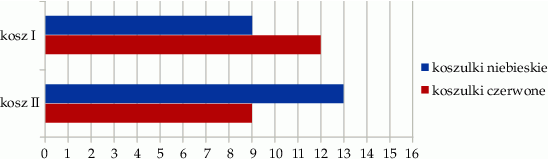
Czy wylosowanie niebieskiej koszulki z kosza I jest bardziej prawdopodobne niż wylosowanie czerwonej koszulki z kosza II? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w koszu I jest tyle samo koszulek niebieskich ile jest koszulek czerwonych w koszu II. |
| B) | stosunek liczby koszulek niebieskich do liczby koszulek czerwonych w I koszu jest taki sam jak stosunek liczby koszulek czerwonych do liczby koszulek niebieskich w II koszu. |
| C) | w koszu II jest więcej koszulek niebieskich niż jest koszulek czerwonych w pierwszym koszu. |
W pudełku są 2 kule zielone, 2 białe i 4 czarne. Losujemy z pudełka 1 kulę. Czy prawdziwe jest stwierdzenie, że prawdopodobieństwo wylosowania kuli czarnej jest równe 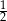 ? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w pudełku jest 2 razy mniej kul białych niż czarnych. |
| B) | w pudełku jest o połowę mniej kul zielonych niż kul czarnych. |
| C) | kule czarne stanowią połowę wszystkich kul w pudełku. |
Marża równa 1,5% kwoty pożyczonego kapitału była równa 3 000 zł. Wynika stąd, że pożyczono
A) 45 zł B) 2 000 zł C) 200 000 zł D) 450 000 zł
Marża równa 0,5% kwoty pożyczonego kapitału była równa 2 000 zł. Wynika stąd, że pożyczono
A) 4 000 zł B) 40 000 zł C) 200 000 zł D) 400 000 zł
W trójkącie równoramiennym o obwodzie 31 cm ramię jest dłuższe od podstawy o 5 cm. Ramię tego trójkąta ma długość
A) 24 cm B) 12 cm C) 7 cm D) 6 cm
Samolot pasażerski spala średnio 10 ton paliwa w ciągu godziny lotu.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W ciągu minuty lotu samolot spala ponad 200 kg paliwa. | P | F |
| Spalenie przez samolot 1800 kg paliwa trwa krócej niż 12 minut. | P | F |
Liczba 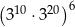 jest równa
jest równa
A) 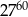 B)
B) 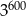 C)
C) 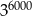 D)
D) 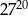
Liczba 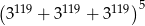 jest równa
jest równa
A) 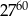 B)
B)  C)
C) 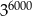 D)
D) 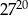
Trzecia część liczby 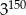 jest równa
jest równa
A) 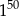 B)
B) 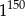 C)
C) 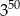 D)
D) 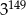
Trzecia część liczby 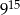 wynosi
wynosi
A) 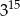 B)
B) 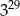 C)
C) 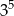 D)
D) 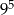
Szósta część liczby 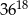 wynosi
wynosi
A) 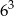 B)
B) 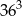 C)
C) 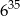 D)
D) 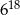
Trzecia część liczby 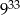 wynosi
wynosi
A) 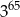 B)
B) 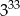 C)
C) 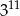 D)
D) 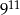
Połową liczby 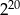 jest
jest
A) 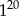 B)
B) 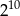 C)
C) 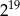 D)
D) 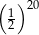
Połowa liczby 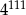 to
to
A) 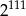 B)
B) 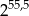 C)
C) 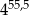 D)
D) 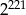
Połowa liczby 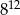 wynosi
wynosi
A) 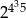 B)
B) 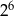 C)
C) 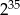 D)
D) 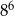
Połowa liczby 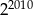 to
to
A) 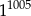 B)
B) 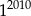 C)
C) 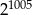 D)
D) 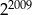
Liczba 9 razy mniejsza od 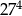 jest równa
jest równa
A) 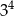 B)
B) 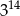 C)
C) 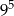 D)
D) 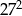
Liczba 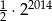 jest równa
jest równa
A) 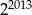 B)
B) 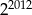 C)
C) 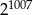 D)
D) 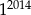
Trzecia część liczby 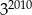 to
to
A) 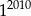 B)
B) 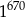 C)
C) 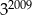 D)
D) 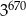
W trapezie 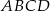 podstawa
podstawa 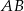 jest dłuższa od podstawy
jest dłuższa od podstawy 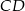 .
.
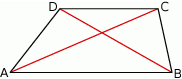
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 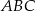 jest równe połowie pola trapezu jest równe połowie pola trapezu 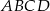 . . | P | F |
Suma pól trójkątów 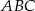 i i 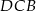 jest równa polu trapezu. jest równa polu trapezu. | P | F |
