Która z podanych niżej liczb nie jest równa 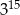 ?
?
A) 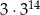 B)
B) 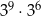 C)
C) 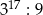 D)
D) 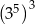 E)
E) 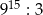
/Szkoła podstawowa/Zadania testowe
Która z podanych niżej liczb nie jest równa 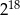 ?
?
A) 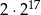 B)
B) 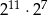 C)
C) 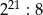 D)
D) 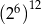 E)
E) 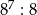
Korzystając z tego, że 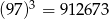 , wskaż wartość liczby
, wskaż wartość liczby 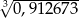 .
.
A) 0,0097 B) 0,097 C) 0,97 D) 9,7
W przedziale 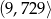 potęg liczby 3 jest
potęg liczby 3 jest
A) 6 B) 5 C) 4 D) 3
W przedziale 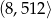 potęg liczby 2 jest
potęg liczby 2 jest
A) 6 B) 5 C) 4 D) 3
W przedziale 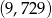 potęg liczby 3 jest
potęg liczby 3 jest
A) 6 B) 5 C) 4 D) 3
Na rysunku przedstawiono trzy figury: prostokąt, kwadrat, trójkąt.
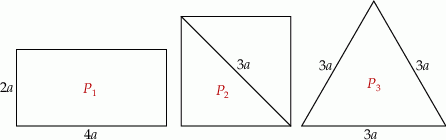
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Spośród przedstawionych figur największe pole ma figura  . . | P | F |
Spośród podanych figur najmniejsze pole ma figura  . . | P | F |
Siatka narysowanego graniastosłupa prostego składa się
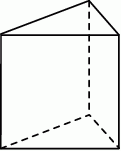
A) z 2 trójkątów i 2 prostokątów B) z 2 trójkątów i 3 prostokątów
C) z 3 trójkątów i 2 prostokątów D) z 3 trójkątów i 3 prostokątów
W konkursie przyznano nagrody pieniężne. Zdobywca pierwszego miejsca otrzymał 5000 zł. Nagroda za zdobycie drugiego miejsca była o 30% mniejsza niż nagroda za zajęcie pierwszego miejsca. Nagroda za zdobycie trzeciego miejsca była o 40% mniejsza niż nagroda za zajęcie drugiego miejsca. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Uczestnik konkursu, który zdobył trzecie miejsce, otrzymał 1400 zł. | P | F |
| Nagroda za zdobycie trzeciego miejsca była o 70% mniejsza od nagrody za zajęcie pierwszego miejsca. | P | F |
W konkursie przyznano nagrody pieniężne. Zdobywca trzeciego miejsca otrzymał 2500 zł. Nagroda za zdobycie drugiego miejsca była o 20% większa niż nagroda za zajęcie trzeciego miejsca. Nagroda za zdobycie pierwszego miejsca była o 40% większa niż nagroda za zajęcie drugiego miejsca. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Uczestnik konkursu, który zdobył pierwsze miejsce, otrzymał 4000 zł. | P | F |
| Nagroda za zdobycie pierwszego miejsca była o 68% większa od nagrody za zajęcie trzeciego miejsca. | P | F |
Ile jest liczb całkowitych, dla których wyrażenie 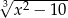 nie może być obliczone w zbiorze liczb rzeczywistych?
nie może być obliczone w zbiorze liczb rzeczywistych?
A) 0 B) 3 C) 6 D) 7
Jaki kąt tworzą wskazówki zegara o godzinie 9:00?
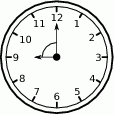
A) 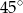 B)
B) 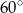 C)
C) 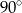 D)
D) 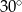
Liczbę 25520 można zapisać w postaci 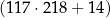 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Reszty z dzielenia liczby 25520 przez 117 i przez 109 są równe. | P | F |
| Reszta z dzielenia połowy liczby 25520 przez 117 jest równa 7. | P | F |
Jeżeli 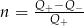 i
i 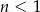 to
to
A) 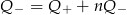 B)
B) 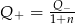 C)
C) 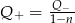 D)
D) 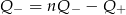
Jeżeli 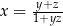 i
i 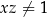 , to
, to
A) 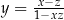 B)
B) 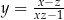 C)
C) 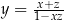 D)
D) 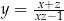
Suma sześciu kolejnych potęg naturalnych liczby 2 jest równa 2016. Najmniejszą z tych liczb jest
A) 5 B) 8 C) 16 D) 32
Ogrodnik kupił ziemię ogrodową, którą zaplanował zużyć w maju, czerwcu i lipcu. W maju zużył 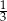 masy kupionej ziemi. W czerwcu zużył połowę masy ziemi, która została. Na lipiec pozostało mu jeszcze 60 kg ziemi. Jeżeli przez
masy kupionej ziemi. W czerwcu zużył połowę masy ziemi, która została. Na lipiec pozostało mu jeszcze 60 kg ziemi. Jeżeli przez  oznaczymy masę zakupionej ziemi, to sytuację przedstawioną w zadaniu opisuje równanie
oznaczymy masę zakupionej ziemi, to sytuację przedstawioną w zadaniu opisuje równanie
A) 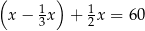 B)
B) 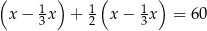
C) 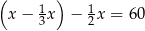 D)
D) 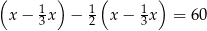
Ogrodnik kupił ziemię ogrodową, którą zaplanował zużyć w maju, czerwcu i lipcu. W maju zużył  masy kupionej ziemi. W czerwcu zużył
masy kupionej ziemi. W czerwcu zużył  masy ziemi, która została. Na lipiec pozostało mu jeszcze 50 kg ziemi. Jeżeli przez
masy ziemi, która została. Na lipiec pozostało mu jeszcze 50 kg ziemi. Jeżeli przez  oznaczymy masę zakupionej ziemi, to sytuację przedstawioną w zadaniu opisuje równanie
oznaczymy masę zakupionej ziemi, to sytuację przedstawioną w zadaniu opisuje równanie
A) 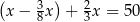 B)
B) 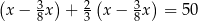
C) 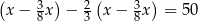 D)
D) 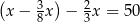
Do gry planszowej używane są dwa bączki o kształtach przedstawionych na rysunkach. Każdy bączek po zatrzymaniu na jednym boku wielokąta wskazuje liczbę umieszczoną na jego tarczy. Na rysunku I bączek ma kształt pięciokąta foremnego z zaznaczonymi liczbami od 1 do 5. Na rysunku II bączek ma kształt sześciokąta foremnego z zaznaczonymi liczbami od 1 do 6.
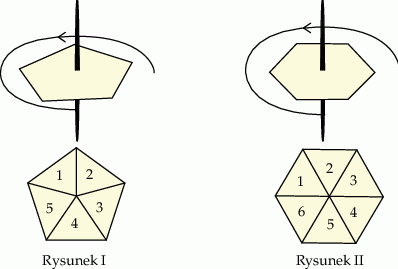
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo otrzymania liczby większej niż 3 na bączku z rysunku I jest większe niż 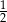 | P | F |
| Uzyskanie nieparzystej liczby na bączku z rysunku I jest tak samo prawdopodobne, jak uzyskanie nieparzystej liczby na bączku z rysunku II. | P | F |
Do gry planszowej używane są dwa bączki o kształtach przedstawionych na rysunkach. Każdy bączek po zatrzymaniu na jednym boku wielokąta wskazuje liczbę umieszczoną na jego tarczy. Na rysunku I bączek ma kształt siedmiokąta foremnego z zaznaczonymi liczbami od 1 do 7. Na rysunku II bączek ma kształt sześciokąta foremnego z zaznaczonymi liczbami od 1 do 6.
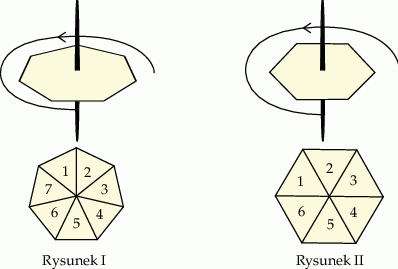
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo otrzymania liczby pierwszej na bączku z rysunku I jest większe niż 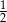 | P | F |
| Uzyskanie liczby parzystej na bączku z rysunku I jest tak samo prawdopodobne, jak uzyskanie liczby nieparzystej na bączku z rysunku II. | P | F |
Ania wycięła z kartki papieru dwa jednakowe trójkąty prostokątne o bokach długości 12 cm, 16 cm i 20 cm. Pierwszy z nich zagięła wzdłuż symetralnej krótszej przyprostokątnej, a drugi – wzdłuż symetralnej dłuższej przyprostokątnej. W ten sposób otrzymała czworokąty pokazane na rysunkach.
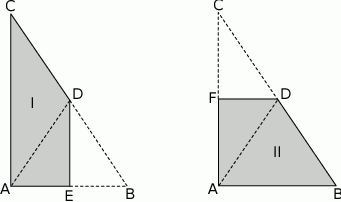
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pole czworokąta I jest równe polu czworokąta II. | P | F |
| Obwód czworokąta I jest mniejszy od obwodu czworokąta II. | P | F |
Jacek wyciął z kartki papieru dwa jednakowe trójkąty prostokątne o bokach długości 18 cm, 24 cm i 30 cm. Pierwszy z nich zagiął wzdłuż symetralnej dłuższej przyprostokątnej, a drugi – wzdłuż symetralnej krótszej przyprostokątnej. W ten sposób otrzymał czworokąty pokazane na rysunkach.
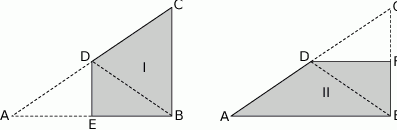
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pole czworokąta I jest równe polu czworokąta II. | P | F |
| Obwód czworokąta I jest mniejszy od obwodu czworokąta II. | P | F |
Dane są liczby 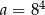 i
i 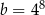 .
.
Aby otrzymać liczbę 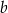 należy liczbę
należy liczbę  A/B.
A/B.
A) podnieść do kwadratu. B) pomnożyć przez 16.
Aby otrzymać liczbę 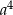 należy liczbę
należy liczbę 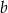 C/D.
C/D.
C) podnieść do potęgi 3. D) podnieść do potęgi 2.
Rowerzysta pokonuje trasę między miejscowościami  i
i  w ciągu 48 minut, a średnia prędkość piechura na tej samej trasie jest trzykrotnie mniejsza od średniej prędkości rowerzysty. O ile minut wcześniej niż rowerzysta piechur musi wyjść z miasta
w ciągu 48 minut, a średnia prędkość piechura na tej samej trasie jest trzykrotnie mniejsza od średniej prędkości rowerzysty. O ile minut wcześniej niż rowerzysta piechur musi wyjść z miasta  tak, aby obaj dotarli do miasta
tak, aby obaj dotarli do miasta  w tym samym momencie?
w tym samym momencie?
A) O 64 minuty. B) O 84 minut. C) O 96 minut. D) O 144 minuty.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| 120% liczby 180 to tyle samo, co 180% liczby 120. | P | F |
| 20% liczby 36 to tyle samo, co 40% liczby 18. | P | F |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| 40% liczby 140 to tyle samo, co 140% liczby 40. | P | F |
| 30% liczby 42 to tyle samo, co 60% liczby 84. | P | F |
Średnie zużycie paliwa na pierwszym odcinku trasy było równe 7 litrów na 100 kilometrów, a średnie zużycie paliwa na drugim, dwa razy dłuższym odcinku trasy, było równe 10 litrów na 100 kilometrów. Średnie zużycie paliwa na każde 100 km całej trasy wyniosło
A) 8 litrów. B) 8,5 litra. C) 7 litrów. D) 9 litrów.
W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera – spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 25% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe
A) 0,75 B) 0,25 C) 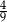 D)
D) 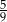
W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera – spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 40% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe
A) 0,6 B) 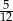 C)
C) 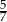 D) 0,4
D) 0,4
Na loterii stosunek liczby losów wygrywających do liczby losów przegrywających jest równy 2 : 7. Zakupiono jeden los z tej loterii. Prawdopodobieństwo zdarzenia polegającego na tym, że zakupiony los jest wygrywający, jest równe
A) 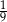 B)
B) 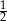 C)
C) 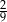 D)
D) 
Na loterii stosunek liczby losów wygrywających do liczby losów przegrywających jest równy 2 : 7. Zakupiono jeden los z tej loterii. Prawdopodobieństwo zdarzenia polegającego na tym, że zakupiony los jest przegrywający, jest równe
A) 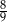 B)
B) 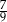 C)
C) 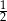 D)
D) 

