W trójkącie 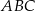 narysowano dwie wysokości:
narysowano dwie wysokości: 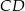 i
i 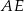 , jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy
, jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy 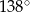 .
.
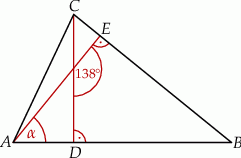
Jaką miarę ma kąt  zaznaczony na rysunku?
zaznaczony na rysunku?
A) 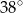 B)
B) 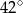 C)
C) 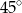 D)
D) 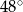
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 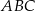 narysowano dwie wysokości:
narysowano dwie wysokości: 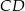 i
i 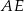 , jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy
, jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy 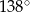 .
.

Jaką miarę ma kąt  zaznaczony na rysunku?
zaznaczony na rysunku?
A) 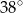 B)
B) 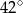 C)
C) 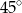 D)
D) 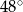
W trójkącie 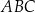 narysowano dwie wysokości:
narysowano dwie wysokości: 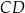 i
i 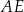 , jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy
, jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy 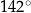 .
.
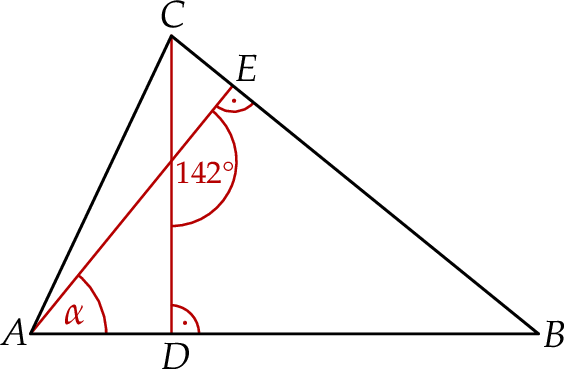
Jaką miarę ma kąt  zaznaczony na rysunku?
zaznaczony na rysunku?
A) 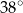 B)
B) 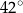 C)
C) 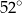 D)
D) 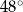
Na rysunku przedstawiono schemat budowy muru z cegieł oraz dwa przykładowe mury: jeden o szerokości 5 i wysokości 3 cegieł oraz drugi o szerokości 6 i wysokości 5 cegieł.

Do zbudowania muru o szerokości  i wysokości 11 cegieł potrzeba
i wysokości 11 cegieł potrzeba
A) 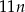 cegieł. B)
cegieł. B) 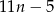 cegieł. C)
cegieł. C) 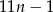 cegieł. D)
cegieł. D) 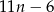 cegieł.
cegieł.
Na rysunku przedstawiono schemat budowy muru z cegieł oraz dwa przykładowe mury: jeden o szerokości 5 i wysokości 3 cegieł oraz drugi o szerokości 6 i wysokości 5 cegieł.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli zwiększamy szerokość muru dwukrotnie, to liczba cegieł potrzebnych do jego budowy również rośnie dwukrotnie. | P | F |
| W każdym ze zbudowanych w ten sposób murów liczba cegieł jest liczbą parzystą. | P | F |
Okrąg wpisany w czworokąt 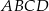 ma środek
ma środek 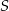 i jest styczny do boków
i jest styczny do boków 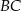 i
i 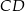 odpowiednio w punktach
odpowiednio w punktach 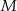 i
i 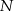 . Kąt
. Kąt 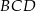 ma miarę
ma miarę 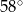 (rysunek).
(rysunek).
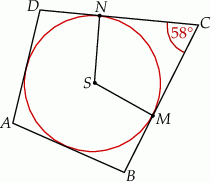
Kąt 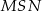 ma miarę
ma miarę
A) 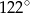 B)
B) 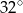 C)
C) 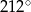 D)
D) 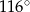
Wierzchołek 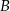 równoległoboku
równoległoboku 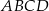 ma współrzędne
ma współrzędne
A) 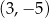 B)
B) 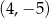 C)
C) 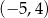 D)
D) 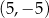
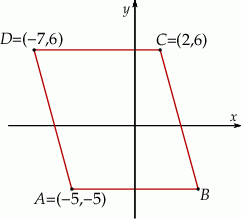
Na rysunku przedstawiono równoległobok 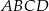
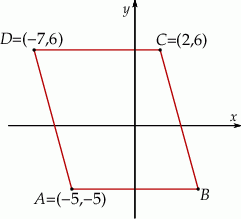
Pole równoległoboku 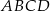 jest równe A/B.
jest równe A/B.
A) 99 B) 80
Wierzchołek 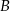 równoległoboku
równoległoboku 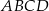 ma współrzędne C/D.
ma współrzędne C/D.
C) 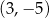 D)
D) 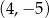
Asia jeździła rowerem 2 godziny. Na diagramie przedstawiono w procentach (w %) czas jazdy Asi po leśnej drodze, ścieżce rowerowej i polnej drodze, ale nie narysowano słupka z informacją o czasie jazdy po chodniku.
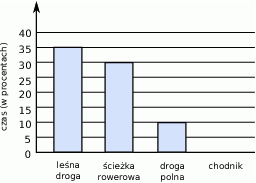
Asia jeździła rowerem 2 godziny. Na diagramie przedstawiono w procentach (w %) czas jazdy Asi po leśnej drodze, ścieżce rowerowej i polnej drodze, ale nie narysowano słupka z informacją o czasie jazdy po chodniku.
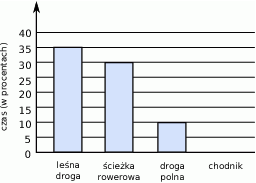
Na giełdzie kupiono tę samą liczbę akcji dwóch przedsiębiorstw, przy czym średnia cena zakupu jednej akcji drugiego przedsiębiorstwa była dwa razy wyższa od średniej ceny akcji pierwszego przedsiębiorstwa. Ile średnio zapłacono za jedną akcję drugiego przedsiębiorstwa, jeżeli średnia cena zakupu wszystkich akcji wyniosła 90 zł?
A) 30 zł B) 60 zł C) 90 zł D) 120 zł
Właściciel salonu samochodowego sporządził diagram, na którym zaznaczył miesięczną sprzedaż samochodów w okresie styczeń 2017 – grudzień 2018.
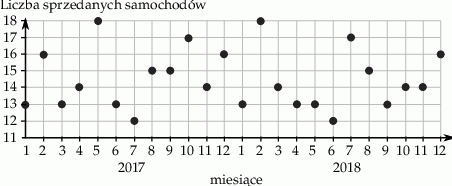
W którym z podanych okresów sprzedano najmniejszą liczbę samochodów?
A) styczeń 2017 – czerwiec 2017 B) lipiec 2017 – grudzień 2017
C) styczeń 2018 – czerwiec 2018 D) lipiec 2018 – grudzień 2018
Właściciel salonu samochodowego sporządził diagram, na którym zaznaczył miesięczną sprzedaż samochodów w okresie styczeń 2017 – grudzień 2018.
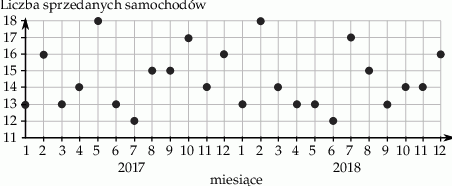
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Łączna sprzedaż samochodów w dwóch kolejnych miesiącach nigdy nie przekroczyła 32 sztuk. | P | F |
| Liczba miesięcy, w których sprzedaż przekroczyła 15 samochodów była większa niż liczba miesięcy, w których sprzedaż była mniejsza niż 15 samochodów. | P | F |
Z reguł działań na potęgach wynika, że:
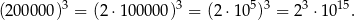
Z tych samych reguł wynika, że liczba 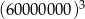 jest równa
jest równa
A) 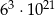 B)
B) 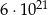 C)
C) 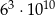 D)
D) 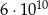
Z reguł działań na potęgach wynika, że:
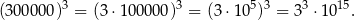
Z tych samych reguł wynika, że liczba 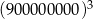 jest równa
jest równa
A) 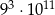 B)
B) 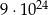 C)
C) 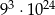 D)
D) 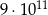
Wiadomo, że mediana liczb 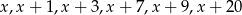 jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 5 B) 26 C) 28 D) 4
Wiadomo, że mediana liczb 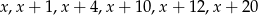 jest równa 11. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 11. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 4 B) 28 C) 22 D) 24
Wiadomo, że mediana liczb 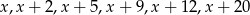 jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 2 B) 16 C) 22 D) 24
Poniżej przedstawiono składniki potrzebne do przygotowania ciasta na 8 gofrów.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Do przygotowania ciasta na 40 gofrów, przy zachowaniu właściwych proporcji odpowiednich składników, potrzeba 10 jajek. | P | F |
| Do przygotowania ciasta na 72 gofry, przy zachowaniu właściwych proporcji odpowiednich składników, potrzeba 12 szklanek mleka. | P | F |
Poniżej przedstawiono składniki potrzebne do przygotowania ciasta na 15 racuchów.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Do przygotowania ciasta na 40 racuchów, przy zachowaniu właściwych proporcji odpowiednich składników, potrzeba 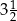 szklanki mąki. szklanki mąki. | P | F |
Do przygotowania ciasta na 54 racuchy, przy zachowaniu właściwych proporcji odpowiednich składników, potrzeba 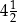 szklanki mleka. szklanki mleka. | P | F |
Poniżej przedstawiono listę produktów, z których przygotowano 8 identycznych paczek świątecznych.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Do przygotowania kolejnych 17 paczek świątecznych, o takiej samej zawartości jak pierwsze 8 paczek, potrzeba ponad 6 kg suszonych owoców. | P | F |
| Gdyby przygotować 73 paczki świąteczne, o takiej samej zawartości jak 8 paczek opisanych w treści zadania, to w tych 73 paczkach liczba pierniczków byłaby równa sumie liczby mandarynek i liczby lizaków. | P | F |
Jeżeli trzecia część liczby przeciwnej do odwrotności sześcianu pewnej liczby jest równa 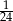 , to ta liczba jest równa
, to ta liczba jest równa
A) 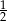 B) 2 C)
B) 2 C) 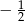 D)
D) 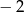
Dane są trzy wyrażenia:
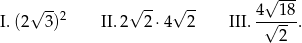
Wartości których wyrażeń są mniejsze od 15?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) I, II i III.
Dane są trzy wyrażenia:
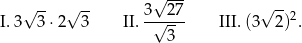
Wartości których wyrażeń są większe od 6?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) I, II i III.
Dany jest trójkąt 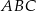 , w którym kąt
, w którym kąt 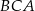 ma miarę
ma miarę 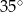 . Punkt
. Punkt 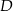 leży na boku
leży na boku 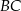 tego trójkąta. Odcinek
tego trójkąta. Odcinek 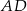 ma taką samą długość jak odcinek
ma taką samą długość jak odcinek 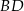 . Kąt
. Kąt 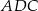 ma miarę
ma miarę 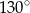 (zobacz rysunek poniżej).
(zobacz rysunek poniżej).
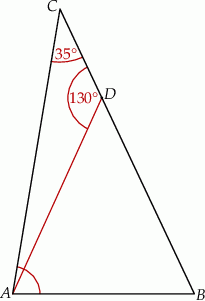
Kąt 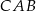 ma miarę
ma miarę
A) 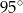 B)
B) 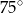 C)
C) 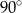 D)
D) 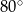
Dany jest trójkąt 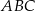 , w którym kąt
, w którym kąt 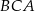 ma miarę
ma miarę 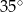 . Punkt
. Punkt 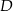 leży na boku
leży na boku 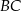 tego trójkąta. Odcinek
tego trójkąta. Odcinek 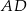 ma taką samą długość jak odcinek
ma taką samą długość jak odcinek 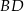 . Kąt
. Kąt 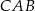 ma miarę
ma miarę 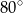 (zobacz rysunek poniżej).
(zobacz rysunek poniżej).
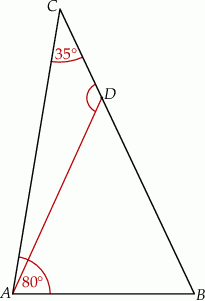
Kąt 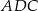 ma miarę
ma miarę
A) 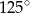 B)
B) 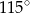 C)
C) 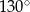 D)
D) 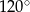
Narysowana poniżej figura składa się z kwadratu o boku 2 i trzech ćwiartek koła.
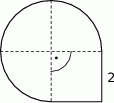
Obwód tej figury jest równy
A) 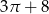 B)
B) 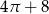 C)
C) 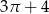 D)
D) 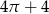
Narysowana poniżej figura składa się z dwóch kwadratów o boku 2 i dwóch ćwiartek koła.
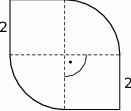
Obwód tej figury jest równy
A) 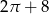 B)
B) 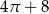 C)
C) 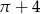 D)
D) 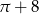
Z kartki w kształcie kwadratu o boku 6 odcięto ćwierć koła o promieniu 6 (patrz rysunek).
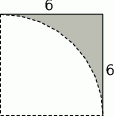
Pole powierzchni pozostałej zacieniowanej części kartki jest równe
A) 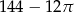 B)
B) 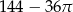 C)
C) 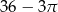 D)
D) 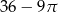
Na rysunku przedstawiono trapez równoramienny o podstawach 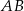 i
i 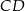 . Dane są długości odcinków
. Dane są długości odcinków 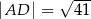 ,
, 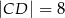 ,
, 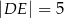 .
.
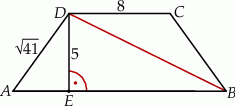
Długość przekątnej 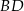 jest równa
jest równa
A) 13 B) 14 C) 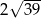 D)
D) 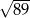
Dane są liczby: 12195, 43176, 54145, 57492, 61020, 37170.
Wśród danych liczb są dokładnie A/B liczby podzielne przez 12.
A) trzy B) cztery
Wśród danych liczb są dokładnie C/D liczby podzielne przez 45.
C) dwie D) trzy
Dwa sześciany – jeden o krawędzi 2 i drugi o krawędzi 3 – pocięto na sześciany o krawędzi 1. Z otrzymanych sześcianów zbudowano prostopadłościan. Żadna ściana tego prostopadłościanu nie jest kwadratem. Pole powierzchni zbudowanego prostopadłościanu jest równe
A) 35 B) 47 C) 94 D) 142
Dwa sześciany – jeden o krawędzi 3 i drugi o krawędzi 4 – pocięto na sześciany o krawędzi 1. Z otrzymanych sześcianów zbudowano prostopadłościan. Żadna ściana tego prostopadłościanu nie jest kwadratem. Pole powierzchni zbudowanego prostopadłościanu jest równe
A) 150 B) 222 C) 366 D) 111
W prostokątnym układzie współrzędnych przedstawiono wykres funkcji.
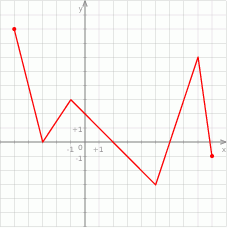
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 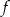 dla argumentów ujemnych przyjmuje wartości dodatnie. dla argumentów ujemnych przyjmuje wartości dodatnie. | P | F |
Funkcja 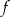 pewną wartość przyjmuje dla 4 argumentów. pewną wartość przyjmuje dla 4 argumentów. | P | F |
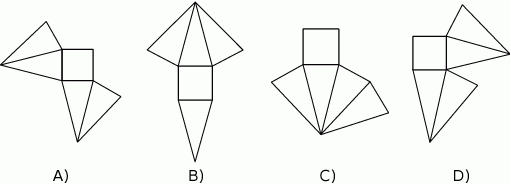
Który z poniższych rysunków nie może być siatką ostrosłupa prawidłowego czworokątnego?
Liczba 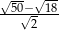 jest równa
jest równa
A) 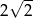 B) 2 C) 4 D)
B) 2 C) 4 D) 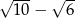
Liczba 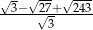 jest równa
jest równa
A) 5 B) 6 C) 7 D) 8
Iloraz 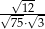 jest równy
jest równy
A) 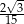 B)
B)  C)
C) 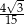 D)
D) 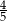
Liczba 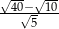 jest równa
jest równa
A) 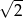 B)
B) 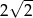 C) 4 D)
C) 4 D) 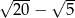
Iloraz 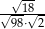 jest równy
jest równy
A)  B)
B) 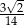 C)
C) 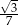 D)
D) 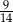
Liczba 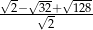 jest równa
jest równa
A) 7 B) 6 C) 5 D) 4
