Liczbę 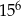 można zapisać jako
można zapisać jako
A) 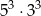 B)
B) 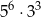 C)
C) 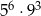 D)
D) 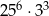
/Szkoła podstawowa/Zadania testowe
Połową odwrotności sześcianu liczby 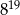 jest
jest
A) 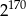 B)
B) 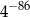 C)
C) 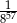 D)
D) 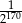
Połową odwrotności sześcianu liczby 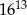 jest
jest
A) 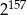 B)
B) 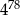 C)
C) 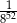 D)
D) 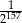
Połową odwrotności sześcianu liczby 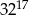 jest
jest
A) 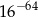 B)
B) 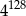 C)
C) 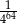 D)
D) 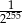
Ola przygotowując się do egzaminu rozwiązywała zadania z matematyki. Wykres przedstawia liczbę rozwiązanych zadań w zależności od czasu.
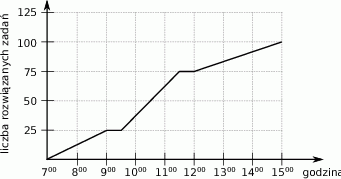
Na podstawie wykresu wybierz zdanie fałszywe.
A) O godzinie
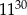 Ola rozpoczęła przerwę.
Ola rozpoczęła przerwę. B) Od
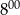 do
do 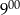 Ola rozwiązała mniej zadań niż od
Ola rozwiązała mniej zadań niż od 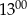 do
do 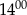 .
. C) Od
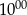 do
do 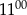 Ola rozwiązywała zadania w tempie 25 zadań na godzinę.
Ola rozwiązywała zadania w tempie 25 zadań na godzinę. D) Przez ostatnie trzy godziny Ola rozwiązała 25 zadań.
Ola przygotowując się do egzaminu rozwiązywała zadania z matematyki. Wykres przedstawia liczbę rozwiązanych zadań w zależności od czasu.
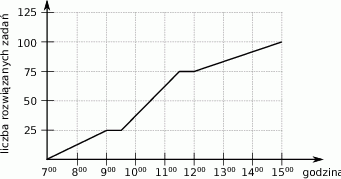
Kolejnego dnia Ola ponownie rozwiązywała zadania, ale poświęciła na to 6 godzin. Okazało się jednak, że średnie tempo rozwiązywania zadań było identyczne, jak w dniu przedstawionym na wykresie. Ile zadań Ola rozwiązała drugiego dania nauki?
A) 75 B) 80 C) 90 D) 60
Grupa młodzieży wybrała się na spacer po lesie. W trakcie wycieczki dwukrotnie zrobiono przerwę na odpoczynek. Wykres przedstawia zależność przebytej drogi od czasu trwania spaceru.
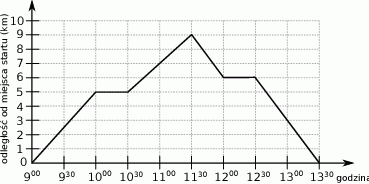
Które z poniższych zdań jest fałszywe?
A) Czas poświęcony na przerwy stanowił ponad 20% czasu całej wycieczki.
B) W trakcie wycieczki młodzież pokonała dystans 9 kilometrów.
C) W ciągu ostatniej godziny młodzież pokonała 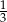 całej trasy.
całej trasy.
D) Pomiędzy przerwami młodzież pokonała dystans 7 kilometrów.
Grupa młodzieży wybrała się na spacer po lesie. W trakcie wycieczki dwukrotnie zrobiono przerwę na odpoczynek. Wykres przedstawia zależność przebytej drogi od czasu trwania spaceru.
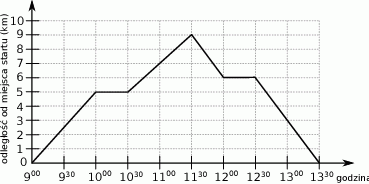
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Bezpośrednio przed drugą przerwą prędkość poruszania się grupy była taka sama jak tuż przed zakończeniem wycieczki. | P | F |
| W czasie pomiędzy przerwami grupa poruszała się ze stałą prędkością. | P | F |
Na osi liczbowej dane są liczby  i
i 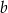
![]()
Liczby  i
i 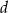 są zaokrągleniami odpowiednio liczb
są zaokrągleniami odpowiednio liczb  i
i 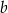 do części setnych. Suma
do części setnych. Suma  jest równa:
jest równa:
A) 0,22 B) 0,14 C) 0,07 D) 0,08
Ania z patyczków jednakowej długości buduje różne trójkąty

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Ania z 86 takich patyczków może zbudować trójkąt równoboczny | P | F |
| Ania z 48 takich patyczków może zbudować trójkąt prostokątny. | P | F |
Rozmiary kół rowerowych podaje się zwykle w calach. Średnica obręczy pewnego koła jest równa 22 cale.
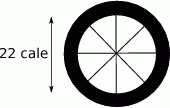
Ile centymetrów ma promień obręczy tego koła, jeśli 1 cal = 2,54 cm?
A) 22 cm B) 27,94 cm C) 11 cm D) 8,66 cm
Liczba 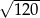 znajduje się na osi liczbowej między
znajduje się na osi liczbowej między
A) 10 i 11 B) 11 i 12 C) 12 i 20 D) 30 i 40
Liczba 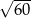 jest
jest
A) większa od 3 i mniejsza od 4. B) większa od 4 i mniejsza od 5.
C) większa od 7 i mniejsza od 8. D) większa od 8 i mniejsza od 9.
Liczba 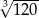 znajduje się na osi liczbowej między
znajduje się na osi liczbowej między
A) 10 i 11 B) 5 i 6 C) 4 i 5 D) 6 i 7
Liczba 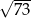 jest
jest
A) większa od 3 i mniejsza od 4. B) większa od 4 i mniejsza od 5.
C) większa od 7 i mniejsza od 8. D) większa od 8 i mniejsza od 9.
Liczba 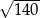 znajduje się na osi liczbowej między
znajduje się na osi liczbowej między
A) 10 i 11 B) 11 i 12 C) 12 i 20 D) 30 i 40
Drewnianą kostkę sześcienną o krawędzi długości 30 cm rozcięto na 27 jednakowych mniejszych sześciennych kostek. Z ośmiu takich małych kostek ułożono nowy sześcian.
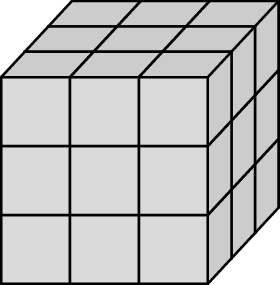
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole powierzchni nowego sześcianu jest równe 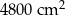 . . | P | F |
Objętość nowego sześcianu jest równa 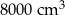 . . | P | F |
Dane jest wyrażenie
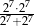
Czy wartość tego wyrażenia jest liczbą podzielną przez 8? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | każdy z wykładników jest liczbą nieparzystą. |
| B) | wykładnik potęgi 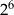 nie jest podzielny przez 8. nie jest podzielny przez 8. |
| C) | wartość tego wyrażenia można zapisać w postaci 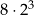 . . |
Przekątne trapezu 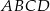 przedstawionego na rysunku przecinają się w punkcie
przedstawionego na rysunku przecinają się w punkcie 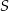 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt  ma miarę ma miarę  . . | P | F |
Trójkąty 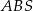 i i 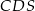 mają równe kąty. mają równe kąty. | P | F |
Na boku 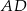 kwadratu
kwadratu 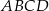 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 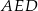 . Punkt
. Punkt 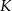 jest środkiem odcinka
jest środkiem odcinka 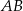 , a punkt
, a punkt 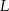 środkiem odcinka
środkiem odcinka 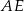 .
.
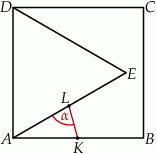
Miara kąta  jest równa
jest równa
A) 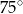 B)
B) 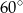 C)
C) 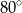 D)
D) 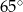
Czy 18% liczby 15 jest większe niż 15% liczby 18? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | 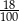 to więcej niż to więcej niż 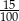 . . |
| B) | 1% liczby 15 to mniej niż 1% liczby 18. |
| C) | 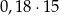 to tyle samo, ile to tyle samo, ile 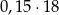 . . |
Piłki tenisowe zapakowano do 186 jednakowych pudełek. Do każdego z tych pudełek włożono po 6 piłek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba wszystkich spakowanych piłek jest podzielna przez 4. | P | F |
| Wszystkie te piłki można byłoby spakować do większych pudełek – po 9 piłek w każdym. | P | F |
Batony czekoladowe zapakowano do 492 jednakowych pudełek. Do każdego z tych pudełek włożono po 12 batonów. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba wszystkich spakowanych batonów jest podzielna przez 48. | P | F |
| Wszystkie te batony można byłoby spakować do większych pudełek – po 32 batony w każdym. | P | F |
Zbiornik w kształcie odwróconego stożka jest napełniany wodą przy pomocy pompy pracującej ze stałą wydajnością. Napełnienie zbiornika do 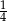 wysokości trwa 15 minut.
wysokości trwa 15 minut.
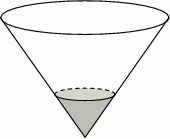
Oceń prawdziwość podanych zdań.
| Napełnienie całego zbiornika trwa 16 godzin. | P | F |
| Napełnienie zbiornika do połowy wysokości trwa 30 minut. | P | F |
Jaki jest wzór funkcji przedstawionej na wykresie?
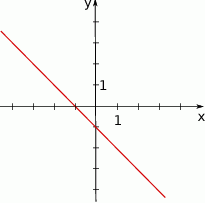
A) 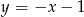 B)
B) 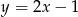 C)
C) 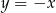 D)
D) 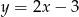
Jaki jest wzór funkcji przedstawionej na wykresie?
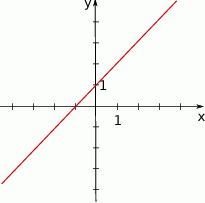
A) 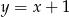 B)
B) 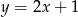 C)
C) 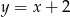 D)
D) 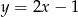
Jaki jest wzór funkcji przedstawionej na wykresie?
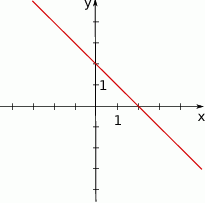
A) 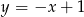 B)
B) 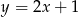 C)
C) 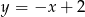 D)
D) 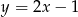
Na rysunku przedstawiono dwa trójkąty prostokątne.
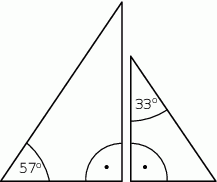
Czy te trójkąty są trójkątami podobnymi? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród zdań oznaczonych literami A–C.
| Tak | Nie |
| ponieważ | |
| A) | każde dwa trójkąty prostokątne są podobne. |
| B) | miary kątów ostrych jednego trójkąta są różne od miar kątów ostrych drugiego trójkąta. |
| C) | miary kątów ostrych jednego trójkąta są takie same jak miary kątów ostrych drugiego trójkąta. |
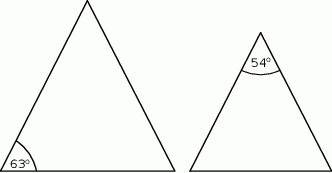
Na rysunku przedstawiono dwa trójkąty prostokątne.
Czy te trójkąty są trójkątami podobnymi? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród zdań oznaczonych literami A–C.
| Tak | Nie |
| ponieważ | |
| A) | każde dwa trójkąty prostokątne są podobne. |
| B) | miary kątów ostrych jednego trójkąta są różne od miar kątów ostrych drugiego trójkąta. |
| C) | miary kątów ostrych jednego trójkąta są takie same jak miary kątów ostrych drugiego trójkąta. |
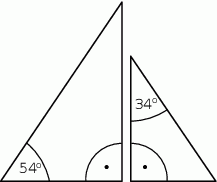
Na rysunku przedstawiono dwa trójkąty równoramienne.
Czy te trójkąty są trójkątami podobnymi? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród zdań oznaczonych literami A–C.
| Tak | Nie |
| ponieważ | |
| A) | każde dwa trójkąty równoramienne są podobne. |
| B) | miary kątów jednego trójkąta są różne od miar kątów drugiego trójkąta. |
| C) | miary kątów jednego trójkąta są takie same jak miary kątów drugiego trójkąta. |
| D) | długości ramion jednego trójkąta są różne od długości ramion drugiego trójkąta. |
Na rysunku przedstawiono dwa prostokąty.

Czy te prostokąty te są figurami podobnymi? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród zdań oznaczonych literami A–C.
| Tak | Nie |
| ponieważ | |
| A) | każde dwa prostokąty są podobne. |
| B) | długości boków jednego prostokąta nie są proporcjonalne do długości boków drugiego prostokąta. |
| C) | długości boków jednego prostokąta są proporcjonalne do długości boków drugiego prostokąta. |
Ile jest liczb naturalnych  takich, że największy dzielnik liczby
takich, że największy dzielnik liczby  , który jest od niej mniejszy to 5?
, który jest od niej mniejszy to 5?
A) 2 B) 4 C) 6 D) 3
Na diagramie przedstawiono wyniki ankiety, w której uczniowie pewnej szkoły odpowiadali na pytanie „Jakie jest twoje ulubione zwierzę domowe?”. Każdy ankietowany uczeń podawał tylko jedno zwierzę. Chomik był ulubieńcem 16 uczniów.
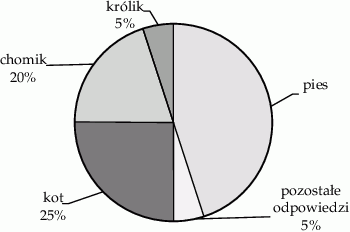
Które z podanych zdań jest fałszywe?
A) Pies był ulubieńcem 45% uczniów biorących udział w ankiecie.
B) Królika wskazało 4 razy mniej uczniów niż chomika.
C) Kota wskazało 24 ankietowanych uczniów.
D) W ankiecie wzięło udział 80 uczniów.
Na diagramie przedstawiono wyniki ankiety, w której działkowcy odpowiadali na pytanie „Jakiego ptaka najczęściej widują na swojej działce?”. Każdy ankietowany działkowiec podawał tylko jeden gatunek ptaka. Sikorkę wskazało 9 działkowców.
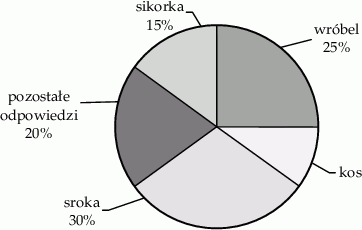
Które z podanych zdań jest fałszywe?
A) Sikorkę wskazało 2 razy mniej działkowców niż srokę.
B) Kosa wskazało 10% ankietowanych działkowców.
C) Kosa wskazało 6 ankietowanych działkowców.
D) W ankiecie wzięło udział 80 działkowców.
W każdym z dwóch pudełek są tylko kule białe i czarne. Prawdopodobieństwo wylosowania kuli czarnej z pierwszego pudełka jest równe 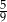 . W drugim pudełku jest dwa razy więcej kul białych i trzy razy więcej kul czarnych niż w pierwszym pudełku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. W drugim pudełku jest dwa razy więcej kul białych i trzy razy więcej kul czarnych niż w pierwszym pudełku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pierwszym pudełku są 4 kule białe. | P | F |
Prawdopodobieństwo wylosowania kuli białej z drugiego pudełka jest równe 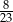 . . | P | F |

