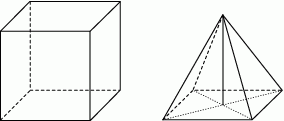
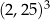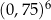Na rysunku przedstawiono ostrosłup prawidłowy czworokątny i sześcian. Bryły mają jednakowe podstawy i równe wysokości, a suma objętości tych brył jest równa 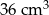 .
.
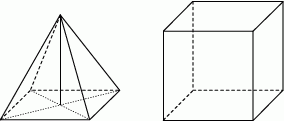
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Objętość sześcianu jest trzy razy większa od objętości ostrosłupa. | P | F |
| Krawędź sześcianu ma długość 3 cm. | P | F |

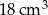 .
. 
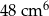 .
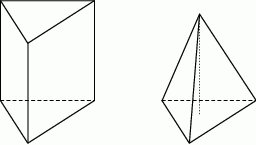
. 
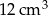 .
. 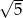 . Bok kwadratu jest równy
. Bok kwadratu jest równy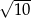
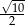
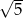
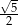
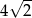
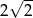
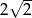
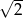
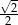
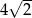
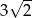
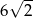
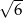 . Bok kwadratu jest równy
. Bok kwadratu jest równy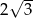
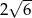
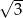
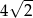
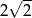
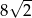
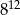 jest równa
jest równa 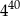
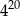
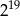
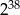
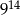 jest równa
jest równa 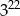
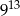
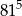
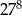
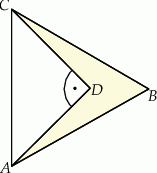
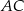 trójkąt równobocznego
trójkąt równobocznego 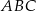 o polu równym
o polu równym 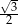 zbudowano równoramienny trójkąt prostokątny
zbudowano równoramienny trójkąt prostokątny 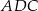 .
. 
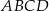 jest równe
jest równe 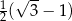 .
. jest równy
jest równy 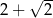 .
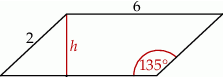
.
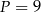
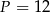
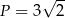
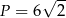
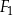 , kwadrat
, kwadrat 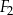 i prostokąt
i prostokąt 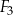 , oraz podano ich wymiary.
, oraz podano ich wymiary. 
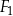 ,
, 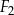 ,
, 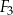 można ułożyć, bez rozcinania tych figur, kwadrat
można ułożyć, bez rozcinania tych figur, kwadrat 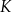 o polu
o polu 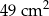 ? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C. 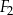 i
i 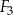 jest równa obwodowi kwadratu
jest równa obwodowi kwadratu 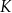 .
. 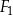 ,
, 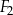 i
i 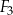 jest równa
jest równa 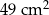 .
. 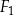 ,
, 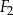 i
i 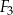 nie jest równa 7 cm.
nie jest równa 7 cm. 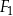 , prostokąt
, prostokąt 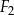 i prostokąt
i prostokąt 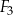 , oraz podano ich wymiary.
, oraz podano ich wymiary. 
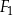 ,
, 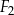 ,
, 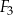 można ułożyć, bez rozcinania tych figur, kwadrat
można ułożyć, bez rozcinania tych figur, kwadrat 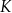 o obwodzie 28 cm? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
o obwodzie 28 cm? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C. 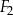 i
i 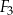 jest równa obwodowi kwadratu
jest równa obwodowi kwadratu 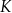 .
. 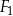 ,
, 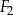 i
i 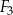 nie jest równa
nie jest równa 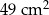 .
. 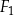 ,
, 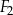 i
i  nie jest równa 7 cm.
nie jest równa 7 cm. 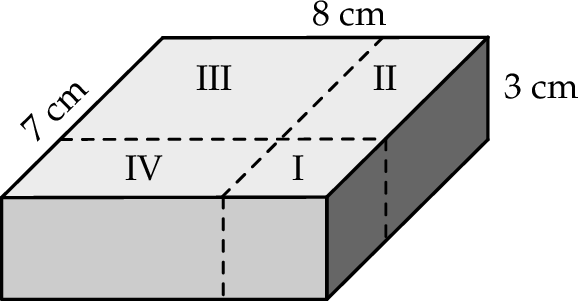
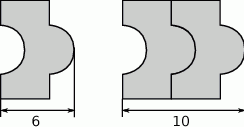
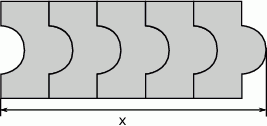
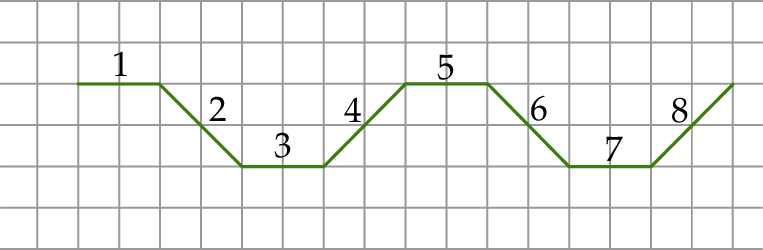
 ma długość
ma długość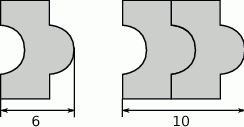
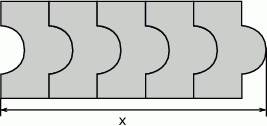
 odcinka dla wzoru złożonego z
odcinka dla wzoru złożonego z  płytek?
płytek? 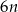
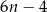
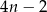
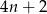
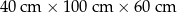 . Jeżeli każdą z najdłuższych krawędzi tego prostopadłościanu wydłużymy o 30%, a każdą z najkrótszych krawędzi skrócimy o 20%, to w wyniku obu tych przekształceń objętość tego prostopadłościanu
. Jeżeli każdą z najdłuższych krawędzi tego prostopadłościanu wydłużymy o 30%, a każdą z najkrótszych krawędzi skrócimy o 20%, to w wyniku obu tych przekształceń objętość tego prostopadłościanu 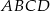 połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat 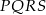 .
. 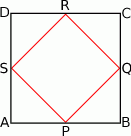
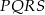 jest podobny do kwadratu
jest podobny do kwadratu 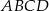 w skali
w skali 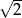
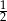
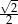
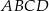 połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat 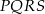 .
. 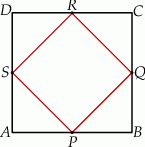
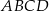 jest podobny do kwadratu
jest podobny do kwadratu 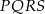 w skali
w skali 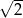
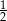
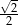
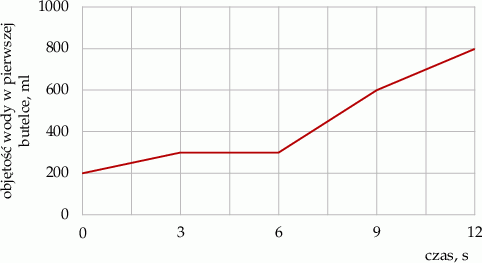
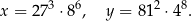
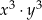 jest równy A/B.
jest równy A/B.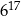
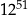
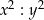 jest równy C/D.
jest równy C/D.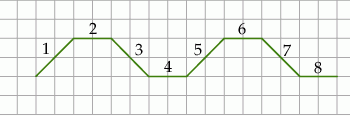
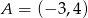 jest początkiem odcinka
jest początkiem odcinka 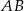 , gdzie
, gdzie 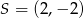 jest jego środkiem. Punkt
jest jego środkiem. Punkt 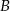 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne 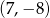
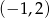
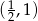
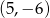
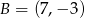 jest końcem odcinka
jest końcem odcinka 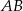 , gdzie
, gdzie 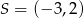 jest jego środkiem. Punkt
jest jego środkiem. Punkt 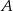 , który jest początkiem tego odcinka ma współrzędne
, który jest początkiem tego odcinka ma współrzędne 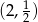
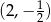
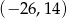
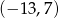
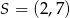 jest środkiem odcinka
jest środkiem odcinka 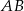 , w którym
, w którym 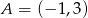 . Punkt
. Punkt 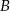 ma współrzędne:
ma współrzędne: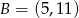
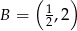
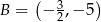
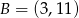
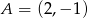 jest początkiem odcinka
jest początkiem odcinka 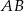 , gdzie
, gdzie 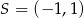 jest jego środkiem. Punkt
jest jego środkiem. Punkt 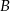 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne 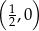
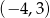
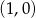
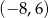
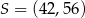 jest środkiem odcinka
jest środkiem odcinka 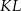 , którego jednym z końców jest punkt
, którego jednym z końców jest punkt 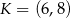 . Zatem
. Zatem 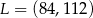
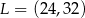
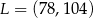
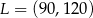
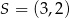 jest środkiem odcinka
jest środkiem odcinka 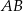 , w którym
, w którym 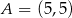 . Punkt
. Punkt 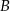 ma współrzędne
ma współrzędne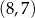
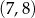
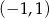
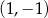
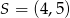 jest środkiem odcinka
jest środkiem odcinka 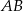 , w którym
, w którym 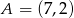 . Punkt
. Punkt 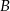 ma współrzędne:
ma współrzędne: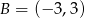
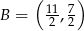
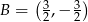
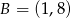
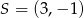 jest środkiem odcinka
jest środkiem odcinka 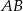 i
i 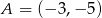 . Punkt
. Punkt 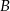 ma współrzędne
ma współrzędne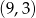
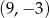
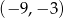
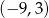
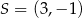 jest środkiem odcinka
jest środkiem odcinka 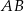 , w którym
, w którym 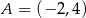 . Punkt
. Punkt 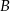 ma współrzędne
ma współrzędne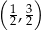
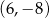
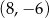
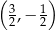
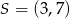 jest środkiem odcinka
jest środkiem odcinka 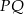 , gdzie
, gdzie 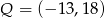 . Zatem punkt
. Zatem punkt 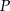 ma współrzędne
ma współrzędne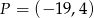
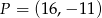
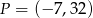
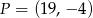
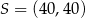 jest środkiem odcinka
jest środkiem odcinka 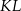 , którego jednym z końców jest punkt
, którego jednym z końców jest punkt 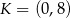 . Zatem
. Zatem 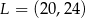
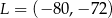
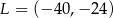
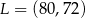
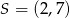 jest środkiem odcinka
jest środkiem odcinka 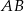 , w którym
, w którym 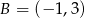 . Punkt
. Punkt 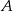 ma współrzędne:
ma współrzędne: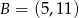
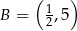
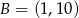
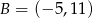
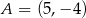 i
i 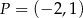 . Punkt
. Punkt 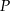 jest środkiem odcinka
jest środkiem odcinka 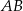 . Jakie współrzędne ma punkt B?
. Jakie współrzędne ma punkt B? 
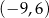
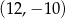
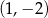
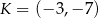 oraz
oraz 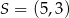 . Punkt
. Punkt 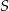 jest środkiem odcinka
jest środkiem odcinka 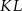 . Wtedy punkt
. Wtedy punkt 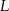 ma współrzędne
ma współrzędne 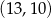
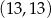
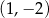
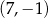
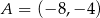 i
i 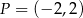 . Punkt
. Punkt 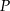 jest środkiem odcinka
jest środkiem odcinka 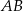 . Jakie współrzędne ma punkt
. Jakie współrzędne ma punkt 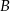 ?
? 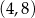
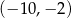
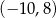
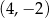
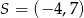 jest środkiem odcinka
jest środkiem odcinka 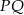 , gdzie
, gdzie 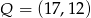 . Zatem punkt
. Zatem punkt 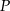 ma współrzędne
ma współrzędne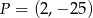
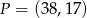
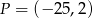
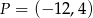
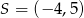 jest środkiem odcinka
jest środkiem odcinka 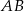 i
i 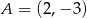 . Punkt
. Punkt 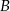 ma współrzędne
ma współrzędne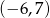
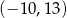
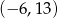
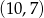
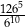 jest równy A/B.
jest równy A/B.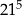
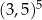
 jest równy C/D.
jest równy C/D.