Na uszycie 90 jednakowych bluzek w rozmiarze 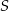 potrzeba tyle samo materiału, ile na uszycie 60 jednakowych bluzek w rozmiarze
potrzeba tyle samo materiału, ile na uszycie 60 jednakowych bluzek w rozmiarze 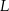 . Przyjmij, że na uszycie większej lub mniejszej liczby bluzek potrzeba proporcjonalnie więcej lub mniej materiału.
. Przyjmij, że na uszycie większej lub mniejszej liczby bluzek potrzeba proporcjonalnie więcej lub mniej materiału.
Na uszycie 240 bluzek w rozmiarze 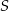 potrzeba tyle samo materiału, ile potrzeba na uszycie A/B bluzek w rozmiarze
potrzeba tyle samo materiału, ile potrzeba na uszycie A/B bluzek w rozmiarze 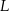 .
.
A) 160 B) 150
Na uszycie dwóch bluzek w rozmiarze 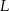 potrzeba tyle samo materiału, ile potrzeba na uszycie C/D bluzek w rozmiarze
potrzeba tyle samo materiału, ile potrzeba na uszycie C/D bluzek w rozmiarze 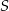 .
.
C) trzech D) pięciu
/Szkoła podstawowa/Zadania testowe/Zadania z treścią
Na uszycie 120 jednakowych czapek w rozmiarze 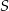 potrzeba tyle samo materiału, ile na uszycie 90 jednakowych czapek w rozmiarze
potrzeba tyle samo materiału, ile na uszycie 90 jednakowych czapek w rozmiarze 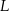 . Przyjmij, że na uszycie większej lub mniejszej liczby czapek potrzeba proporcjonalnie więcej lub mniej materiału.
. Przyjmij, że na uszycie większej lub mniejszej liczby czapek potrzeba proporcjonalnie więcej lub mniej materiału.
Na uszycie 160 czapek w rozmiarze 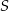 potrzeba tyle samo materiału, ile potrzeba na uszycie A/B czapek w rozmiarze
potrzeba tyle samo materiału, ile potrzeba na uszycie A/B czapek w rozmiarze 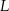 .
.
A) 150 B) 120
Na uszycie trzech czapek w rozmiarze 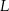 potrzeba tyle samo materiału, ile potrzeba na uszycie C/D czapek w rozmiarze
potrzeba tyle samo materiału, ile potrzeba na uszycie C/D czapek w rozmiarze 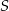 .
.
C) czterech D) pięciu
Słoń indyjski osiąga masę od 3,5 do 5 ton i zjada dziennie około 150 kg pokarmu. Na ile co najmniej dni wystarczy 5 ton pokarmu dla 4 słoni indyjskich?
A) 8 B) 9 C) 33 D) 34
Pracownicy oczyszczalni ścieków przeprowadzili operację napełniania 4 zbiorników. Zbiorniki napełniano kolejno i na diagramie przedstawiono w procentach jaką część czasu zajęło napełnianie kolejnych zbiorników. Zbiornik nr 2 napełniono w ciągu 24 minut.
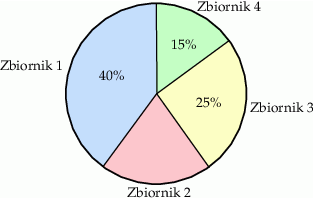
Ile minut trwało napełnianie zbiornika nr 4?
A) 18 minut B) 15 minut C) 16 minut D) 20 minut
Na rysunku przedstawiono cztery kartki ze starych kalendarzy – dwie z nich pochodzą z kalendarza z roku 1982, jedna z roku 1981, jedna z roku 1983.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W 1982 roku 4 lipca wypadł sobotę. | P | F |
| W 1981 roku 15 czerwca wypadł w poniedziałek. | P | F |
Basen ma kształt prostopadłościanu, którego podstawa (dno basenu) ma wymiary 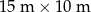 . Do basenu wlano
. Do basenu wlano 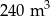 wody, która wypełniła go do
wody, która wypełniła go do  głębokości.
głębokości.
Jaka jest głębokość tego basenu?
A) 1,28 m B) 1,5 m C) 2 m D) 3 m
Zbiornik na wodę ma kształt walca, którego podstawa (dno zbiornika) ma średnicę 10 m. Do zbiornika wlano 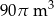 wody, która wypełniła go do
wody, która wypełniła go do  głębokości.
głębokości.
Jaka jest głębokość tego zbiornika?
A) 8 m B) 18 m C) 2 m D) 6 m
Zbiornik retencyjny ma kształt walca o wysokości 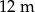 . Do zbiornika wlano
. Do zbiornika wlano 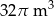 wody, która wypełniła go do
wody, która wypełniła go do  wysokości.
wysokości.
Jaka jest średnica podstawy tego zbiornika?
A) 0,5 m B) 1 m C) 2 m D) 4 m
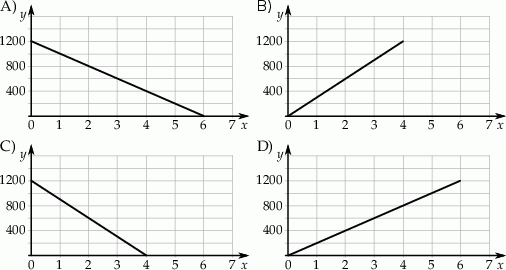
Wzór 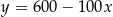 opisuje zależność objętości
opisuje zależność objętości 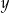 (w litrach) wody w zbiorniku od czasu
(w litrach) wody w zbiorniku od czasu  (w minutach) upływającego podczas opróżniania tego zbiornika. Który wykres przedstawia tę zależność?
(w minutach) upływającego podczas opróżniania tego zbiornika. Który wykres przedstawia tę zależność?
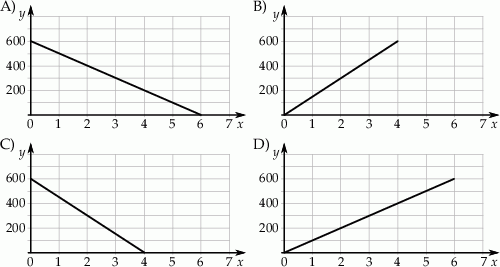
Na stacji paliw zatankowano do pełna 70 litrowy bak samochodu. Okazało się, że do baku wlano 60 litrów paliwa przy przepływie 10 litrów na minutę. Który wykres przedstawia zależność ilości litrów paliwa w baku od czasu nalewania w minutach?
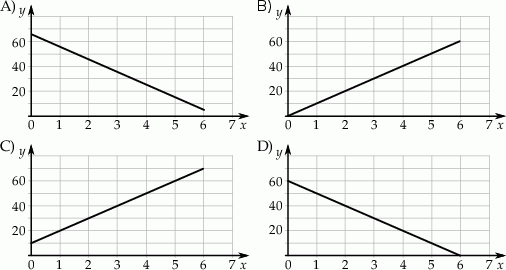
Wzór  opisuje zależność objętości
opisuje zależność objętości  (w litrach) wody w zbiorniku od czasu
(w litrach) wody w zbiorniku od czasu  (w minutach) upływającego podczas opróżniania tego zbiornika. Który wykres przedstawia tę zależność?
(w minutach) upływającego podczas opróżniania tego zbiornika. Który wykres przedstawia tę zależność?
Na diagramie przedstawiono liczbę butelek z wodą dostarczonych do sklepu osiedlowego oraz liczbę butelek z wodą sprzedanych w tym sklepie przez trzy kolejne dni: poniedziałek, wtorek i środę.
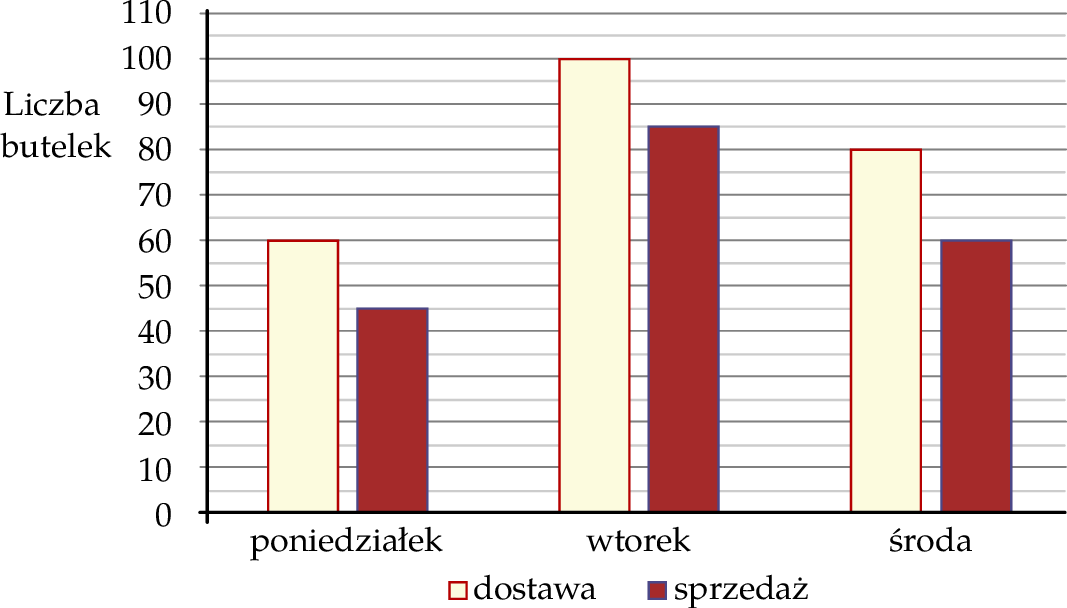
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przez te trzy dni w sklepie osiedlowym sprzedano łącznie 190 butelek z wodą. | P | F |
Liczba butelek z wodą sprzedanych w poniedziałek stanowi  liczby butelek z wodą dostarczonych w tym dniu. liczby butelek z wodą dostarczonych w tym dniu. | P | F |
W zawodach sportowych każdy zawodnik miał pokonać trasę składającą się z trzech części. Pierwszą część trasy zawodnik przejechał na rowerze, drugą część – prowadzącą przez jezioro – przepłynął, a trzecią – przebiegł. Na rysunku przedstawiono schemat tej trasy.
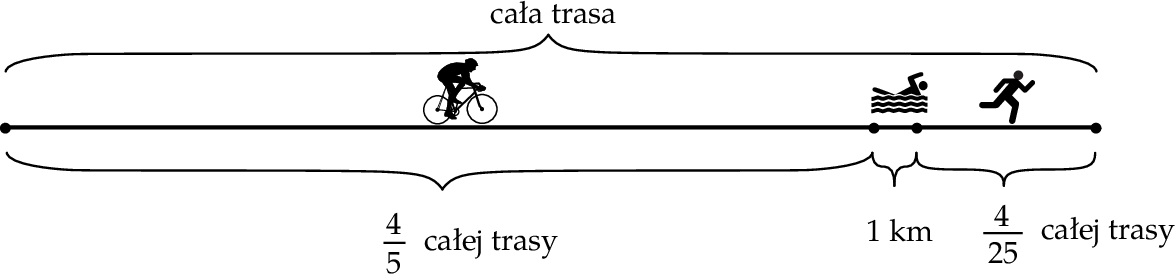
A) Cała trasa miała długość 50 km.
B) Zawodnik przebiegł 8 km.
C) Odległość, którą zawodnik przebiegł, była o 4 km większa od odległości, którą przepłynął.
D) Odległość, którą zawodnik przejechał na rowerze, była 5 razy większa od odległości, którą przebiegł.
W zawodach sportowych każdy zawodnik miał pokonać trasę składającą się z trzech części. Pierwszą część trasy zawodnik przejechał na rowerze, drugą część – prowadzącą przez jezioro – przepłynął, a trzecią – przebiegł. Na rysunku przedstawiono schemat tej trasy.
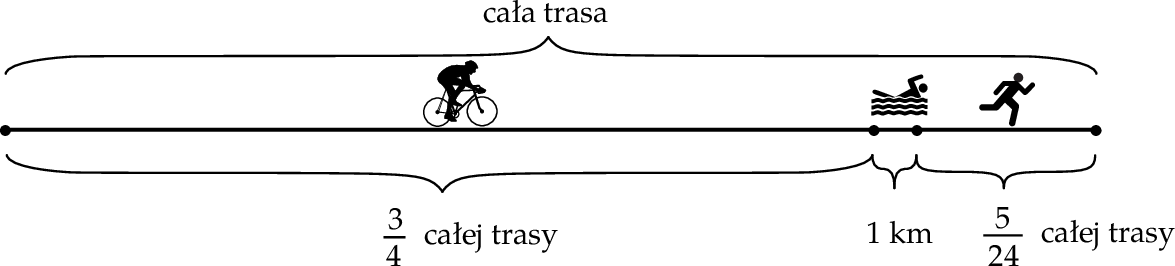
A) Cała trasa miała długość 48 km.
B) Zawodnik przebiegł 10 km.
C) Odległość, którą zawodnik przebiegł, była o 4 km większa od odległości, którą przepłynął.
D) Odległość, którą zawodnik przejechał na rowerze, była 4 razy większa od odległości, którą przebiegł.
Klasa IIIf wybrała się na wycieczkę składającą się z trzech części. W pierwszej części uczniowie zostali zawiezieni autokarem na miejsce, w którym rozpoczęła się ich piesza wędrówka. W drugiej części odbyli spacer górskim szlakiem, a w ostatniej części zwiedzali leśną ścieżkę dydaktyczną. Na rysunku przedstawiono schemat przebiegu wycieczki.

A) Cała trasa miała długość 54 km.
B) Uczniowie pokonali autobusem 30 km.
C) Leśna ścieżka dydaktyczna była o 5 km dłuższa od górskiego szlaku.
D) Długość górskiego szlaku była 3 razy mniejsza niż długość leśnej ścieżki dydaktycznej.
Klasa Ib wybrała się na wycieczkę składającą się z trzech części. W pierwszej części uczniowie zostali zawiezieni autokarem na miejsce, w którym rozpoczęła się ich piesza wędrówka. W drugiej części odbyli spacer górskim szlakiem, a w ostatniej części zwiedzali leśną ścieżkę dydaktyczną. Na rysunku przedstawiono schemat przebiegu wycieczki.

A) Cała trasa miała długość 50 km.
B) Uczniowie pokonali autobusem 36 km.
C) Leśna ścieżka dydaktyczna była o 8 km dłuższa od górskiego szlaku.
D) Długość górskiego szlaku była 3 razy mniejsza niż długość leśnej ścieżki dydaktycznej.
Dwaj kolarze pokonali linię mety wyścigu kolarskiego z tą samą prędkością 54 km/h, przy czym pierwszy z nich minął linię mety o pół sekundy wcześniej niż drugi kolarz. O ile metrów pierwszy kolarz wyprzedzał drugiego podczas przekraczania linii mety?
A) 7,5 m B) 15 m C) 10 m D) 9 m
W pewnym sklepie papiernicznym za 350 kopert trzeba zapłacić 63 zł. Przy zakupie przekraczającym 1000 kopert otrzymuje się rabat w wysokości 10%.
Ile trzeba zapłacić za 1200 kopert w tym sklepie?
A) 194,4 zł B) 213,84 zł C) 216 zł D) 237,6 zł
Rozmiar ramy roweru to długość fragmentu rury pod siodełkiem mierzona tak, jak przedstawiono na rysunku – od środka miejsca, w którym obracają się pedały do środka rury łączącej siodełko z kierownicą.
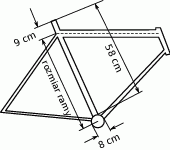
Jaki jest rozmiar ramy, której niektóre wymiary przedstawiono na rysunku?
A) 49 cm B) 53 cm C) 58 cm D) 59 cm
Pan Nowak postanowił kupić wykładzinę na prostokątną podłogę o wymiarach 3 m i 4 m. Pod uwagę wziął dwa typy wykładziny.
| Typ wykładziny | Szerokość wykładziny | Cena wykładziny |
| welurowa | 4 m | 35 zł za 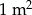 |
| wełniana | 3 m | 95 zł za 1 metr bieżący |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cena 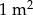 wykładziny welurowej jest niższa niż cena wykładziny welurowej jest niższa niż cena 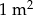 wykładziny wełnianej. wykładziny wełnianej. | P | F |
| Kupując tańszą wykładzinę, pan Nowak zaoszczędzi 40 zł. | P | F |
Pan Tadeusz postanowił pomalować ściany w swoim mieszkaniu. Łączna powierzchnia ścian, które postanowił pomalować jest równa 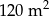 . Pod uwagę wziął dwa rodzaje farb.
. Pod uwagę wziął dwa rodzaje farb.
| Rodzaj farby | Wydajność | Cena |
| Fabra lateksowa | 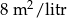 | 5 zł za 1 litr |
| Farba akrylowa | 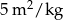 | 3 zł za 1 kg |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Koszt pomalowania 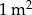 ściany jest niższy w przypadku farby akrylowej, niż w przypadku farby lateksowej. ściany jest niższy w przypadku farby akrylowej, niż w przypadku farby lateksowej. | P | F |
| Kupując tańszą farbę, pan Tadeusz zaoszczędzi 5 zł. | P | F |
Pan Kazimierz chce kupić 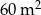 papy. Papa jest sprzedawana w rolkach o szerokości 1 m. Pan Kazimierz pod uwagę wziął dwa rodzaje papy.
papy. Papa jest sprzedawana w rolkach o szerokości 1 m. Pan Kazimierz pod uwagę wziął dwa rodzaje papy.
| Typ papy | Długość papy w rolce | Cena papy |
| I rodzaj | 15 m | 75 zł za 1 rolkę |
| II rodzaj | 3 m | 6 zł za 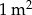 |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cena 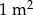 papy I rodzaju jest niższa niż cena papy I rodzaju jest niższa niż cena 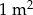 papy II rodzaju. papy II rodzaju. | P | F |
| Kupując tańszą papę, pan Kazimierz zaoszczędzi 40 zł. | P | F |
Pole działki budowlanej jest równe 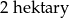 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 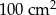 B)
B) 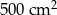 C)
C) 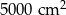 D)
D) 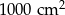
Pole działki budowlanej jest równe 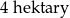 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 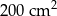 B)
B) 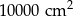 C)
C) 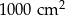 D)
D) 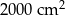
Do prostopadłościennego akwarium, o wymiarach podanych na rysunku, wlano 400 litrów wody.
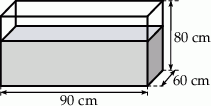
Czy włożenie do akwarium metalowego sześcianu o krawędzi 32 cm sprawi, że część wody się wyleje? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | objętość sześcianu jest mniejsza niż 40 litrów. |
| B) | objętość sześcianu jest większa niż 32 litry. |
| C) | długość krawędzi sześcianu jest mniejsza od długości każdej krawędzi akwarium. |
Wujek Kasi odbył podróż pociągiem z Krakowa do Koszalina. W tabeli przedstawiono niektóre dane dotyczące tej podróży: czasy odjazdu, przyjazdu oraz czas na przesiadkę.
| Kraków | Warszawa | Przes. | Warszawa | Gdynia | Przes. | Gdynia | Koszalin |
| 16:50 | 19:14 | 11 min. | 19:25 | 127 min. | 0:58 | 3:32 |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wujek Kasi przyjechał do Gdyni o godz. 22:45. | P | F |
| Cała podróż z Krakowa do Koszalina trwała 10 godzin i 42 minuty. | P | F |
Średnia prędkość samochodu na trasie przebytej w czasie 4 godzin wyniosła 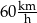 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Aby czas przejazdu był o 1 godzinę krótszy, średnia prędkość samochodu na tej trasie musiałaby wynosić 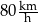 . . | P | F |
Gdyby średnia prędkość samochodu na tej trasie była równa 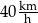 , to czas przejazdu byłby równy 6 godzin. , to czas przejazdu byłby równy 6 godzin. | P | F |
Średnia prędkość samochodu na trasie przebytej w czasie 3 godzin wyniosła 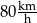 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Aby czas przejazdu był o 1 godzinę krótszy, średnia prędkość samochodu na tej trasie musiałaby wynosić 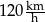 . . | P | F |
Gdyby średnia prędkość samochodu na tej trasie była równa 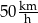 , to czas przejazdu byłby równy 5 godzin. , to czas przejazdu byłby równy 5 godzin. | P | F |
Pociąg towarowy pokonał trasę o długości 360 km w czasie 4,5 godziny.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Gdyby średnia prędkość pociągu była większa o 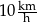 , to pociąg pokonałby tę trasę w czasie o 30 minut krótszym. , to pociąg pokonałby tę trasę w czasie o 30 minut krótszym. | P | F |
| Gdyby pociąg poruszał się z tą samą prędkością średnią, to trasę długości 450 km przebyłby w czasie 5,5 godziny. | P | F |
W pewnej hurtowni za 120 jednakowych długopisów i 360 jednakowych ołówków zapłacono 600 zł. Jaka byłaby cena zakupu 170 takich samych długopisów i 510 takich samych ołówków w tej hurtowni?
A) 850 zł B) 800 zł C) 780 zł D) 680 zł
Na wycieczkę szkolną pojechali uczniowie dwóch klas: klasy IIa i IIb. Liczba uczniów klasy IIa stanowi  liczby uczniów klasy IIb. Ponadto
liczby uczniów klasy IIb. Ponadto  uczniów każdej z klas stanowią dziewczęta. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
uczniów każdej z klas stanowią dziewczęta. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na wycieczkę pojechało dwa razy więcej dziewcząt niż chłopców. | P | F |
| Na wycieczkę pojechało 3 razy więcej uczniów klasy IIb niż klasy IIa. | P | F |
Działka ma powierzchnię 200 arów. Warzywa zajmują 130 arów, jabłonie rosną na 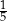 pozostałej części działki, a resztę działki zajmują śliwy. Śliwy zajmują powierzchnię
pozostałej części działki, a resztę działki zajmują śliwy. Śliwy zajmują powierzchnię
A) 14 arów. B) 30 arów. C) 56 arów. D) 70 arów.
Prędkość średnia piechura na trasie 10 km wyniosła 5 km/h, a prędkość średnia rowerzysty na tej samej trasie była równa 20 km/h. O ile minut więcej zajęło pokonanie tej trasy piechurowi niż rowerzyście?
A) 30 minut B) 60 minut C) 90 minut D) 120 minut
Prędkość średnia samochodu osobowego na odcinku autostrady długości 50 km wyniosła 120 km/h, a prędkość średnia motocyklisty na tym samym odcinku autostrady wyniosła 100 km/h. O ile minut więcej zajęło pokonanie tego odcinka autostrady motocykliście niż kierowcy samochodu osobowego?
A) 4 minuty B) 5 minut C) 6 minut D) 8 minut
Prędkość średnia piechura na trasie 20 km wyniosła 5 km/h, a prędkość średnia rowerzysty na tej samej trasie była równa 10 km/h. O ile minut więcej zajęło pokonanie tej trasy piechurowi niż rowerzyście?
A) 180 minut B) 120 minut C) 90 minut D) 60 minut
Prędkość średnia piechura na trasie 9 km wyniosła 6 km/h, a prędkość średnia rowerzysty na tej samej trasie była równa 18 km/h. O ile minut więcej zajęło pokonanie tej trasy piechurowi niż rowerzyście?
A) 30 minut B) 60 minut C) 90 minut D) 120 minut

