Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest półkolem. Oblicz miarę kąta rozwarcia stożka.
/Szkoła średnia/Geometria/Stereometria/Stożek/Kąt
Hania zaprojektowała i wykonała czapeczkę na bal urodzinowy młodszego brata. Czapeczka miała kształt powierzchni bocznej stożka o średnicy podstawy 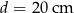 , wysokości
, wysokości 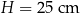 i tworzącej
i tworzącej 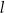 . Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską
. Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską 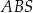 o kształcie wycinka koła o promieniu
o kształcie wycinka koła o promieniu 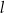 i środku
i środku 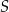 . Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek
. Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek 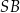 z odcinkiem
z odcinkiem 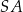 .
.

Oblicz miarę kąta 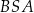 wycinka koła, z którego powstała powierzchnia boczna stożka. Miarę kąta
wycinka koła, z którego powstała powierzchnia boczna stożka. Miarę kąta 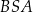 podaj w zaokrągleniu do jednego stopnia.
podaj w zaokrągleniu do jednego stopnia.
Pole powierzchni całkowitej stożka jest trzy razy większe od pola jego podstawy. Oblicz miarę kąta rozwarcia tego stożka.
Wysokość walca wpisanego w stożek jest równa promieniowi podstawy stożka. Stosunek objętości stożka do objętości walca wynosi 8 : 3. Oblicz tangens kąta zawartego między wysokością a tworzącą stożka.
Pole powierzchni całkowitej 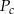 stożka oraz jego pole podstawy
stożka oraz jego pole podstawy 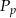 spełniają równanie
spełniają równanie 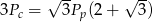 . Oblicz miarę kąta rozwarcia stożka.
. Oblicz miarę kąta rozwarcia stożka.
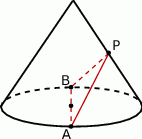
Środek 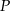 tworzącej stożka połączono z końcami
tworzącej stożka połączono z końcami 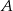 i
i 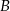 średnicy koła w podstawie stożka tak, że
średnicy koła w podstawie stożka tak, że 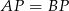 . Wiedząc, że kąt rozwarcia stożka jest równy
. Wiedząc, że kąt rozwarcia stożka jest równy 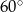 , oblicz kąty trójkąta
, oblicz kąty trójkąta 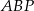 .
.
Stosunek pola powierzchni bocznej stożka do pola przekroju osiowego tego stożka jest równy 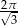 . Oblicz kąt rozwarcia stożka.
. Oblicz kąt rozwarcia stożka.
Stosunek pola powierzchni bocznej stożka do pola przekroju osiowego tego stożka jest równy 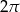 . Oblicz kąt rozwarcia stożka.
. Oblicz kąt rozwarcia stożka.
Tworząca stożka ma długość 3 dm. Długość promienia podstawy stożka jest równa 1 dm. Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest wycinkiem koła. Oblicz miarę  kąta środkowego tego wycinka.
kąta środkowego tego wycinka.
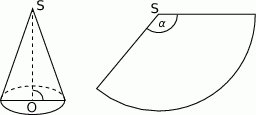
Stosunek pola powierzchni bocznej stożka do pola jego powierzchni całkowitej jest równy  . Wyznacz miarę kąta nachylenia tworzącej stożka do płaszczyzny podstawy.
. Wyznacz miarę kąta nachylenia tworzącej stożka do płaszczyzny podstawy.
Objętość stożka o wysokości 2 jest równa 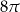 . Oblicz miarę kąta rozwarcia tego stożka.
. Oblicz miarę kąta rozwarcia tego stożka.
Odległość środka wysokości stożka od jego powierzchni bocznej jest trzy razy mniejsza niż promień jego podstawy. Oblicz sinus kąta rozwarcia stożka.
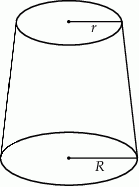
Objętość stożka ściętego (przedstawionego na rysunku) można obliczyć ze wzoru 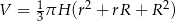 , gdzie
, gdzie  i
i 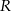 są promieniami podstaw (
są promieniami podstaw (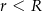 ), a
), a 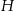 jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość
jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość 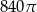 , a
, a 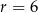 . Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.
. Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.