Oblicz pole wycinka koła o środku w punkcie 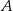 (zacieniowany obszar) jeśli pole rombu
(zacieniowany obszar) jeśli pole rombu 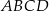 wynosi
wynosi 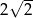 , a kąt ostry rombu ma miarę
, a kąt ostry rombu ma miarę 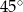 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
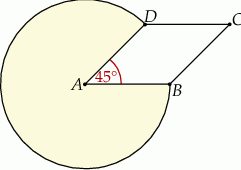
Oblicz pole wycinka koła o środku w punkcie 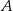 (zacieniowany obszar) jeśli pole rombu
(zacieniowany obszar) jeśli pole rombu 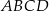 wynosi
wynosi 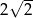 , a kąt ostry rombu ma miarę
, a kąt ostry rombu ma miarę 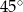 .
.

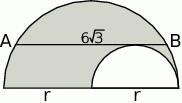
Z półkola o promieniu  wycięto półkole o średnicy
wycięto półkole o średnicy  (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 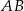 jest styczna do mniejszego półkola i jest równoległa do średnicy większego półkola. Oblicz pole zacieniowanego obszaru.
jest styczna do mniejszego półkola i jest równoległa do średnicy większego półkola. Oblicz pole zacieniowanego obszaru.
W półkolu z końca średnicy poprowadzono cięciwę, która tworzy ze średnicą kąt o mierze 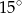 . Oblicz w jakim stosunku zostało podzielone pole tego półkola.
. Oblicz w jakim stosunku zostało podzielone pole tego półkola.
Kąt wpisany w koło ma miarę 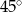 i jest oparty na łuku długości
i jest oparty na łuku długości 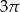 . Oblicz pole wycinka koła wyznaczonego przez ten sam łuk.
. Oblicz pole wycinka koła wyznaczonego przez ten sam łuk.
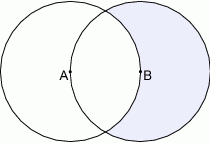
Na rysunku przedstawiono dwa koła o promieniu 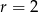 takie, że środek każdego z kół leży na brzegu drugiego koła. Oblicz pole powierzchni zacieniowanej części tej figury.
takie, że środek każdego z kół leży na brzegu drugiego koła. Oblicz pole powierzchni zacieniowanej części tej figury.
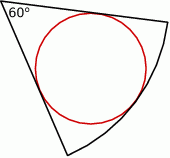
W wycinek koła o kącie 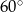 wpisano okrąg o promieniu 2 cm. Oblicz pole tego wycinka.
wpisano okrąg o promieniu 2 cm. Oblicz pole tego wycinka.
Trójkąt 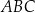 jest trójkątem równobocznym o boku długości 2. Obszar
jest trójkątem równobocznym o boku długości 2. Obszar 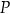 jest zawarty między półokręgiem o średnicy
jest zawarty między półokręgiem o średnicy 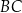 i łukiem okręgu o środku
i łukiem okręgu o środku 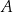 przechodzącym przez punkty
przechodzącym przez punkty 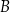 i
i 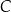 . Oblicz pole obszaru
. Oblicz pole obszaru 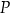 .
.
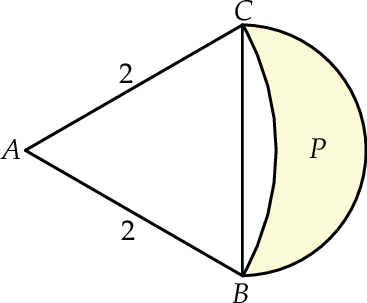
Koło 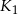 ma promień długości
ma promień długości  . Wewnątrz tego koła rysujemy kolejno koła
. Wewnątrz tego koła rysujemy kolejno koła 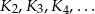 takie, że kolejne koło ma średnicę równą promieniowi poprzedniego koła.
takie, że kolejne koło ma średnicę równą promieniowi poprzedniego koła.
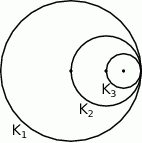
Wyznacz pole koła 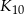 .
.
