Suma liczby odwrotnej do 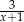 i przeciwnej do
i przeciwnej do 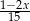 jest równa
jest równa
A) 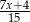 B)
B) 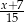 C)
C) 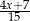 D)
D) 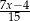
/Szkoła podstawowa/Zadania testowe/Wyrażenia algebraiczne/1 literka
W naczyniu znajdowało się 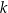 litrów wody. Marcin odlał z tego naczynia
litrów wody. Marcin odlał z tego naczynia 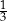 tej objętości wody, a następnie Magda odlała 3 litry wody. Objętość wody wyrażoną w litrach, która pozostała w naczyniu, opisuje wyrażenie
tej objętości wody, a następnie Magda odlała 3 litry wody. Objętość wody wyrażoną w litrach, która pozostała w naczyniu, opisuje wyrażenie
A) 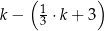 B)
B) 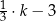 C)
C) 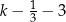 D)
D) 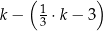
Po wykonaniu działań w wyrażeniu 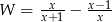 otrzymujemy
otrzymujemy
A) 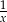 B)
B) 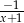 C)
C) 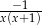 D)
D) 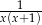
Wyrażenie 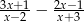 jest równe
jest równe
A) 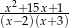 B)
B) 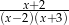 C)
C) 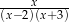 D)
D) 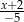
Wyrażenie 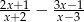 jest równe
jest równe
A) 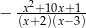 B)
B) 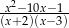 C)
C) 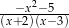 D)
D) 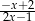
Po wykonaniu działania 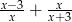 otrzymujemy
otrzymujemy
A) 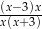 B)
B) 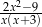 C)
C) 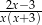 D)
D) 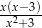
Wyrażenie 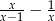 , określone dla
, określone dla 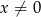 i
i 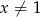 , jest równe
, jest równe
A) 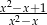 B)
B) 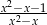 C)
C) 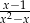 D)
D) 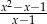
Po wykonaniu działań w wyrażeniu 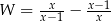 otrzymujemy
otrzymujemy
A) 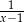 B)
B) 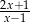 C)
C) 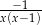 D)
D) 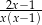
Wyrażenie 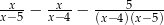 można zapisać w postaci
można zapisać w postaci
A) 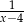 B)
B) 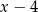 C)
C) 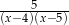 D)
D) 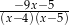
Jacek ma o 4 lata młodszego brata Kamila, który ma  lat. Kamil ma koleżankę Basię, która jest od niego dwa razy starsza. Różnica wieku Basi i Jacka jest równa
lat. Kamil ma koleżankę Basię, która jest od niego dwa razy starsza. Różnica wieku Basi i Jacka jest równa
A) 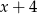 B)
B) 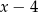 C)
C)  D)
D) 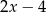
Tomek otrzymał torebkę, w której było  cukierków. Sam zjadł z tej torebki 8 cukierków, a pozostałe cukierki rozdzielił pomiędzy swoich 5 kolegów. Czworo z tych chłopców otrzymało tyle samo cukierków, a piąty z nich, Szymon, otrzymał o jeden cukierek więcej od pozostałych. Liczba cukierków, które otrzymał Szymon jest równa
cukierków. Sam zjadł z tej torebki 8 cukierków, a pozostałe cukierki rozdzielił pomiędzy swoich 5 kolegów. Czworo z tych chłopców otrzymało tyle samo cukierków, a piąty z nich, Szymon, otrzymał o jeden cukierek więcej od pozostałych. Liczba cukierków, które otrzymał Szymon jest równa
A) 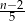 B)
B) 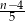 C)
C) 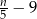 D)
D) 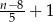
Iloczyn 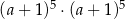 jest równy
jest równy
A) 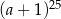 B)
B) 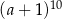 C)
C) 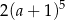 D)
D) 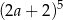
W pudełku są kulki czerwone, zielone i niebieskie. Kulek czerwonych jest trzy razy więcej niż zielonych i o dwie mniej niż niebieskich. W pudełku najmniej jest kulek A/B.
A) niebieskich B) zielonych
Jeśli liczbę kulek zielonych oznaczymy przez  , to liczbę wszystkich kulek w pudełku opisuje wyrażenie C/D.
, to liczbę wszystkich kulek w pudełku opisuje wyrażenie C/D.
C) 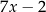 D)
D) 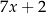
Zdanie „różnica kwadratów dwóch kolejnych liczb naturalnych nieparzystych jest niemniejsza niż 5” przedstawiono w postaci nierówności:
A) 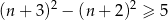 B)
B) 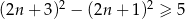
C) 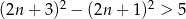 D)
D) ![2 [(2n + 3) − (2n + 1 )] ≥ 5](https://img.zadania.info/zad/3694791/HzadT3x.gif)
Zdanie „kwadrat różnicy dwóch kolejnych liczb naturalnych nieparzystych jest niemniejszy niż 5” można zapisać w postaci nierówności:
A) ![[(n + 3) − (n + 2)]2 ≥ 5](https://img.zadania.info/zad/5555770/HzadT0x.gif) B)
B) 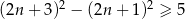
C) 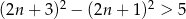 D)
D) ![2 [(2n + 3) − (2n + 1 )] ≥ 5](https://img.zadania.info/zad/5555770/HzadT3x.gif)
Dane są trzy wyrażenia:
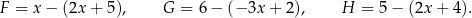
Dla każdej wartości  prawdziwa jest równość
prawdziwa jest równość
A) 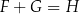 B)
B) 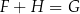 C)
C) 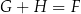 D)
D) 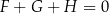
Liczba przeciwna do podwojonej odwrotności liczby  jest równa
jest równa
A) 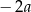 B)
B) 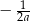 C)
C) 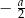 D)
D) 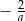
Liczba odwrotna do podwojonej odwrotności liczby  jest równa
jest równa
A) 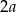 B)
B) 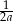 C)
C) 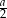 D)
D) 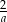
Liczba przeciwna do potrojonej odwrotności liczby  jest równa
jest równa
A) 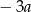 B)
B) 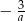 C)
C) 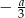 D)
D) 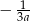
Połowę liczby  zmniejszono o 3, a następnie do otrzymanego wyniku dodano dwukrotność liczby
zmniejszono o 3, a następnie do otrzymanego wyniku dodano dwukrotność liczby 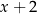 . W wyniku tych działań otrzymano wyrażenie
. W wyniku tych działań otrzymano wyrażenie
A) 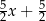 B)
B) 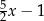 C)
C) 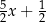 D)
D) 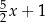
Wartość wyrażenia 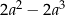 dla
dla 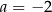 jest równa A/B.
jest równa A/B.
A) 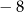 B) 24
B) 24
Wyrażenie 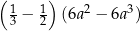 można przekształcić do postaci C/D.
można przekształcić do postaci C/D.
C) 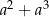 D)
D) 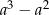
Suma wyrażeń 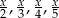 jest równa
jest równa
A) 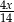 B)
B) 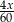 C)
C) 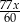 D)
D) 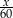
Dane są cztery wyrażenia:

Jedno z tych wyrażeń przyjmuje wartość 0 dla 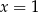 oraz dla
oraz dla 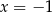 . Które to wyrażenie?
. Które to wyrażenie?
A) 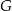 B)
B) 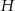 C)
C) 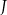 D)
D) 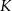
Dane są cztery wyrażenia:

Jedno z tych wyrażeń przyjmuje wartość 0 dla 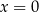 oraz dla
oraz dla 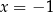 . Które to wyrażenie?
. Które to wyrażenie?
A) 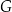 B)
B) 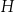 C)
C) 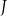 D)
D) 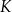
Dane są cztery wyrażenia:

Jedno z tych wyrażeń przyjmuje tą samą wartość dla 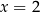 oraz dla
oraz dla 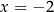 . Które to wyrażenie?
. Które to wyrażenie?
A) 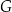 B)
B) 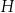 C)
C) 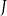 D)
D) 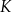
Wartość wyrażenia 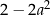 dla
dla 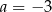 jest równa A/B.
jest równa A/B.
A) 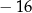 B) 20
B) 20
Wyrażenie 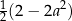 można przekształcić do postaci C/D.
można przekształcić do postaci C/D.
C) 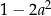 D)
D) 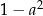
Wartość wyrażenia 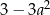 dla
dla 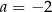 jest równa A/B.
jest równa A/B.
A) 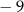 B) 15
B) 15
Wyrażenie 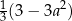 można przekształcić do postaci C/D.
można przekształcić do postaci C/D.
C) 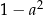 D)
D) 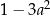
Wartością wyrażenia 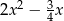 dla
dla 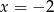 jest liczba:
jest liczba:
A) 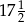 B)
B) 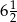 C)
C) 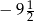 D)
D) 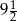
Dla każdej liczby rzeczywistej 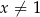 wyrażenie
wyrażenie 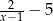 jest równe
jest równe
A) 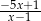 B)
B) 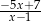 C)
C) 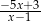 D)
D) 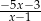
Dla każdej liczby rzeczywistej  różnej od 0 wartość wyrażenia
różnej od 0 wartość wyrażenia 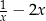 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A)  B)
B) 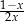 C)
C) 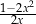 D)
D) 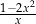
Dla każdej liczby rzeczywistej 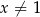 wyrażenie
wyrażenie 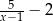 jest równe
jest równe
A) 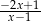 B)
B) 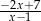 C)
C) 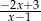 D)
D) 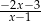
Dla każdej liczby rzeczywistej  różnej od 0 wartość wyrażenia
różnej od 0 wartość wyrażenia 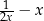 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A)  B)
B) 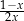 C)
C) 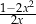 D)
D) 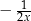
Dane jest wyrażenie 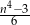 oraz liczby:
oraz liczby: 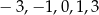 . Dla której z danych liczb wartość podanego wyrażenia jest najmniejsza?
. Dla której z danych liczb wartość podanego wyrażenia jest najmniejsza?
A) 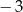 B)
B) 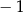 C) 0 D) 1 E) 3
C) 0 D) 1 E) 3
Dane jest wyrażenie 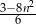 oraz liczby:
oraz liczby: 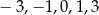 . Dla której z danych liczb wartość podanego wyrażenia jest największa?
. Dla której z danych liczb wartość podanego wyrażenia jest największa?
A) 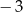 B)
B) 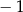 C) 0 D) 1 E) 3
C) 0 D) 1 E) 3
Wyrażenie 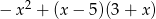 można przekształcić do postaci
można przekształcić do postaci
A) 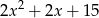 B)
B) 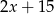 C)
C) 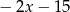 D)
D) 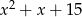
Wyrażenie 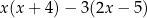 można przekształcić równoważnie do postaci
można przekształcić równoważnie do postaci
A) 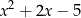 B)
B) 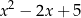 C)
C) 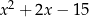 D)
D) 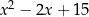
Wyrażenie 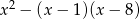 można przekształcić do postaci
można przekształcić do postaci
A) 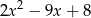 B)
B) 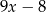 C)
C) 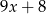 D)
D) 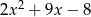
Wyrażenie 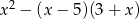 można przekształcić do postaci
można przekształcić do postaci
A) 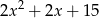 B)
B) 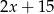 C)
C) 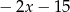 D)
D) 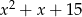
Wartość wyrażenia algebraicznego
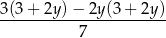
obliczono dla pięciu różnych wartości 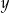 :
:
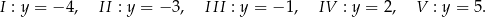
Największą wartość wyrażenia otrzymano w przypadku A/B.
A) I B) III
Najmniejszą wartość wyrażenia otrzymano w przypadku C/D.
C) II D) V

