Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek 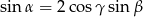 to trójkąt ten jest równoramienny.
to trójkąt ten jest równoramienny.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
W trójkącie ostrokątnym 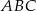 bok
bok 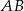 ma długość
ma długość  , długość boku
, długość boku 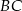 jest równa
jest równa  oraz
oraz 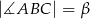 . Dwusieczna kąta
. Dwusieczna kąta 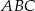 przecina bok
przecina bok 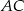 trójkąta w punkcie
trójkąta w punkcie 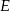 . Wykaż, że długość odcinka
. Wykaż, że długość odcinka 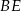 jest równa
jest równa 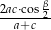 .
.
Uzasadnij, że jeżeli 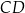 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 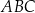 , w którym
, w którym 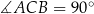 to
to 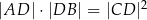 .
.

Na bokach trójkąta równobocznego zbudowano dwa kwadraty w sposób pokazany na rysunku.
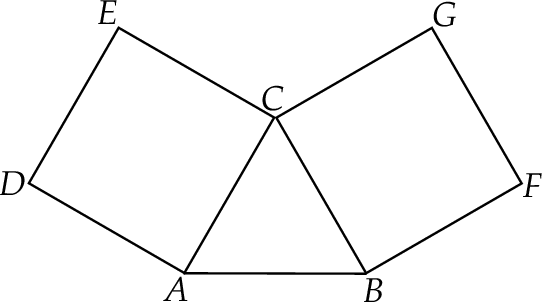
Wykaż, że punkty 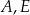 i
i 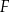 są wierzchołkami trójkąta prostokątnego.
są wierzchołkami trójkąta prostokątnego.
Przyprostokątne trójkąta prostokątnego 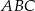 mają długości 10 i 24. Przeciwprostokątna trójkąta
mają długości 10 i 24. Przeciwprostokątna trójkąta 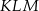 podobnego do niego ma długość 39. Oblicz pole trójkąta
podobnego do niego ma długość 39. Oblicz pole trójkąta 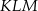 .
.
Trójkąty prostokątne 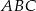 i
i 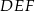 są podobne. Przyprostokątne trójkąta
są podobne. Przyprostokątne trójkąta 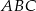 mają długości 5 i 12, a przeciwprostokątna trójkąta
mają długości 5 i 12, a przeciwprostokątna trójkąta 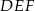 ma długość 26. Wyznacz pole trójkąta
ma długość 26. Wyznacz pole trójkąta 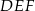 .
.
Przyprostokątne trójkąta prostokątnego 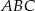 mają długości 9 i 40. Najdłuższy bok tego trójkąta jest równy najkrótszemu bokowi trójkąta
mają długości 9 i 40. Najdłuższy bok tego trójkąta jest równy najkrótszemu bokowi trójkąta 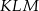 podobnego do trójkąta
podobnego do trójkąta 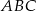 . Oblicz pole trójkąta
. Oblicz pole trójkąta 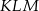 .
.
Dwa krótsze boki trójkąta rozwartokątnego mają długości 5 cm i 6 cm. Jakie wartości może przyjmować długość trzeciego boku trójkąta?
Odcinek 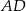 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 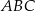 , w którym
, w którym 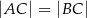 . Udowodnij, że
. Udowodnij, że  .
.
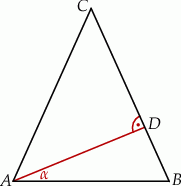
Wykaż, że miara kąta między wysokością trójkąta równoramiennego poprowadzoną do ramienia a podstawą tego trójkąta jest dwa razy mniejsza od miary kąta zawartego między ramionami tego trójkąta.
Na bokach 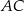 i
i 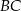 trójkąta
trójkąta 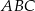 wybrano odpowiednio punkty
wybrano odpowiednio punkty 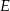 i
i 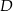 w ten sposób, że
w ten sposób, że 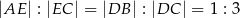 . Punkt
. Punkt 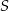 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 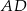 i
i 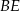 (zobacz rysunek).
(zobacz rysunek).
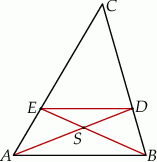
Oblicz pole trójkąta 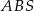 jeżeli pole trójkąta
jeżeli pole trójkąta 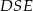 równe 36.
równe 36.
W trójkąt równoramienny 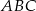 , w którym
, w którym 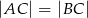 ,
, 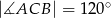 , wpisano okrąg, którego promień ma długość
, wpisano okrąg, którego promień ma długość  . Oblicz długości boków trójkąta.
. Oblicz długości boków trójkąta.
Dany jest trójkąt prostokątny o kącie ostrym 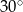 . Oblicz obwód tego trójkąta, jeżeli przeciwprostokątna ma długość 12 dm.
. Oblicz obwód tego trójkąta, jeżeli przeciwprostokątna ma długość 12 dm.
W trójkącie 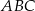 dane są długości boków:
dane są długości boków: 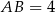 ,
, 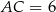 ,
, 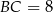 . Oblicz długości odcinków, na jakie dzieli bok
. Oblicz długości odcinków, na jakie dzieli bok 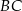 wysokość opuszczona z wierzchołka
wysokość opuszczona z wierzchołka 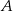 .
.
W trójkącie prostokątnym 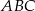 z wierzchołka kąta prostego poprowadzono odcinek
z wierzchołka kąta prostego poprowadzono odcinek 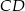 taki, że
taki, że 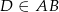 . Trójkąt
. Trójkąt 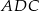 jest równoboczny. Oblicz pole trójkąta
jest równoboczny. Oblicz pole trójkąta 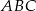 , wiedząc, że jego obwód jest równy 6.
, wiedząc, że jego obwód jest równy 6.
W trójkącie prostokątnym 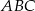 z wierzchołka kąta prostego poprowadzono odcinek
z wierzchołka kąta prostego poprowadzono odcinek 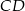 taki, że
taki, że 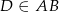 . Trójkąt
. Trójkąt 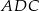 jest równoboczny. Oblicz pole trójkąta
jest równoboczny. Oblicz pole trójkąta 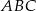 , wiedząc, że jego obwód jest równy 12.
, wiedząc, że jego obwód jest równy 12.
Na bokach 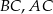 i
i 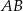 trójkąta
trójkąta 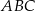 wybrano odpowiednio punkty
wybrano odpowiednio punkty 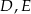 i
i 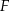 . Wykaż, że jeżeli okręgi opisane na trójkątach
. Wykaż, że jeżeli okręgi opisane na trójkątach 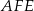 i
i 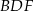 są styczne, to punkt
są styczne, to punkt 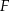 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 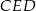 .
.
Punkt 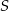 jest środkiem okręgu opisanego na trójkącie ostrokątnym
jest środkiem okręgu opisanego na trójkącie ostrokątnym 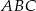 . Kąt
. Kąt 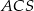 jest trzy razy większy od kąta
jest trzy razy większy od kąta 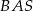 , a kąt
, a kąt 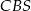 jest dwa razy większy od kąta
jest dwa razy większy od kąta 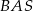 . Oblicz kąty trójkąta
. Oblicz kąty trójkąta 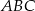 .
.
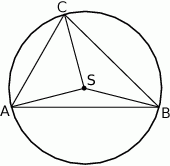
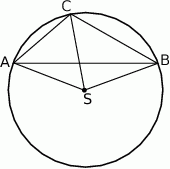
Punkt 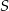 jest środkiem okręgu opisanego na trójkącie rozwartokątnym
jest środkiem okręgu opisanego na trójkącie rozwartokątnym 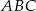 . Kąt
. Kąt 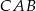 jest dwa razy większy od kąta
jest dwa razy większy od kąta 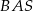 , a kąt
, a kąt 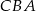 jest o
jest o 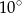 większy od kąta
większy od kąta 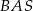 . Oblicz kąty trójkąta
. Oblicz kąty trójkąta 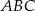 .
.
W trójkącie równobocznym bok jest o 6 cm dłuższy od wysokości trójkąta. Oblicz pole i obwód tego trójkąta.
W trójkącie równobocznym wysokość jest o 3 cm krótsza od boku trójkąta. Oblicz pole i obwód tego trójkąta.
Miara kąta między ramionami trójkąta równoramiennego o polu 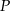 jest równa
jest równa  . Oblicz promień okręgu wpisanego w ten trójkąt.
. Oblicz promień okręgu wpisanego w ten trójkąt.
Znaleźć pole kwadratu wpisanego w trójkąt równoboczny o boku 4. Jakie pole ma koło opisane na tym kwadracie?
W trójkącie równoramiennym 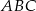 o podstawie
o podstawie 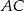 dane są:
dane są: 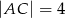 oraz
oraz 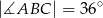 . Odcinek
. Odcinek 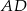 jest odcinkiem dwusiecznej kąta
jest odcinkiem dwusiecznej kąta 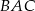 (zobacz rysunek).
(zobacz rysunek).
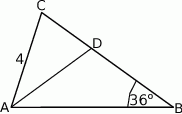
Oblicz długość odcinka 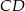 .
.
W trójkącie 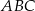 , w którym
, w którym 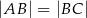 połączono wierzchołek
połączono wierzchołek 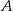 punktem
punktem 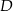 na boku
na boku 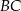 w ten sposób, że
w ten sposób, że 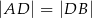 . Wyznacz miary kątów trójkąta
. Wyznacz miary kątów trójkąta 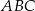 jeżeli
jeżeli 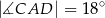 .
.
Bok 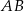 trójkąta
trójkąta 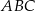 jest średnicą okręgu opisanego na tym trójkącie. Bok
jest średnicą okręgu opisanego na tym trójkącie. Bok 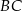 jest o 4 cm krótszy od boku
jest o 4 cm krótszy od boku 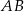 oraz
oraz 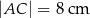 . Oblicz pole trójkąta
. Oblicz pole trójkąta 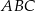 oraz długość promienia okręgu wpisanego w ten trójkąt.
oraz długość promienia okręgu wpisanego w ten trójkąt.
Bok 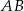 trójkąta
trójkąta 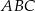 jest średnicą okręgu opisanego na tym trójkącie. Bok
jest średnicą okręgu opisanego na tym trójkącie. Bok 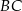 jest o 2 cm krótszy od boku
jest o 2 cm krótszy od boku 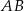 oraz
oraz 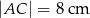 . Oblicz pole trójkąta
. Oblicz pole trójkąta 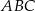 oraz długość promienia okręgu wpisanego w ten trójkąt.
oraz długość promienia okręgu wpisanego w ten trójkąt.

