Bok 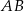 trójkąta
trójkąta 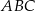 jest średnicą okręgu opisanego na tym trójkącie. Bok
jest średnicą okręgu opisanego na tym trójkącie. Bok 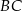 jest o 4 cm krótszy od boku
jest o 4 cm krótszy od boku 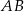 oraz
oraz 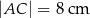 . Oblicz pole trójkąta
. Oblicz pole trójkąta 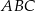 oraz długość promienia okręgu wpisanego w ten trójkąt.
oraz długość promienia okręgu wpisanego w ten trójkąt.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
Bok 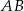 trójkąta
trójkąta 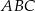 jest średnicą okręgu opisanego na tym trójkącie. Bok
jest średnicą okręgu opisanego na tym trójkącie. Bok 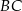 jest o 2 cm krótszy od boku
jest o 2 cm krótszy od boku 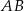 oraz
oraz 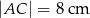 . Oblicz pole trójkąta
. Oblicz pole trójkąta 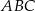 oraz długość promienia okręgu wpisanego w ten trójkąt.
oraz długość promienia okręgu wpisanego w ten trójkąt.
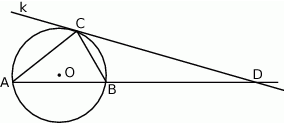
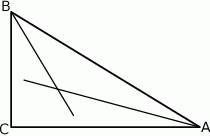
Na trójkącie 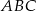 , w którym
, w którym 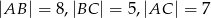 opisano okrąg o środku
opisano okrąg o środku 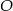 . Następnie poprowadzono styczną
. Następnie poprowadzono styczną 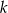 do okręgu w punkcie
do okręgu w punkcie 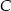 , która w punkcie
, która w punkcie 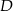 przecięła prostą zawierającą bok
przecięła prostą zawierającą bok 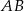 (jak na rysunku poniżej). Oblicz odległość punktu
(jak na rysunku poniżej). Oblicz odległość punktu 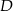 od wierzchołka
od wierzchołka 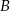 , jeżeli wiadomo, że
, jeżeli wiadomo, że 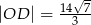 .
.
Podstawą trójkąta równobocznego jest średnica koła. Oblicz stosunek pola części trójkąta leżącej na zewnątrz koła do pola części trójkąta leżącej wewnątrz koła.
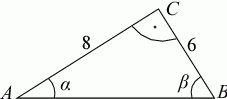
W trójkącie  dane są:
dane są: 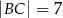 ,
, 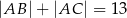 ,
, 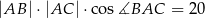 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
Na bokach 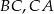 i
i 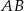 trójkąta
trójkąta 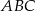 wybrano punkty
wybrano punkty 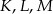 takie, że
takie, że
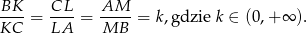
Oblicz stosunek pola trójkąta 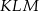 do pola trójkąta
do pola trójkąta 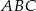 .
.
Suma długości wszystkich wysokości trójkąta 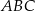 jest 9 razy większa od promienia okręgu wpisanego w ten trójkąt. Udowodnij, że trójkąt
jest 9 razy większa od promienia okręgu wpisanego w ten trójkąt. Udowodnij, że trójkąt 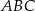 jest równoboczny.
jest równoboczny.
Wyznacz promień okręgu wpisanego w trójkąt równoramienny o ramieniu długości 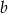 i kącie o mierze
i kącie o mierze  przy podstawie.
przy podstawie.
Na bokach 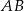 i
i 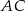 trójkąta
trójkąta 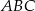 , który nie jest równoramienny, wybrano takie punkty
, który nie jest równoramienny, wybrano takie punkty 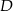 i
i 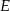 , że
, że 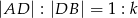 oraz
oraz 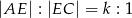 , dla
, dla 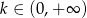 .
.
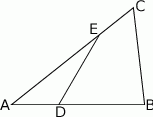
- Wyznacz wzór funkcji
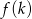 , która jest zdefiniowana jako stosunek pól trójkątów
, która jest zdefiniowana jako stosunek pól trójkątów 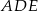 i
i 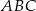 .
. - Wiedząc że
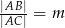 , dla
, dla 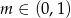 wyznacz wszystkie wartości parametru
wyznacz wszystkie wartości parametru 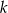 , dla których trójkąty
, dla których trójkąty 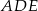 i
i 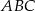 są podobne.
są podobne.
W trójkącie prostokątnym 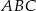 przyprostokątne mają długości
przyprostokątne mają długości 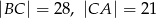 . Na boku
. Na boku 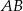 wybrano punkt
wybrano punkt 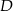 tak, że pole trójkąta
tak, że pole trójkąta 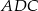 jest równe 126. Oblicz długość promienia okręgu opisanego na trójkącie
jest równe 126. Oblicz długość promienia okręgu opisanego na trójkącie 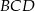 .
.
Uzasadnij, że jeżeli dwie dwusieczne trójkąta przecinają się pod kątem 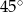 to trójkąt jest prostokątny.
to trójkąt jest prostokątny.
Punkt 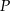 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 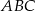 oraz
oraz 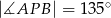 . Wykaż, że trójkąt
. Wykaż, że trójkąt 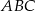 jest prostokątny.
jest prostokątny.
Korzystając z danych przedstawionych na rysunku, oblicz wartość wyrażenia:
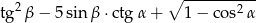
Na boku  trójkąta równobocznego
trójkąta równobocznego 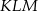 obrano taki punkt
obrano taki punkt 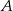 , że
, że 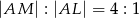 .
.
- Oblicz stosunek pól trójkątów
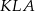 i
i 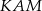 .
. - Oblicz stosunek promieni okręgów opisanych na tych trójkątach.
- Wyznacz
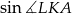 .
.
Dany jest trójkąt 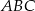 gdzie
gdzie 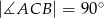 .
.
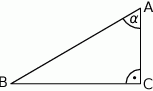
Wiadomo, że 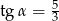 . Podaj wartości pozostałych funkcji trygonometrycznych kąta
. Podaj wartości pozostałych funkcji trygonometrycznych kąta  .
.
Dany jest trójkąt 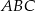 gdzie
gdzie 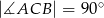 .
.
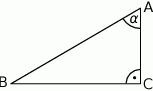
Wiadomo, że 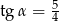 . Podaj wartości pozostałych funkcji trygonometrycznych kąta
. Podaj wartości pozostałych funkcji trygonometrycznych kąta  .
.
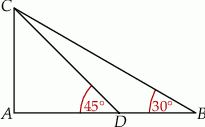
W trójkącie prostokątnym 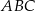 , w którym
, w którym 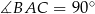 i
i 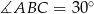 , wybrano na przyprostokątnej
, wybrano na przyprostokątnej 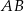 punkt
punkt 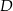 tak, że
tak, że 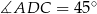 . Oblicz stosunek długości odcinków
. Oblicz stosunek długości odcinków 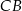 i
i 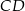 .
.
Wykaż, że jeżeli długości boków 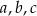 trójkąta prostokątnego są liczbami całkowitymi, to liczba
trójkąta prostokątnego są liczbami całkowitymi, to liczba 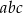 jest parzysta.
jest parzysta.
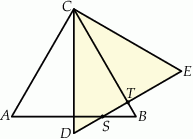
Trójkąty 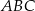 i
i 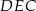 są przystającymi trójkątami równobocznymi o boku długości 6. Odcinki
są przystającymi trójkątami równobocznymi o boku długości 6. Odcinki 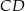 i
i 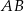 są prostopadłe, a odcinek
są prostopadłe, a odcinek 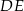 przecina odcinki
przecina odcinki 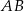 i
i 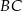 w punktach
w punktach 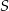 i
i 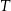 odpowiednio (zobacz rysunek). Oblicz długość odcinka
odpowiednio (zobacz rysunek). Oblicz długość odcinka 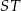 .
.
Dany jest trójkąt prostokątny, w którym  ,
, 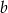 oznaczają długości przyprostokątnych,
oznaczają długości przyprostokątnych,  jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej
jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej  . Wiadomo, że
. Wiadomo, że 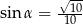 . Oblicz
. Oblicz
- tangens kąta
 ;
; - wartość wyrażenia
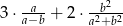 .
.
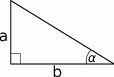
Uzasadnij, że kąt ostry między dwusiecznymi kątów ostrych trójkąta prostokątnego jest równy 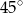 .
.
Liczby 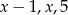 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Dwa boki trójkąta wpisanego w okrąg o promieniu 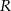 są odpowiednio równe
są odpowiednio równe 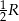 i
i 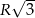 . Oblicz długość trzeciego boku.
. Oblicz długość trzeciego boku.

