Rozpatrujemy wszystkie trapezy 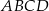 , których wierzchołki
, których wierzchołki 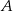 i
i 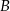 leżą na wykresie funkcji
leżą na wykresie funkcji 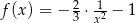 określonej dla
określonej dla 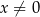 . Punkt
. Punkt 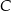 ma współrzędne
ma współrzędne 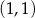 , a oś
, a oś 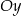 jest osią symetrii tego trapezu (zobacz rysunek).
jest osią symetrii tego trapezu (zobacz rysunek).
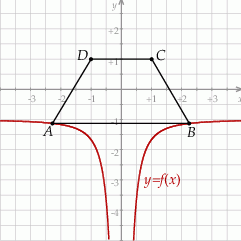
Oblicz obwód tego trapezu 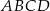 , którego pole jest najmniejsze możliwe.
, którego pole jest najmniejsze możliwe.

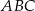 , w których
, w których 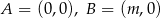 , gdzie
, gdzie 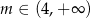 , a wierzchołek
, a wierzchołek 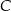 leży na prostej o równaniu
leży na prostej o równaniu 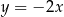 . Na boku
. Na boku 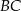 tego trójkąta leży punkt
tego trójkąta leży punkt 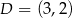 .
. 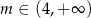 pole
pole 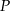 trójkąta
trójkąta 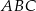 , jako funkcja zmiennej
, jako funkcja zmiennej 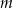 , wyraża się wzorem
, wyraża się wzorem 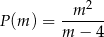
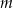 , dla której funkcja
, dla której funkcja 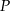 osiąga wartość najmniejszą. Wyznacz równanie prostej
osiąga wartość najmniejszą. Wyznacz równanie prostej 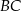 , przy której funkcja
, przy której funkcja 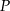 osiąga tę najmniejszą wartość.
osiąga tę najmniejszą wartość.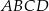 , których wierzchołki
, których wierzchołki 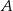 i
i 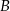 leżą na wykresie funkcji
leżą na wykresie funkcji 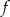 określonej wzorem
określonej wzorem 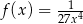 dla
dla 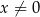 . Punkty
. Punkty 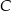 i
i 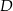 leżą na wykresie funkcji
leżą na wykresie funkcji 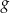 określonej wzorem
określonej wzorem 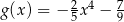 i są położone symetrycznie względem osi
i są położone symetrycznie względem osi 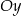 (zobacz rysunek). Oblicz współrzędne wierzchołka
(zobacz rysunek). Oblicz współrzędne wierzchołka 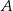 , dla którego pole prostokąta
, dla którego pole prostokąta 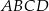 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole. 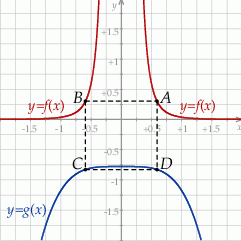
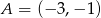 i
i 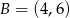 . Na wykresie funkcji
. Na wykresie funkcji 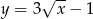 znajdź taki punkt
znajdź taki punkt 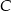 , dla którego pole trójkąta
, dla którego pole trójkąta 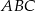 jest najmniejsze.
jest najmniejsze. 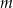 , dla której pole koła stycznego do prostych zawierających boki
, dla której pole koła stycznego do prostych zawierających boki 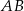 i
i 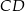 równoległoboku
równoległoboku 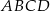 o wierzchołkach
o wierzchołkach 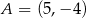 ,
, 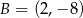 ,
, 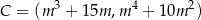 jest najmniejsze możliwe. Oblicz to pole.
jest najmniejsze możliwe. Oblicz to pole. 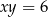 obrano punkty
obrano punkty 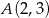 i
i 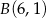 . Znajdź na tej krzywej taki punkt
. Znajdź na tej krzywej taki punkt 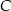 o ujemnej odciętej, aby pole trójkąta
o ujemnej odciętej, aby pole trójkąta 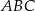 było najmniejsze.
było najmniejsze. 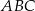 , których wierzchołki
, których wierzchołki 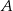 i
i 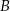 leżą na wykresie funkcji
leżą na wykresie funkcji 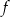 określonej wzorem
określonej wzorem 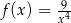 dla
dla 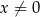 . Punkt
. Punkt 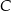 ma współrzędne
ma współrzędne 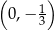 , a punkty
, a punkty 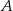 i
i 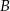 , są położone symetrycznie względem osi
, są położone symetrycznie względem osi 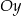 (zobacz rysunek). Oblicz współrzędne wierzchołków
(zobacz rysunek). Oblicz współrzędne wierzchołków 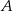 i
i 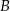 , dla których pole trójkąta
, dla których pole trójkąta 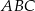 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole. 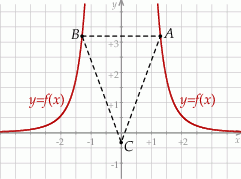
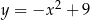 . Na tej paraboli leży punkt
. Na tej paraboli leży punkt 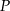 o dodatnich współrzędnych. Wyznacz współrzędne tego punktu tak, by styczna do paraboli w punkcie
o dodatnich współrzędnych. Wyznacz współrzędne tego punktu tak, by styczna do paraboli w punkcie 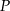 ograniczała wraz z osiami układu współrzędnych trójkąt o najmniejszym polu.
ograniczała wraz z osiami układu współrzędnych trójkąt o najmniejszym polu. 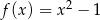 określona dla
określona dla 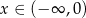 . W jakim punkcie wykresu tej funkcji należy poprowadzić styczną tak, aby trójkąt ograniczony tą styczną i osiami układu współrzędnych miał najmniejsze pole? Oblicz to pole.
. W jakim punkcie wykresu tej funkcji należy poprowadzić styczną tak, aby trójkąt ograniczony tą styczną i osiami układu współrzędnych miał najmniejsze pole? Oblicz to pole. 