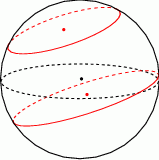
Kulę o promieniu 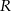 przecięto dwiema równoległymi płaszczyznami w sposób przedstawiony na poniższym rysunku. Przekroje mają promienie
przecięto dwiema równoległymi płaszczyznami w sposób przedstawiony na poniższym rysunku. Przekroje mają promienie 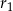 oraz
oraz 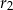 i są odległe od siebie o
i są odległe od siebie o  . Liczby
. Liczby 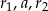 w podanej kolejności tworzą trzywyrazowy ciąg arytmetyczny, którego różnica jest równa 1. Suma wyrazów tego ciągu jest równa 18. Znajdź długość promienia kuli.
w podanej kolejności tworzą trzywyrazowy ciąg arytmetyczny, którego różnica jest równa 1. Suma wyrazów tego ciągu jest równa 18. Znajdź długość promienia kuli.

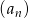 jest ciągiem arytmetycznym, w którym
jest ciągiem arytmetycznym, w którym 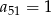 oraz wyrażanie
oraz wyrażanie 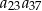 ma najmniejszą możliwą wartość. Wyznacz
ma najmniejszą możliwą wartość. Wyznacz 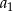 .
.  , dla których istnieje suma nieskończonego ciągu geometrycznego
, dla których istnieje suma nieskończonego ciągu geometrycznego 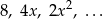
 i
i 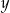 liczby
liczby 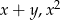 oraz
oraz 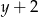 są trzema kolejnymi wyrazami zarówno ciągu arytmetycznego, jak i geometrycznego?
są trzema kolejnymi wyrazami zarówno ciągu arytmetycznego, jak i geometrycznego?  i
i 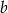 liczby
liczby 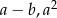 oraz
oraz 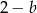 są trzema kolejnymi wyrazami zarówno ciągu arytmetycznego, jak i geometrycznego?
są trzema kolejnymi wyrazami zarówno ciągu arytmetycznego, jak i geometrycznego? 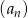 określony dla
określony dla 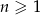 , w którym iloraz jest równy pierwszemu wyrazowi, a suma wszystkich wyrazów tego ciągu jest równa 12. Oblicz pierwszy wyraz tego ciągu.
, w którym iloraz jest równy pierwszemu wyrazowi, a suma wszystkich wyrazów tego ciągu jest równa 12. Oblicz pierwszy wyraz tego ciągu. 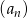 określony dla
określony dla 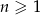 , w którym iloraz jest dwa razy większy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa 14. Oblicz pierwszy wyraz tego ciągu.
, w którym iloraz jest dwa razy większy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa 14. Oblicz pierwszy wyraz tego ciągu.  oraz
oraz 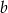 , dla których ciąg
, dla których ciąg 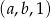 jest ciągiem arytmetycznym, natomiast ciąg
jest ciągiem arytmetycznym, natomiast ciąg 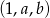 jest ciągiem geometrycznym.
jest ciągiem geometrycznym. 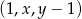 jest arytmetyczny, natomiast ciąg
jest arytmetyczny, natomiast ciąg 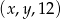 jest geometryczny. Oblicz
jest geometryczny. Oblicz  oraz
oraz 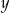 i podaj ten ciąg geometryczny.
i podaj ten ciąg geometryczny. 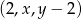 jest arytmetyczny, natomiast ciąg
jest arytmetyczny, natomiast ciąg 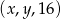 jest geometryczny. Oblicz
jest geometryczny. Oblicz  oraz
oraz 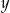 i podaj ten ciąg geometryczny.
i podaj ten ciąg geometryczny. 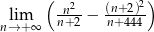 .
. 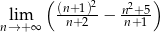 .
. 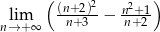 .
. 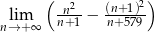 .
. 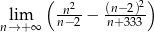 .
. 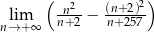 .
. 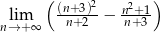 .
. 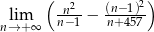 .
. 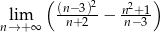 .
. 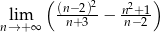 .
.  tworzą ciąg geometryczny o ilorazie
tworzą ciąg geometryczny o ilorazie  . Wyznacz pierwszy z tych logarytmów jeśli jest on mniejszy od -1 oraz suma dwóch pierwszych logarytmów jest równa sumie dwóch pozostałych
. Wyznacz pierwszy z tych logarytmów jeśli jest on mniejszy od -1 oraz suma dwóch pierwszych logarytmów jest równa sumie dwóch pozostałych  ,
, 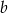 ,
,  (w podanej kolejności) tworzą ciąg arytmetyczny. Wyraź w procentach jaką część wysokości trójkąta poprowadzonej na bok długości
(w podanej kolejności) tworzą ciąg arytmetyczny. Wyraź w procentach jaką część wysokości trójkąta poprowadzonej na bok długości 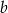 stanowi promień okręgu wpisanego w ten trójkąt.
stanowi promień okręgu wpisanego w ten trójkąt. 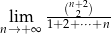 .
. 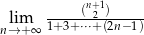 .
. 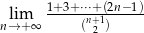 .
. 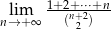 .
. 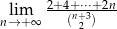 .
. 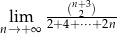 .
. 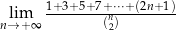 .
. 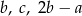 są kolejnymi wyrazami ciągu geometrycznego to liczby
są kolejnymi wyrazami ciągu geometrycznego to liczby 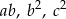 są kolejnymi wyrazami ciągu arytmetycznego.
są kolejnymi wyrazami ciągu arytmetycznego. 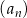 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 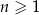 . Ilorazem tego ciągu jest liczba
. Ilorazem tego ciągu jest liczba 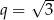 , a iloczyn 5 początkowych wyrazów tego ciągu:
, a iloczyn 5 początkowych wyrazów tego ciągu: 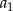 ,
, 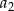 ,
, 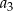 ,
, 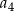 ,
, 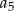 jest równy
jest równy 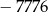 .
. 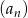 , w którym
, w którym 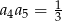 oraz
oraz 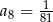 .
. 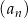 określonego dla
określonego dla 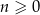 jest równa
jest równa 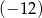 . Ponadto dla każdej liczby całkowitej
. Ponadto dla każdej liczby całkowitej 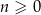 spełniony jest warunek
spełniony jest warunek 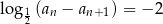 . Oblicz nieskończoną sumę
. Oblicz nieskończoną sumę 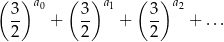
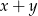 ,
, 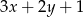 i
i 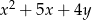 tworzą ciąg arytmetyczny. Wyznacz te wartości
tworzą ciąg arytmetyczny. Wyznacz te wartości  , dla których ciąg ten jest rosnący.
, dla których ciąg ten jest rosnący. 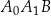 kąt
kąt 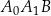 jest prosty,
jest prosty, 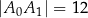 i
i 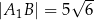 . Odcinek
. Odcinek 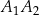 jest wysokością tego trójkąta, odcinek
jest wysokością tego trójkąta, odcinek 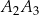 jest wysokością trójkąta
jest wysokością trójkąta 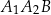 , odcinek
, odcinek 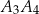 jest wysokością trójkąta
jest wysokością trójkąta 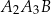 itd. Ogólnie, dla każdej liczby naturalnej
itd. Ogólnie, dla każdej liczby naturalnej 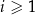 , odcinek
, odcinek 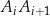 jest wysokością trójkąta
jest wysokością trójkąta 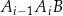
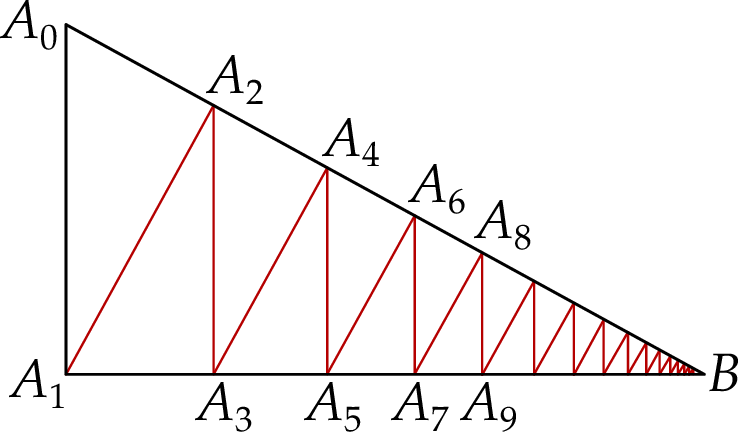
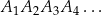 .
. 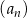 , dla
, dla 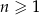 suma wyrazów trzeciego, czwartego i piątego wynosi 144. Oblicz sumę siedmiu początkowych wyrazów ciągu
suma wyrazów trzeciego, czwartego i piątego wynosi 144. Oblicz sumę siedmiu początkowych wyrazów ciągu 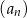 .
. 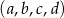 ma wszystkie wyrazy ujemne i jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 2. Oblicz iloczyn
ma wszystkie wyrazy ujemne i jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 2. Oblicz iloczyn 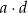 .
. 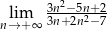 .
. 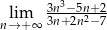 .
. 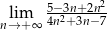 .
. 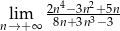 .
. 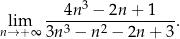
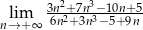 .
. 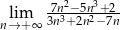 .
. 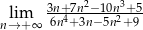 .
. 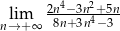 .
. 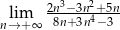 .
. 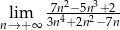 .
. 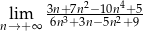 .
. 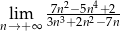 .
. 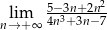 .
. 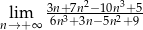 .
. 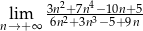 .
. 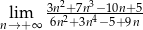 .
. 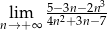 .
. 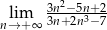 .
. 