Oblicz pierwszy wyraz i iloraz ciągu geometrycznego 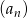 , wiedząc, że
, wiedząc, że 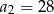 i
i 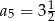 . Oblicz sumę dziesięciu początkowych wyrazów tego ciągu.
. Oblicz sumę dziesięciu początkowych wyrazów tego ciągu.
/Szkoła średnia/Ciągi
Trzy liczby całkowite tworzą ciąg geometryczny o ilorazie będącym ujemną liczbą całkowitą. Jeżeli najmniejszą z tych liczb zwiększymy o 9, to liczby te (w tej samej kolejności) są kolejnymi wyrazami ciągu arytmetycznego. Wyznacz te liczby.
Trzy różne liczby całkowite tworzą ciąg geometryczny o ilorazie będącym ujemną liczbą całkowitą. Jeżeli najmniejszą z tych liczb zwiększymy o 16, to liczby te (w tej samej kolejności) są kolejnymi wyrazami ciągu arytmetycznego. Wyznacz te liczby.
Długości boków trójkąta są kolejnymi wyrazami ciągu arytmetycznego. Obwód trójkąta jest równy 21, a cosinus największego kąta jest równy 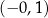 . Oblicz długości boków tego trójkąta.
. Oblicz długości boków tego trójkąta.
Ciąg 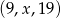 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 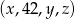 jest geometryczny. Oblicz
jest geometryczny. Oblicz 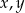 oraz
oraz  .
.
Ciąg 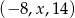 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 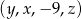 jest geometryczny. Oblicz
jest geometryczny. Oblicz 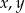 oraz
oraz  .
.
Ciąg 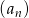 określony jest wzorem
określony jest wzorem 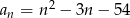 .
.
- Nie korzystając z kalkulatora, rozstrzygnij, czy 58 wyraz ciągu
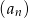 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej. - Znajdź takie dwa kolejne wyrazy ciągu
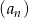 , aby ich rożnica była równa 20.
, aby ich rożnica była równa 20.
Dany jest ciąg arytmetyczny 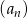 określony dla każdej liczby naturalnej
określony dla każdej liczby naturalnej 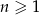 , w którym
, w którym 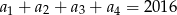 oraz
oraz 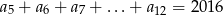 . Oblicz pierwszy wyraz, różnicę oraz najmniejszy dodatni wyraz ciągu
. Oblicz pierwszy wyraz, różnicę oraz najmniejszy dodatni wyraz ciągu 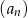 .
.
Dany jest ciąg arytmetyczny 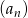 określony dla każdej liczby naturalnej
określony dla każdej liczby naturalnej 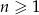 , w którym
, w którym 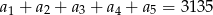 oraz
oraz 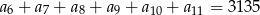 . Oblicz pierwszy wyraz, różnicę oraz najmniejszy dodatni wyraz ciągu
. Oblicz pierwszy wyraz, różnicę oraz najmniejszy dodatni wyraz ciągu 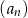 .
.
Suma nieskończonego zbieżnego ciągu geometrycznego jest równa 56, a suma kwadratów wyrazów tego ciągu jest równa 448. Znajdź pierwszy wyraz tego ciągu i napisz wzór na wyraz ogólny.
Oblicz granicę 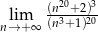 .
.
Oblicz granicę 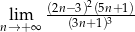 .
.
Oblicz granicę 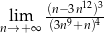 .
.
Oblicz granicę 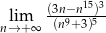 .
.
Oblicz granicę 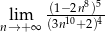 .
.
Oblicz granicę 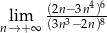 .
.
Oblicz granicę 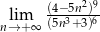 .
.
Oblicz granicę 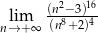 .
.
Oblicz granicę 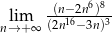 .
.
Oblicz granicę ciągu 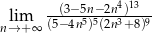 .
.
Oblicz granicę 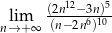 .
.
Ciąg 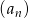 jest ciągiem arytmetycznym o pierwszym wyrazie równym 123 i różnicy będącej liczbą całkowitą. Ciąg
jest ciągiem arytmetycznym o pierwszym wyrazie równym 123 i różnicy będącej liczbą całkowitą. Ciąg 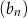 jest określony wzorem
jest określony wzorem 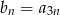 , dla
, dla 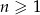 , oraz wiadomo, że suma pewnych
, oraz wiadomo, że suma pewnych 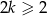 początkowych wyrazów ciągu
początkowych wyrazów ciągu 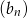 jest równa sumie
jest równa sumie 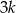 początkowych wyrazów ciągu
początkowych wyrazów ciągu 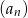 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 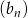 .
.
Wyznacz wzór na  -ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 10, a wyrazy trzeci, piąty i trzynasty tworzą w podanej kolejności ciąg geometryczny.
-ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 10, a wyrazy trzeci, piąty i trzynasty tworzą w podanej kolejności ciąg geometryczny.
Wyznacz wzór na  -ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 40, a wyrazy drugi, piąty i dwudziesty trzeci tworzą w podanej kolejności ciąg geometryczny.
-ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 40, a wyrazy drugi, piąty i dwudziesty trzeci tworzą w podanej kolejności ciąg geometryczny.
Rosnący ciąg arytmetyczny 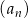 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 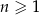 . Suma pierwszych pięciu wyrazów tego ciągu jest równa 10. Wyrazy
. Suma pierwszych pięciu wyrazów tego ciągu jest równa 10. Wyrazy 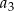 ,
, 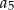 ,
, 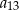 tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na
tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na  –ty wyraz ciągu arytmetycznego
–ty wyraz ciągu arytmetycznego 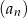 .
.
Rosnący ciąg arytmetyczny 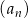 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 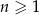 . Suma pierwszych dwunastu wyrazów tego ciągu jest równa 240. Wyrazy
. Suma pierwszych dwunastu wyrazów tego ciągu jest równa 240. Wyrazy 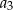 ,
, 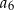 ,
, 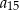 tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na
tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na  –ty wyraz ciągu arytmetycznego
–ty wyraz ciągu arytmetycznego  .
.
Ciąg 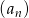 określony jest w taki sposób:
określony jest w taki sposób: 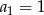 , zaś
, zaś  -ty wyraz ciągu
-ty wyraz ciągu 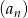 , gdy
, gdy 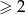 , jest największym dzielnikiem liczby
, jest największym dzielnikiem liczby  mniejszym od
mniejszym od  . Ile wyrazów ciągu
. Ile wyrazów ciągu 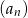 jest równych 2? Odpowiedź uzasadnij.
jest równych 2? Odpowiedź uzasadnij.
Liczby 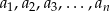 są kolejnymi wyrazami ciągu geometrycznego o dodatnich wyrazach, a
są kolejnymi wyrazami ciągu geometrycznego o dodatnich wyrazach, a  jest liczbą parzystą. Znając sumy
jest liczbą parzystą. Znając sumy
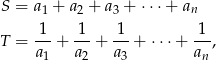
oblicz iloczyn 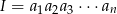 .
.
Trzynasty wyraz ciągu geometrycznego jest równy 10. Oblicz wartość iloczynu dwudziestu pięciu początkowych wyrazów tego ciągu.
Oblicz 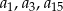 oraz sumę
oraz sumę 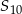 dziesięciu pierwszych wyrazów ciągu arytmetycznego
dziesięciu pierwszych wyrazów ciągu arytmetycznego 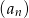 jeżeli
jeżeli 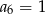 i
i 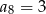 .
.
Oblicz 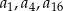 oraz sumę
oraz sumę 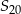 dwudziestu pierwszych wyrazów ciągu arytmetycznego
dwudziestu pierwszych wyrazów ciągu arytmetycznego 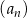 jeżeli
jeżeli 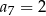 i
i 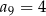 .
.
Oblicz 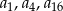 oraz sumę
oraz sumę 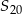 dwudziestu pierwszych wyrazów ciągu arytmetycznego
dwudziestu pierwszych wyrazów ciągu arytmetycznego 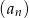 jeżeli
jeżeli 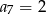 i
i 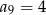 .
.
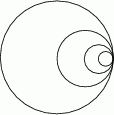
Dany jest okrąg 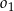 o promieniu
o promieniu  . Wewnątrz tego okręgu narysowano okrąg
. Wewnątrz tego okręgu narysowano okrąg 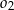 styczny wewnętrznie o średnicy
styczny wewnętrznie o średnicy  , wewnątrz okręgu
, wewnątrz okręgu 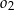 znów narysowano okrąg styczny wewnętrznie o średnicy
znów narysowano okrąg styczny wewnętrznie o średnicy 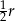 itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę długości wszystkich skonstruowanych w ten sposób okręgów.
itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę długości wszystkich skonstruowanych w ten sposób okręgów.
Sprawdź czy podane liczby
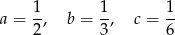
tworzą ciąg arytmetyczny (w podanej kolejności).
Dany jest nieskończony ciąg geometryczny 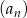 określony dla
określony dla 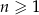 , w którym
, w którym 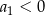 . Suma
. Suma 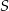 wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność
wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność 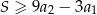 . Wykaż, ze
. Wykaż, ze 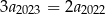 .
.
Ciągi 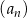 i
i 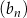 , gdzie
, gdzie 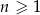 , są ciągami arytmetycznymi. Ciąg
, są ciągami arytmetycznymi. Ciąg 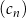 jest określony wzorem
jest określony wzorem 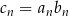 , dla
, dla 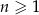 , a ciąg
, a ciąg 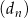 ciągiem różnic dwóch kolejnych wyrazów ciągu
ciągiem różnic dwóch kolejnych wyrazów ciągu 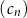 :
: 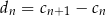 , dla
, dla 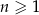 . Wykaż, że ciąg
. Wykaż, że ciąg 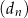 jest ciągiem arytmetycznym, którego różnica jest równa podwojonemu iloczynowi różnic ciągów
jest ciągiem arytmetycznym, którego różnica jest równa podwojonemu iloczynowi różnic ciągów 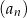 i
i 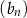 .
.
Wyraz ogólny ciągu 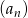 dany jest wzorem
dany jest wzorem 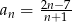 , gdzie
, gdzie 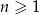 .
.
- Który wyraz ciągu
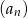 równa się
równa się 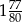 ?
? - Ile wyrazów danego ciągu należy do przedziału
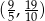 ?
? - Które wyrazy tego ciągu przyjmują wartości całkowite?
Liczby 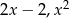 i
i 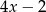 tworzą (w podanej kolejności) ciąg arytmetyczny i są trzema początkowymi wyrazami czterowyrazowego ciągu
tworzą (w podanej kolejności) ciąg arytmetyczny i są trzema początkowymi wyrazami czterowyrazowego ciągu 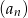 . Oblicz czwarty wyraz ciągu
. Oblicz czwarty wyraz ciągu 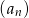 , wiedząc że liczby
, wiedząc że liczby 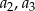 i
i 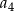 są trzema kolejnymi wyrazami pewnego ciągu geometrycznego.
są trzema kolejnymi wyrazami pewnego ciągu geometrycznego.

