W zbieżnym nieskończonym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy 4, a różnica między trzecim i piątym wyrazem jest równa 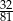 . Jaka jest suma wyrazów tego ciągu?
. Jaka jest suma wyrazów tego ciągu?
/Szkoła średnia/Ciągi
Ciąg arytmetyczny 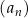 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 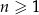 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy 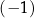 , a suma piętnastu początkowych kolejnych wyrazów tego ciągu jest równa
, a suma piętnastu początkowych kolejnych wyrazów tego ciągu jest równa 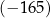 . Oblicz różnicę tego ciągu.
. Oblicz różnicę tego ciągu.
Udowodnić, że w dowolnym trójkącie prostokątnym, w którym długości boków tworzą ciąg arytmetyczny, promień okręgu wpisanego w ten trójkąt jest równy różnicy ciągu długości jego boków.
Udowodnij, że jeżeli liczby 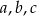 są kolejnymi wyrazami ciągu geometrycznego, to
są kolejnymi wyrazami ciągu geometrycznego, to

Ciąg 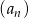 dla
dla 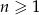 jest ciągiem arytmetycznym oraz
jest ciągiem arytmetycznym oraz 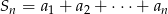 dla
dla 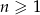 . Wykaż, że jeżeli spełniony jest warunek
. Wykaż, że jeżeli spełniony jest warunek 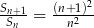 dla
dla 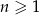 , to spełniony jest również warunek
, to spełniony jest również warunek 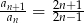 .
.
Oblicz granicę 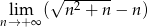 .
.
Oblicz granicę 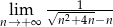 .
.
Oblicz granicę 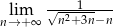 .
.
Oblicz granicę 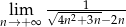 .
.
Oblicz granicę 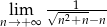 .
.
Oblicz granicę 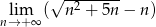 .
.
Oblicz granicę 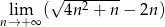 .
.
Oblicz granicę 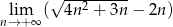 .
.
Oblicz granicę 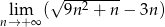 .
.
Oblicz granicę 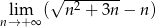 .
.
Oblicz granicę 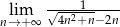 .
.
Oblicz granicę 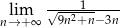 .
.
Oblicz granicę 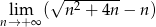 .
.
Iloraz ciągu geometrycznego 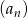 jest równy
jest równy 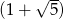 . Uzasadnij, że dla każdej liczby naturalnej
. Uzasadnij, że dla każdej liczby naturalnej 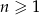 prawdziwy jest wzór
prawdziwy jest wzór 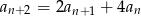 .
.
Ciąg 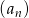 jest określony dla
jest określony dla 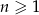 i spełnia warunki
i spełnia warunki
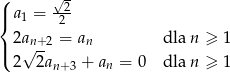
Oblicz granicę
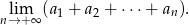
Wyznacz wszystkie wyrazy nieskończonego ciągu 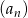 określonego wzorem
określonego wzorem 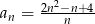 ,
, 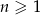 , które są liczbami całkowitymi.
, które są liczbami całkowitymi.
Liczby niezerowe 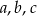 są wyrazami ciągu geometrycznego o numerach odpowiednio
są wyrazami ciągu geometrycznego o numerach odpowiednio 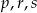 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
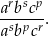
Ciąg 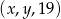 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 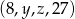 jest geometryczny. Oblicz
jest geometryczny. Oblicz 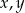 oraz
oraz  .
.
Sinus pewnego kąta ostrego  , liczba
, liczba  oraz cosinus tego samego kąta
oraz cosinus tego samego kąta  tworzą w podanej kolejności ciąg geometryczny. Oblicz sumę
tworzą w podanej kolejności ciąg geometryczny. Oblicz sumę 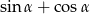 .
.
Średnia arytmetyczna  początkowych wyrazów ciągu
początkowych wyrazów ciągu 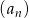 jest równa
jest równa 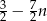 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 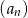 .
.
Średnia arytmetyczna  początkowych wyrazów ciągu
początkowych wyrazów ciągu 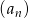 jest równa
jest równa 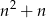 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 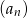 .
.
Ciąg 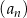 jest geometryczny o wyrazie pierwszym równym
jest geometryczny o wyrazie pierwszym równym 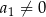 i ilorazie
i ilorazie 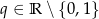 , Oblicz sumę
, Oblicz sumę 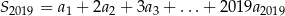 .
.
Różnica ciągu arytmetycznego 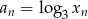 jest równa
jest równa 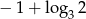 . Oblicz
. Oblicz 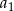 jeżeli wiadomo, że
jeżeli wiadomo, że
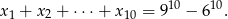
Oblicz granicę 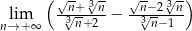 .
.
Iloraz ciągu geometrycznego 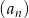 , gdzie
, gdzie 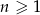 jest równy
jest równy 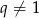 , a suma 10 początkowych wyrazów tego ciągu spełnia warunek
, a suma 10 początkowych wyrazów tego ciągu spełnia warunek 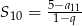 . Oblicz pierwszy wyraz tego ciągu.
. Oblicz pierwszy wyraz tego ciągu.
Oblicz granicę 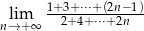 .
.
Oblicz granicę 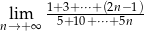 .
.
Oblicz granicę 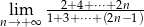 .
.
Oblicz granicę 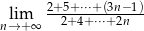 .
.
Oblicz granicę 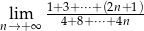 .
.
Oblicz granicę 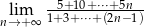 .
.
Oblicz granicę 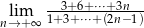 .
.
Oblicz granicę 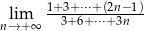 .
.
Oblicz granicę 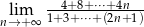 .
.
Oblicz granicę 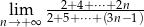 .
.
Oblicz granicę 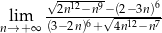 .
.
Dany jest ciąg 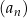 określony wzorem rekurencyjnym
określony wzorem rekurencyjnym
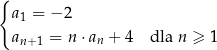
Oblicz sumę czterech początkowych wyrazów ciągu 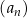 .
.

