Nieskończony ciąg liczbowy 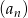 jest określony wzorem
jest określony wzorem 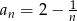 , dla
, dla 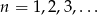 .
.
- Oblicz, ile wyrazów ciągu
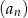 jest mniejszych od 1,975.
jest mniejszych od 1,975. - Dla pewnej liczby
 trzywyrazowy ciąg
trzywyrazowy ciąg 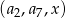 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz  .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Nieskończony ciąg liczbowy 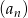 jest określony wzorem
jest określony wzorem 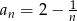 , dla
, dla 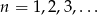 .
.
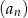 jest mniejszych od 1,975.
jest mniejszych od 1,975.  trzywyrazowy ciąg
trzywyrazowy ciąg 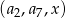 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz  .
.Ciąg 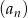 jest określony wzorem
jest określony wzorem 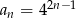 , gdzie
, gdzie 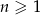 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 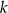 , dla których iloczyn
, dla których iloczyn 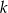 początkowych wyrazów ciągu
początkowych wyrazów ciągu 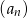 jest równy
jest równy 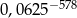 .
.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 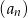 wynosi 124, a suma wszystkich wyrazów tego ciągu równa się 125.
wynosi 124, a suma wszystkich wyrazów tego ciągu równa się 125.
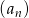 .
.  , dla którego
, dla którego ![2√2[(1+ √2)2−3] an = 5(√3+-1)(√-3−-1)](https://img.zadania.info/zad/7172985/HzadT3x.gif) .
.  i
i 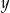 należy wstawić między pierwszy i trzeci wyraz ciągu
należy wstawić między pierwszy i trzeci wyraz ciągu 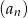 , aby ciąg
, aby ciąg 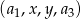 był ciągiem arytmetycznym?
był ciągiem arytmetycznym?Ciągi 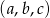 i
i 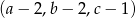 są ciągami geometrycznymi o wyrazach dodatnich, a ciąg
są ciągami geometrycznymi o wyrazach dodatnich, a ciąg 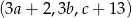 jest ciągiem arytmetycznym. Wyznacz
jest ciągiem arytmetycznym. Wyznacz 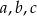 .
.
Trzy liczby tworzą ciąg geometryczny. Jeżeli do drugiej liczby dodamy 8, to ciąg ten zmieni się w arytmetyczny. Jeżeli zaś do ostatniej liczby nowego ciągu arytmetycznego dodamy 64, to tak otrzymany ciąg będzie znów geometryczny. Znajdź te liczby. Uwzględnij wszystkie możliwości.
Wyznacz pierwszy wyraz oraz różnicę ciągu arytmetycznego, jeżeli suma wyrazów pierwszego i siódmego jest równa 2, natomiast suma wyrazów trzeciego i szóstego jest równa 1.
Wyznacz pierwszy wyraz oraz różnicę ciągu arytmetycznego, jeżeli suma wyrazów drugiego i trzeciego jest równa -4, natomiast różnica wyrazów szóstego i dziesiątego jest równa 8.
Suma drugiego i trzeciego wyrazu ciągu arytmetycznego  jest równa 0, a różnica trzeciego i czwartego wyrazu tego ciągu jest równa
jest równa 0, a różnica trzeciego i czwartego wyrazu tego ciągu jest równa 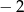 . Wyznacz różnicę tego ciągu i jego pierwszy wyraz.
. Wyznacz różnicę tego ciągu i jego pierwszy wyraz.
W ciągu geometrycznym 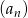 , którego żaden wyraz nie jest równy 0, suma pewnych dwóch kolejnych wyrazów jest równa 0. Oblicz sumę 2008 początkowych wyrazów tego ciągu.
, którego żaden wyraz nie jest równy 0, suma pewnych dwóch kolejnych wyrazów jest równa 0. Oblicz sumę 2008 początkowych wyrazów tego ciągu.
Długość krawędzi bocznej  prostopadłościennego pudełka o podstawie prostokąta tworzy wraz z długościami krawędzi podstawy
prostopadłościennego pudełka o podstawie prostokąta tworzy wraz z długościami krawędzi podstawy 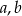 (w kolejności
(w kolejności 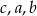 ) ciąg artymetyczny o różnicy -2.
) ciąg artymetyczny o różnicy -2.
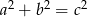 .
. Miary pięciu kątów tworzą ciąg arytmetyczny. Drugim wyrazem tego ciągu jest 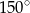 , a czwartym
, a czwartym 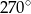 . Oblicz sumę sinusów tych pięciu kątów.
. Oblicz sumę sinusów tych pięciu kątów.
Ciąg arytmetyczny 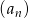 jest określony wzorem
jest określony wzorem 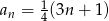 dla
dla 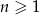 .
.
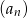 jest liczba
jest liczba 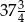 .
. 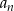 są wyrazy będące liczbami całkowitymi. Oblicz sumę wszystkich tych wyrazów.
są wyrazy będące liczbami całkowitymi. Oblicz sumę wszystkich tych wyrazów.Pierwiastkami wielomianu czwartego stopnia 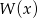 są liczby
są liczby 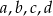 , które w podanej kolejności tworzą ciąg arytmetyczny o różnicy 2. Suma pierwiastków równa jest 8.
, które w podanej kolejności tworzą ciąg arytmetyczny o różnicy 2. Suma pierwiastków równa jest 8.
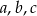 i
i 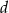 .
. 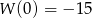 , przedstaw wielomian w postaci
, przedstaw wielomian w postaci 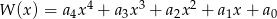 .
.Liczby 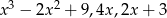 są kolejnymi wyrazami malejącego ciągu arytmetycznego. Oblicz
są kolejnymi wyrazami malejącego ciągu arytmetycznego. Oblicz  .
.
Pomiędzy liczby 243 i 48 wstaw takie trzy liczby, aby wraz z danymi tworzyły
Dany jest ciąg arytmetyczny 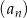 , określony dla
, określony dla 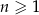 , w którym spełniona jest równość
, w którym spełniona jest równość 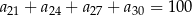 . Oblicz sumę
. Oblicz sumę 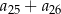 .
.
Dany jest ciąg arytmetyczny 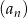 , określony dla
, określony dla 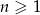 , w którym spełniona jest równość
, w którym spełniona jest równość 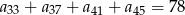 . Oblicz sumę
. Oblicz sumę 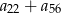 .
.
Dany jest nieskończony ciąg sześcianów 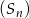 określony dla
określony dla 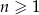 . Krawędź pierwszego z nich jest równa
. Krawędź pierwszego z nich jest równa 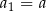 . Krawędź drugiego z tych sześcianów ma długość
. Krawędź drugiego z tych sześcianów ma długość 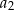 równą różnicy długości przekątnej i przekątnej ściany pierwszego sześcianu. Analogicznie, trzeci sześcian ma krawędź
równą różnicy długości przekątnej i przekątnej ściany pierwszego sześcianu. Analogicznie, trzeci sześcian ma krawędź 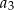 o długości równej różnicy długości przekątnej i przekątnej ściany drugiego sześcianu, itd. Oblicz sumę pól powierzchni wszystkich sześcianów tworzących ciąg
o długości równej różnicy długości przekątnej i przekątnej ściany drugiego sześcianu, itd. Oblicz sumę pól powierzchni wszystkich sześcianów tworzących ciąg 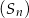 .
.
Ciąg arytmetyczny 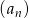 określony jest wzorem
określony jest wzorem 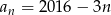 , dla
, dla 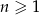 . Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
Ciąg arytmetyczny 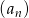 określony jest wzorem
określony jest wzorem 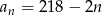 , dla
, dla 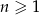 . Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
Wyrazami skończonego i malejącego ciągu 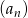 są wszystkie liczby trzycyfrowe podzielne przez 9.
są wszystkie liczby trzycyfrowe podzielne przez 9.
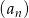 .
. 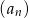 .
.Ciąg 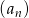 jest ciągiem arytmetycznym o różnicy 2, a ciąg
jest ciągiem arytmetycznym o różnicy 2, a ciąg 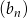 zdefiniowany jest wzorem
zdefiniowany jest wzorem 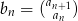 , dla
, dla 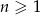 . Wyznacz wartość
. Wyznacz wartość  , dla której
, dla której 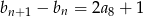 .
.
Wyrazy ciągu geometrycznego 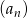 , w którym
, w którym 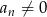 dla
dla 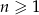 spełniają warunek
spełniają warunek
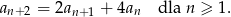
Wykaż, że wyrazy tego ciągu spełniają również warunek
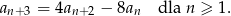
Udowodnij, że jeżeli liczby 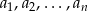 , gdzie
, gdzie 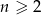 , tworzą ciąg arytmetyczny i żadna z nich nie jest zerem, to
, tworzą ciąg arytmetyczny i żadna z nich nie jest zerem, to
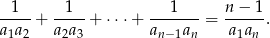
W zbieżnym nieskończonym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy 4, a różnica między trzecim i piątym wyrazem jest równa 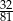 . Jaka jest suma wyrazów tego ciągu?
. Jaka jest suma wyrazów tego ciągu?
