Pierwszy wyraz ciągu arytmetycznego 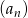 wynosi 1. Dla jakiej wartości różnicy
wynosi 1. Dla jakiej wartości różnicy  wyrażenie
wyrażenie 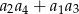 ma wartość najmniejszą i ile ona wynosi?
ma wartość najmniejszą i ile ona wynosi?
/Szkoła średnia/Ciągi
Pierwszy wyraz i iloraz nieskończonego ciągu geometrycznego malejącego 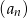 są różnymi pierwiastkami równania
są różnymi pierwiastkami równania 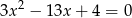 . Sprawdź czy prawdziwa jest nierówność
. Sprawdź czy prawdziwa jest nierówność 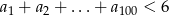 .
.
Oblicz granicę 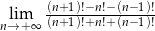 .
.
Dany jest ciąg arytmetyczny 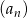 , gdzie
, gdzie 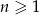 . Wiadomo, że dla każdego
. Wiadomo, że dla każdego 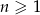 suma
suma  początkowych wyrazów
początkowych wyrazów 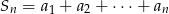 wyraża się wzorem:
wyraża się wzorem: 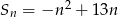 .
.
- Wyznacz wzór na
 –ty wyraz ciągu
–ty wyraz ciągu 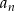 .
. - Oblicz
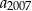 .
. - Wyznacz liczbę
 , dla której
, dla której 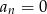 . .
. .
Krawędzie prostopadłościanu wychodzące z jednego wierzchołka tworzą ciąg arytmetyczny o pierwszym wyrazie 5 i różnicy 2. Wyznacz pole powierzchni całkowitej tego prostopadłościanu.
Liczby 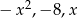 w podanej kolejności tworzą ciąg geometryczny. Oblicz
w podanej kolejności tworzą ciąg geometryczny. Oblicz  .
.
Iloczyn dziewięciu kolejnych początkowych wyrazów pewnego ciągu geometrycznego wynosi 512. Oblicz piąty wyraz tego ciągu.
Iloczyn siedmiu kolejnych początkowych wyrazów pewnego ciągu geometrycznego wynosi 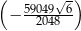 . Oblicz czwarty wyraz tego ciągu.
. Oblicz czwarty wyraz tego ciągu.
Liczby 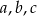 mają tę własność, że każdy z ciągów:
mają tę własność, że każdy z ciągów: 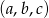 ,
, 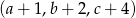 i
i 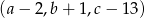 jest ciągiem geometrycznym. Oblicz
jest ciągiem geometrycznym. Oblicz 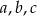 .
.
Suma szóstego i szesnastego wyrazu ciągu arytmetycznego 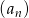 jest równa 5, a iloczyn wyrazu ósmego i dwunastego równy jest 3. Wyznacz wzór na wyraz ogólny ciągu
jest równa 5, a iloczyn wyrazu ósmego i dwunastego równy jest 3. Wyznacz wzór na wyraz ogólny ciągu 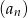 .
.
Oblicz granicę 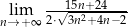 .
.
Dane są dwa różne ciągi: arytmetyczny i geometryczny. Każdy z nich składa się z trzech wyrazów dodatnich. Pierwsze i ostatnie wyrazy tych ciagów są równe. Suma wyrazów którego ciągu jest większa?
W kwadrat o boku  wpisujemy okrąg. W ten okrąg wpisujemy kwadrat, w który wpisujemy okrąg itd. W ten sposób powstanie nieskończony ciąg kwadratów. Oblicz sumę pól wszystkich tych kwadratów.
wpisujemy okrąg. W ten okrąg wpisujemy kwadrat, w który wpisujemy okrąg itd. W ten sposób powstanie nieskończony ciąg kwadratów. Oblicz sumę pól wszystkich tych kwadratów.
W kwadrat o boku  wpisujemy okrąg. W ten okrąg wpisujemy kwadrat, w który wpisujemy okrąg itd. W ten sposób powstanie nieskończony ciąg kwadratów. Oblicz sumę obwodów wszystkich tych kwadratów.
wpisujemy okrąg. W ten okrąg wpisujemy kwadrat, w który wpisujemy okrąg itd. W ten sposób powstanie nieskończony ciąg kwadratów. Oblicz sumę obwodów wszystkich tych kwadratów.
W kwadrat 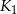 o boku
o boku  wpisujemy kwadrat
wpisujemy kwadrat 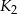 , którego wierzchołki są środkami boków kwadratu
, którego wierzchołki są środkami boków kwadratu 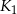 , następnie w kwadrat
, następnie w kwadrat 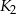 wpisujemy kwadrat
wpisujemy kwadrat 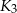 , którego wierzchołki są środkami boków
, którego wierzchołki są środkami boków 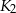 i tak dalej. Oblicz sumę pól otrzymanego w ten sposób nieskończonego ciągu kwadratów.
i tak dalej. Oblicz sumę pól otrzymanego w ten sposób nieskończonego ciągu kwadratów.
Wykaż, że dla dowolnego ciągu arytmetycznego zachodzi równość 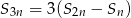 , gdzie
, gdzie 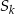 oznacza sumę
oznacza sumę 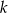 początkowych wyrazów ciągu.
początkowych wyrazów ciągu.
Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny, w którym środkowy wyraz jest równy 8. Wyznacz długości boków trójkąta, oblicz jego pole oraz promień okręgu opisanego na tym trójkącie.
Liczby 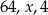 są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz piąty wyraz tego ciągu.
są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz piąty wyraz tego ciągu.
Oblicz sumę wszystkich liczb mniejszych od 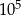 , które mogą być zapisane w postaci
, które mogą być zapisane w postaci 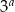 dla pewnej nieujemnej liczby całkowitej
dla pewnej nieujemnej liczby całkowitej  .
.
Oblicz granicę 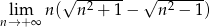 .
.
Oblicz granicę 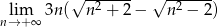 .
.
Oblicz granicę 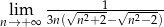 .
.
Oblicz granicę 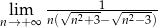 .
.
Oblicz granicę 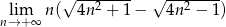 .
.
Oblicz granicę 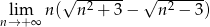 .
.
Oblicz granicę 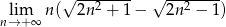 .
.
Oblicz granicę 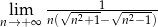 .
.
Oblicz granicę 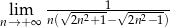 .
.
Oblicz granicę 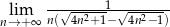 .
.
Nieskończony ciąg liczbowy 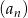 określony jest wzorem:
określony jest wzorem:
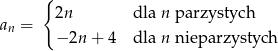
- Wyznacz sumę dwudziestu początkowych wyrazów ciągu.
- Zbadaj, czy istnieje wyraz ciągu równy 5. Odpowiedź uzasadnij.
W ciągu arytmetycznym 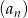 dany jest wyraz
dany jest wyraz 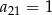 oraz suma 21 początkowych wyrazów
oraz suma 21 początkowych wyrazów 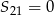 . Oblicz pierwszy wyraz oraz różnicę tego ciągu.
. Oblicz pierwszy wyraz oraz różnicę tego ciągu.
Suma czterdziestu początkowych wyrazów ciągu arytmetycznego 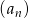 , określonego dla
, określonego dla 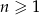 , jest równa 40. Ponadto
, jest równa 40. Ponadto 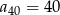 . Oblicz różnicę tego ciągu.
. Oblicz różnicę tego ciągu.
Suma trzydziestu początkowych wyrazów ciągu arytmetycznego 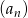 , określonego dla
, określonego dla 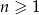 , jest równa 30. Ponadto
, jest równa 30. Ponadto 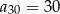 . Oblicz różnicę tego ciągu.
. Oblicz różnicę tego ciągu.
Oblicz 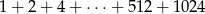 .
.

