Zbadaj, czy ciąg 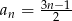 jest arytmetyczny.
jest arytmetyczny.
/Szkoła średnia/Ciągi
Zbadaj, czy ciąg 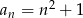 jest arytmetyczny.
jest arytmetyczny.
Zbadaj, czy ciąg 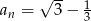 jest arytmetyczny.
jest arytmetyczny.
Udowodnij, że w ciągu geometrycznym 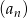 o wyrazach dodatnich iloczyn
o wyrazach dodatnich iloczyn 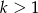 początkowych wyrazów ciągu jest równy
początkowych wyrazów ciągu jest równy 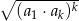 .
.
Iloczyn pierwszego i piątego wyrazu malejącego ciągu arytmetycznego 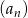 jest równy 160, a przy dzieleniu wyrazu drugiego przez wyraz piąty otrzymujemy 2 i resztę jeden. Wyznacz różnicę tego ciągu.
jest równy 160, a przy dzieleniu wyrazu drugiego przez wyraz piąty otrzymujemy 2 i resztę jeden. Wyznacz różnicę tego ciągu.
Iloczyn pierwszego i czwartego wyrazu malejącego ciągu arytmetycznego 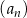 jest równy 253, a przy dzieleniu wyrazu drugiego przez wyraz piąty otrzymujemy 2 i resztę pięć. Wyznacz różnicę tego ciągu.
jest równy 253, a przy dzieleniu wyrazu drugiego przez wyraz piąty otrzymujemy 2 i resztę pięć. Wyznacz różnicę tego ciągu.
Dany jest ciąg 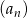 o wyrazie ogólnym
o wyrazie ogólnym 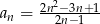 .
.
- Uzasadnij, że wszystkie wyrazy ciągu
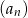 są liczbami całkowitymi.
są liczbami całkowitymi. - Który wyraz jest równy 5?
- Różnica sześcianów dwóch kolejnych wyrazów ciągu
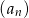 wynosi
wynosi 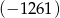 . Wyznacz te wyrazy.
. Wyznacz te wyrazy.
Udowodnij, że jeżeli ciąg 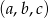 jest jednocześnie arytmetyczny i geometryczny to
jest jednocześnie arytmetyczny i geometryczny to 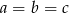 .
.
Wyznacz iloraz niezerowego ciągu geometrycznego, w którym suma 10 początkowych wyrazów jest 5 razy większa od sumy pierwszych 5 wyrazów.
Dany jest nieskończony ciąg okręgów 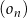 o równaniach
o równaniach 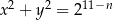 ,
, 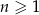 . Niech
. Niech 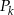 będzie pierścieniem ograniczonym zewnętrznym okręgiem
będzie pierścieniem ograniczonym zewnętrznym okręgiem 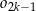 i wewnętrznym okręgiem
i wewnętrznym okręgiem 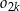 . Oblicz sumę pól wszystkich pierścieni
. Oblicz sumę pól wszystkich pierścieni 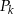 , gdzie
, gdzie 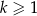 .
.
Dany jest nieskończony ciąg okręgów 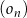 o równaniach
o równaniach 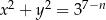 ,
, 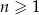 . Niech
. Niech 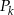 będzie pierścieniem ograniczonym zewnętrznym okręgiem
będzie pierścieniem ograniczonym zewnętrznym okręgiem 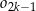 i wewnętrznym okręgiem
i wewnętrznym okręgiem 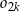 . Oblicz sumę pól wszystkich pierścieni
. Oblicz sumę pól wszystkich pierścieni 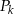 , gdzie
, gdzie 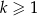 .
.
Wykaż, że jeżeli 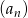 jest ciągiem geometrycznym, to ciąg
jest ciągiem geometrycznym, to ciąg 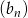 o wyrazie ogólnym określonym wzorem
o wyrazie ogólnym określonym wzorem 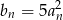 też jest ciągiem geometrycznym.
też jest ciągiem geometrycznym.
Ciąg 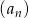 jest ciągiem geometrycznym. Wykaz, że ciąg
jest ciągiem geometrycznym. Wykaz, że ciąg 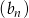 określony wzorem
określony wzorem 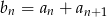 jest również ciągiem geometrycznym.
jest również ciągiem geometrycznym.
Określamy kwadraty 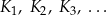 następująco:
następująco:
-
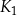 jest kwadratem o boku długości
jest kwadratem o boku długości 
-
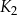 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 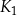 i dzieli ten bok w stosunku 1 : 3
i dzieli ten bok w stosunku 1 : 3 -
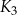 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 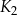 i dzieli ten bok w stosunku 1 : 3
i dzieli ten bok w stosunku 1 : 3
i ogólnie, dla każdej liczby naturalnej 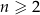 ,
,
-
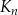 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 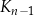 i dzieli ten bok w stosunku 1 : 3.
i dzieli ten bok w stosunku 1 : 3.
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
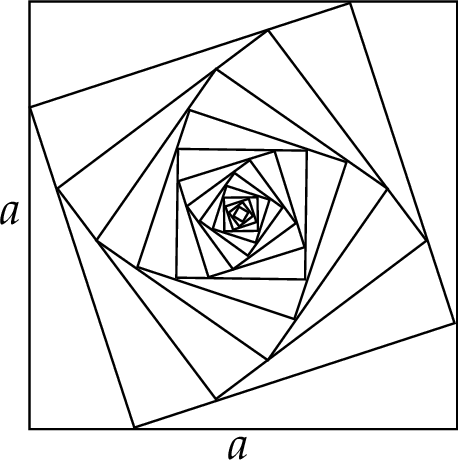
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu.
Określamy kwadraty 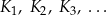 następująco:
następująco:
-
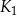 jest kwadratem o boku długości
jest kwadratem o boku długości 
-
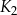 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 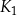 i dzieli ten bok w stosunku 1 : 2
i dzieli ten bok w stosunku 1 : 2 -
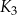 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 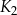 i dzieli ten bok w stosunku 1 : 2
i dzieli ten bok w stosunku 1 : 2
i ogólnie, dla każdej liczby naturalnej 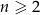 ,
,
-
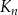 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 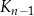 i dzieli ten bok w stosunku 1 : 2.
i dzieli ten bok w stosunku 1 : 2.
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
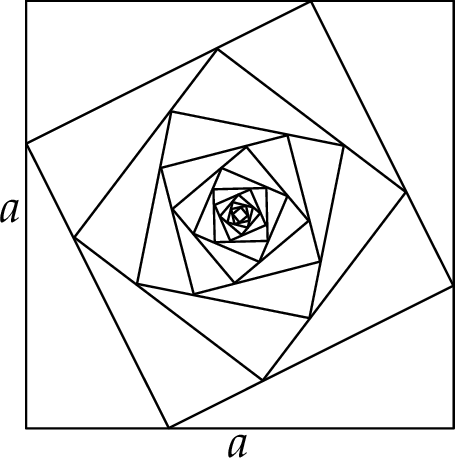
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu.
Wiadomo, że liczby 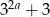 ,
, 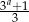 ,
, 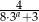 są odpowiednio pierwszym, drugim i trzecim wyrazem nieskończonego ciągu geometrycznego. Wyznacz
są odpowiednio pierwszym, drugim i trzecim wyrazem nieskończonego ciągu geometrycznego. Wyznacz  . Dla wyznaczonej wartości
. Dla wyznaczonej wartości  zapisz wzór tego ciągu i oblicz sumę jego wszystkich wyrazów.
zapisz wzór tego ciągu i oblicz sumę jego wszystkich wyrazów.
Funkcje 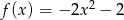 ,
, 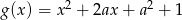 i
i 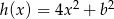 mają tę własność, że dla każdej liczby rzeczywistej
mają tę własność, że dla każdej liczby rzeczywistej  , liczby
, liczby 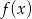 ,
,  i
i 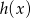 tworzą (w pewnej kolejności) ciąg geometryczny. Wyznacz możliwe ilorazy tego ciągu.
tworzą (w pewnej kolejności) ciąg geometryczny. Wyznacz możliwe ilorazy tego ciągu.
Funkcje 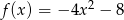 ,
, 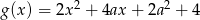 i
i 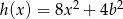 mają tę własność, że dla każdej liczby rzeczywistej
mają tę własność, że dla każdej liczby rzeczywistej  , wartości funkcji
, wartości funkcji 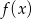 ,
, 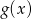 i
i 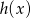 tworzą w pewnej kolejności trzywyrazowy ciąg geometryczny. Oblicz iloraz tego ciągu.
tworzą w pewnej kolejności trzywyrazowy ciąg geometryczny. Oblicz iloraz tego ciągu.
W dziewięciowyrazowym ciągu arytmetycznym, o pierwszym wyrazie równym 4, wyraz pierwszy, trzeci i siódmy tworzą ciąg geometryczny. Oblicz sumę wyrazów tego ciągu arytmetycznego
Obroty pewnej firmy w pierwszych trzech kwartałach 2007 roku utworzyły ciąg geometryczny, a w ciągu ostatnich trzech kwartałów ciąg arytmetyczny. W drugim kwartale obroty firmy wynosiły 15 000 zł, a w czwartym 22 500 zł. Oblicz średnie miesięczne obroty firmy.
Liczby 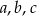 są trzema kolejnymi wyrazami ciągu arytmetycznego, a liczby
są trzema kolejnymi wyrazami ciągu arytmetycznego, a liczby 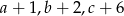 – trzema kolejnymi wyrazami ciągu geometrycznego. Znajdź liczby
– trzema kolejnymi wyrazami ciągu geometrycznego. Znajdź liczby 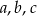 wiedząc, że ich suma jest równa 12.
wiedząc, że ich suma jest równa 12.
Liczby 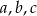 są – odpowiednio – pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Suma tych liczb jest równa 27. Ciąg
są – odpowiednio – pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Suma tych liczb jest równa 27. Ciąg 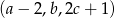 jest geometryczny. Wyznacz liczby
jest geometryczny. Wyznacz liczby 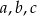 .
.
Suma wyrazów trzywyrazowego ciągu arytmetycznego 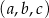 jest równa 36. Ciąg
jest równa 36. Ciąg
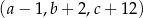
jest geometryczny. Oblicz 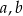 i
i  .
.
Trzy liczby tworzą ciąg arytmetyczny. Ich suma jest równa 45. Jeśli pierwszą i trzecią liczbę pozostawimy bez zmian, a drugą pomniejszymy o 3 to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz wyrazy ciągu arytmetycznego.
Liczby 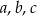 , spełniające warunek
, spełniające warunek 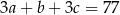 , są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Ciąg
, są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Ciąg 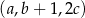 jest geometryczny. Wyznacz liczby
jest geometryczny. Wyznacz liczby 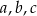 oraz podaj wyrazy ciągu geometrycznego.
oraz podaj wyrazy ciągu geometrycznego.
Ciąg 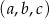 jest arytmetyczny i
jest arytmetyczny i 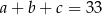 . Ciąg
. Ciąg 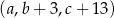 jest geometryczny. Oblicz
jest geometryczny. Oblicz 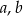 i
i  .
.
Trzy liczby tworzą ciąg arytmetyczny. Ich suma jest równa 60. Jeśli pierwszą i trzecią liczbę pozostawimy bez zmian, a drugą pomniejszymy o cztery, to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz wyrazy ciągu arytmetycznego.
Trzy liczby, których suma jest równa 45, tworzą ciąg arytmetyczny. Jeśli drugą liczbę powiększymy o 3, a trzecią liczbę powiększymy o 9, to otrzymamy ciąg geometryczny. Wyznacz te liczby.
Ciąg liczbowy 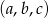 jest arytmetyczny i
jest arytmetyczny i 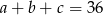 , natomiast ciąg
, natomiast ciąg 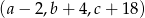 jest geometryczny. Oblicz
jest geometryczny. Oblicz 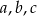 .
.
Trzy liczby dodatnie tworzą ciąg arytmetyczny. Średnia arytmetyczna tych liczb jest równa 10. Jeśli od pierwszej odejmiemy 2, drugą pozostawimy bez zmian, a do trzeciej dodamy 7, to otrzymamy ciąg geometryczny. Wyznacz te liczby.
Ciąg 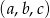 jest ciągiem arytmetycznym. Suma jego wyrazów jest równa 18. Jeżeli pierwszą z liczb zmniejszymy o 25%, a trzecią zwiększymy o 50%, to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz liczby
jest ciągiem arytmetycznym. Suma jego wyrazów jest równa 18. Jeżeli pierwszą z liczb zmniejszymy o 25%, a trzecią zwiększymy o 50%, to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz liczby 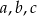 .
.
Trzy liczby 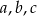 których suma jest równa 15, tworzą w tej kolejności ciąg arytmetyczny. Jeśli do pierwszej z tych liczb dodać 2, od drugiej odjąć 1, a trzecią podzielić przez 2, to tak otrzymane liczby (w tej kolejności) utworzą ciąg geometryczny malejący. Wyznacz iloraz tego ciągu geometrycznego.
których suma jest równa 15, tworzą w tej kolejności ciąg arytmetyczny. Jeśli do pierwszej z tych liczb dodać 2, od drugiej odjąć 1, a trzecią podzielić przez 2, to tak otrzymane liczby (w tej kolejności) utworzą ciąg geometryczny malejący. Wyznacz iloraz tego ciągu geometrycznego.
Trzy liczby dodatnie tworzą ciąg arytmetyczny. Średnia arytmetyczna tych liczb jest równa 8. Jeśli od pierwszej odejmiemy 1, drugą pozostawimy bez zmian, a do trzeciej dodamy 5, to otrzymamy ciąg geometryczny. Wyznacz te liczby.
Trzy liczby ciąg arytmetyczny. Ich suma jest równa 15. Jeśli pierwszą i trzecią liczbę pozostawimy bez zmian, a drugą pomniejszymy o jeden to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz wyrazy ciągu arytmetycznego.
Ciąg liczbowy 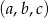 jest arytmetyczny i
jest arytmetyczny i 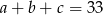 , natomiast ciąg
, natomiast ciąg 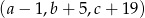 jest geometryczny. Oblicz
jest geometryczny. Oblicz 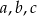 .
.
Trzy liczby tworzą ciąg arytmetyczny. Ich suma jest równa 15. Jeśli pierwszą i trzecią liczbę pozostawimy bez zmian, a drugą pomniejszymy o jeden to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz wyrazy ciągu arytmetycznego.
Trzy liczby tworzą ciąg arytmetyczny. Ich suma jest równa 30. Jeśli pierwszą i trzecią liczbę pozostawimy bez zmian, a drugą pomniejszymy o dwa to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz wyrazy ciągu arytmetycznego.
O liczbach 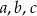 wiemy, że ciąg
wiemy, że ciąg 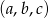 jest arytmetyczny i
jest arytmetyczny i 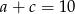 , zaś ciąg
, zaś ciąg 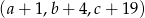 jest geometryczny. Wyznacz te liczby.
jest geometryczny. Wyznacz te liczby.
Dany jest ciąg 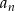 o wyrazie ogólnym
o wyrazie ogólnym 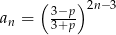 .
.
- Udowodnij, że ciąg
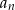 jest ciągiem geometrycznym.
jest ciągiem geometrycznym. - Wyznacz te wartości parametru
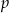 , dla których istnieje suma wszystkich wyrazów ciągu
, dla których istnieje suma wszystkich wyrazów ciągu 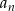 . Oblicz tę sumę.
. Oblicz tę sumę. - Wyznacz te wartości parametru
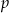 , dla których ciąg
, dla których ciąg 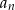 jest malejący.
jest malejący.
Wyznacz drugi, trzeci i czwarty wyraz ciągu określonego wzorem rekurencyjnym:
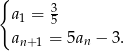
Dla wyznaczonych wyrazów znajdź taką liczbę  , aby ciąg
, aby ciąg 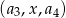 był ciągiem geometrycznym.
był ciągiem geometrycznym.
Oblicz sześć początkowych wyrazów ciągu arytmetycznego jeśli 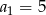 oraz
oraz 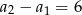 .
.
Oblicz sześć początkowych wyrazów ciągu arytmetycznego 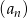 , jeśli
, jeśli 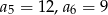 .
.
Oblicz sześć początkowych wyrazów ciągu arytmetycznego 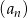 , jeśli
, jeśli 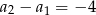 oraz
oraz 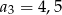 .
.
Ciąg 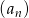 określony jest wzorem
określony jest wzorem 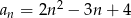 .
.
- Trzeci i piąty wyraz ciągu
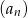 są odpowiednio równe szóstemu i dziewiętnastemu wyrazowi ciągu arytmetycznego
są odpowiednio równe szóstemu i dziewiętnastemu wyrazowi ciągu arytmetycznego 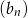 . Ile początkowych wyrazów ciągu arytmetycznego
. Ile początkowych wyrazów ciągu arytmetycznego 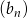 należy dodać, aby otrzymana suma była nie mniejsza od 483?
należy dodać, aby otrzymana suma była nie mniejsza od 483? - Piąty oraz trzeci wyraz ciągu
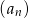 są odpowiednio równe pierwszemu i drugiemu wyrazowi nieskończonego ciągu geometrycznego
są odpowiednio równe pierwszemu i drugiemu wyrazowi nieskończonego ciągu geometrycznego 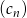 . Który wyraz ciągu
. Który wyraz ciągu 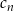 jest równy
jest równy 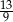 ?
?
Ciąg 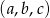 jest geometryczny i
jest geometryczny i 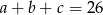 , zaś ciąg
, zaś ciąg 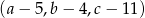 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz 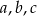 .
.
Trzy liczby, których suma jest równa 105, tworzą ciąg geometryczny. Jeśli pierwszą liczbę zmniejszymy o 45, to otrzymamy ciąg arytmetyczny. Wyznacz te liczby.
Trzy liczby, których suma jest równa 52, tworzą ciąg geometryczny. Jeśli pierwszą liczbę zmniejszymy o 16, to otrzymamy ciąg arytmetyczny. Wyznacz te liczby.
Ciąg 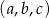 jest geometryczny, ciąg
jest geometryczny, ciąg 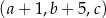 jest malejącym ciągiem arytmetycznym oraz
jest malejącym ciągiem arytmetycznym oraz 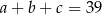 . Oblicz
. Oblicz 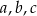 .
.
Ciąg 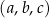 jest trzywyrazowym ciągiem geometrycznym o wyrazach dodatnich. Ciąg
jest trzywyrazowym ciągiem geometrycznym o wyrazach dodatnich. Ciąg
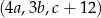
jest trzywyrazowym ciągiem arytmetycznym. Ponadto, spełniony jest warunek 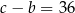 . Oblicz
. Oblicz 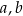 oraz
oraz  .
.
Ciąg 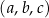 jest trzywyrazowym ciągiem geometrycznym o wyrazach dodatnich. Ciąg
jest trzywyrazowym ciągiem geometrycznym o wyrazach dodatnich. Ciąg
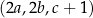
jest trzywyrazowym ciągiem arytmetycznym. Ponadto, spełniony jest warunek 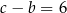 . Oblicz
. Oblicz 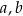 oraz
oraz  .
.
Suma trzech liczb będących kolejnymi wyrazami rosnącego ciągu geometrycznego jest równa 52. Jeżeli do pierwszej liczby dodamy 2, do drugiej 12, a do trzeciej 6, to otrzymamy trzy kolejne wyrazy ciągu arytmetycznego. Wyznacz ten ciąg.
Liczby 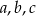 są kolejnymi wyrazami ciągu arytmetycznego, zaś liczby
są kolejnymi wyrazami ciągu arytmetycznego, zaś liczby 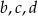 są kolejnymi wyrazami ciągu geometrycznego. Suma pierwszej trójki liczb wynosi 12, a drugiej 19. Wyznacz liczby
są kolejnymi wyrazami ciągu geometrycznego. Suma pierwszej trójki liczb wynosi 12, a drugiej 19. Wyznacz liczby 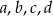 .
.

