Oblicz granicę 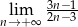 .
.
/Szkoła średnia/Ciągi
Oblicz granicę 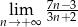 .
.
Oblicz granicę 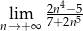 .
.
Oblicz granicę 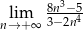 .
.
Oblicz granicę 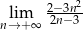 .
.
Oblicz granicę 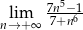 .
.
Oblicz granicę 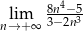 .
.
Oblicz granicę 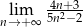 .
.
Oblicz granicę 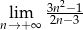 .
.
Oblicz granicę 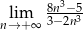 .
.
Oblicz granicę 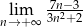 .
.
Oblicz granicę 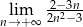 .
.
Oblicz granicę 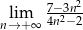 .
.
Oblicz granicę 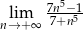 .
.
Oblicz granicę 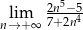 .
.
Oblicz granicę 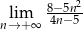 .
.
Oblicz granicę 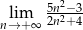 .
.
Oblicz granicę 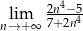 .
.
Oblicz granicę 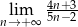 .
.
Oblicz granicę 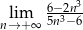 .
.
Oblicz granicę 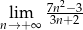 .
.
Oblicz granicę 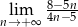 .
.
Oblicz granicę 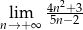 .
.
Oblicz granicę 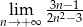 .
.
Oblicz granicę 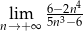 .
.
Oblicz granicę 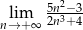 .
.
Oblicz granicę 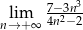 .
.
Oblicz granicę 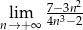 .
.
Oblicz granicę 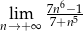 .
.
Oblicz granicę 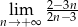 .
.
Oblicz granicę 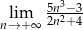 .
.
Oblicz granicę 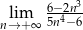 .
.
Oblicz granicę 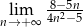 .
.
Liczby 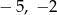 oraz 1 w podanej kolejności są trzema początkowymi wyrazami ciągu arytmetycznego
oraz 1 w podanej kolejności są trzema początkowymi wyrazami ciągu arytmetycznego  . Oblicz ile wyrazów ciągu
. Oblicz ile wyrazów ciągu  należy do przedziału
należy do przedziału 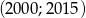 .
.
Liczby 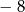 i 3 w podanej kolejności są dwoma początkowymi wyrazami ciągu arytmetycznego
i 3 w podanej kolejności są dwoma początkowymi wyrazami ciągu arytmetycznego 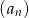 . Oblicz ile wyrazów ciągu
. Oblicz ile wyrazów ciągu 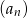 należy do przedziału
należy do przedziału 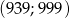 .
.
Dziesiąty wyraz ciągu arytmetycznego 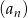 jest o 48 mniejszy od sumy jego pierwszych 7 wyrazów. Oblicz sumę pierwszych 33 wyrazów tego ciągu wiedząc, że iloczyn
jest o 48 mniejszy od sumy jego pierwszych 7 wyrazów. Oblicz sumę pierwszych 33 wyrazów tego ciągu wiedząc, że iloczyn 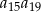 ma najmniejszą możliwą wartość.
ma najmniejszą możliwą wartość.
Niech 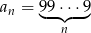 . Oblicz sumę 12 początkowych wyrazów ciągu
. Oblicz sumę 12 początkowych wyrazów ciągu 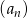 .
.
Niech 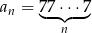 . Oblicz sumę 12 początkowych wyrazów ciągu
. Oblicz sumę 12 początkowych wyrazów ciągu 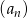 .
.
Dany jest ciąg 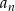 o wyrazie ogólnym
o wyrazie ogólnym 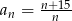 .
.
- Oblicz, ile wyrazów ciągu
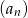 jest większych od 3.
jest większych od 3. - Wyznacz wszystkie te wyrazy ciągu
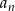 , które są liczbami naturalnymi.
, które są liczbami naturalnymi.
Pierwszy wyraz ciągu geometrycznego 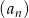 jest równy 6, a iloraz dziesiątego wyrazu i wyrazu szóstego równy jest 16. Wiedząc że ciąg
jest równy 6, a iloraz dziesiątego wyrazu i wyrazu szóstego równy jest 16. Wiedząc że ciąg 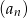 nie jest monotoniczny znajdź
nie jest monotoniczny znajdź
- jego iloraz,
- jego piąty wyraz,
- wzór na wyraz ogólny ciągu.
Wyznacz te wartości  , dla których istnieje suma nieskończonego ciągu geometrycznego
, dla których istnieje suma nieskończonego ciągu geometrycznego
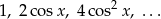
Ciąg 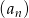 , gdzie
, gdzie 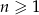 dany jest wzorem rekurencyjnym
dany jest wzorem rekurencyjnym
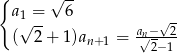
- Oblicz sumę 21 początkowych wyrazów tego ciągu.
- Wyznacz wszystkie liczby naturalne
 , dla których spełniona jest nierówność
, dla których spełniona jest nierówność 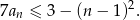
Ciąg 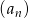 jest określony dla
jest określony dla 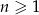 i spełnia warunek
i spełnia warunek
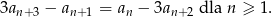
Oblicz sumę dwóch początkowych wyrazów ciągu 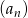 jeżeli suma wszystkich jego wyrazów jest równa 2016.
jeżeli suma wszystkich jego wyrazów jest równa 2016.
Obliczyć granicę 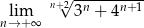 .
.
Dla jakich 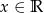 liczby
liczby 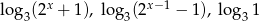 tworzą, w podanej kolejności, ciąg arytmetyczny. Wyznacz różnicę tego ciągu.
tworzą, w podanej kolejności, ciąg arytmetyczny. Wyznacz różnicę tego ciągu.
Dany jest ciąg 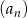 określony wzorem
określony wzorem 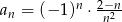 dla
dla 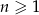 . Oblicz
. Oblicz 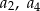 i
i 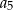 .
.
Dany jest ciąg 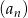 określony wzorem
określony wzorem 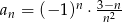 dla
dla 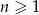 . Oblicz
. Oblicz 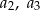 i
i 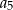 .
.
Dany jest ciąg 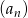 określony rekurencyjnie
określony rekurencyjnie
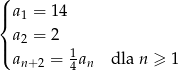
Oblicz sumę 18 początkowych wyrazów ciągu 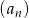 .
.
Dany jest ciąg 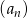 o wyrazie ogólnym
o wyrazie ogólnym 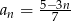 , dla
, dla 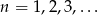 .
.
- Sprawdź, czy ciąg
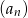 jest arytmetyczny.
jest arytmetyczny. - Oblicz, dla jakiej wartości
 liczby
liczby 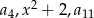 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Długości boków trójkąta prostokątnego o polu 96 tworzą ciąg arytmetyczny. Oblicz:
- długości boków tego trójkąta,
- pole koła wpisanego w ten trójkąt.
Drugi wyraz ciągu arytmetycznego jest równy 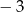 , dziesiąty wyraz jest równy 21. Wyznacz pierwszy wyraz i różnicę tego ciągu.
, dziesiąty wyraz jest równy 21. Wyznacz pierwszy wyraz i różnicę tego ciągu.
W ciągu arytmetycznym 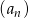 trzeci wyraz jest równy 11, a siódmy 21. Wyznacz pierwszy wyraz i różnicę tego ciągu.
trzeci wyraz jest równy 11, a siódmy 21. Wyznacz pierwszy wyraz i różnicę tego ciągu.
Wiedząc, że ciąg 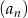 jest arytmetyczny i mając dane:
jest arytmetyczny i mając dane: 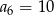 i
i 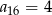 , oblicz
, oblicz 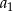 oraz różnicę
oraz różnicę  tego ciągu.
tego ciągu.
Trzeci wyraz ciągu arytmetycznego jest równy 10, a siódmy 42. Wyznacz pierwszy wyraz i różnicę tego ciągu.
Dany jest ciąg arytmetyczny 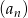 określony dla
określony dla 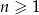 , w którym
, w którym 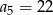 oraz
oraz 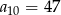 . Oblicz pierwszy wyraz
. Oblicz pierwszy wyraz 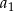 i różnicę
i różnicę  tego ciągu.
tego ciągu.
Liczby 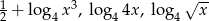 w podanej kolejności, dla pewnej rzeczywistej wartości
w podanej kolejności, dla pewnej rzeczywistej wartości  , są trzema kolejnymi początkowymi wyrazami nieskończonego ciągu arytmetycznego. Wyznacz
, są trzema kolejnymi początkowymi wyrazami nieskończonego ciągu arytmetycznego. Wyznacz  oraz sumę czterdziestu początkowych wyrazów tego ciągu.
oraz sumę czterdziestu początkowych wyrazów tego ciągu.
Dany jest ciąg geometryczny, w którym 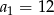 i
i 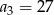 .
.
- Ile jest ciągów spełniających podane warunki? Odpowiedź uzasadnij.
- Oblicz wyraz
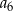 tego ciągu, który jest rosnący. Wynik podaj w postaci ułamka dziesiętnego.
tego ciągu, który jest rosnący. Wynik podaj w postaci ułamka dziesiętnego.
Kolejne cyfry dodatniej liczby trzycyfrowej tworzą ciąg geometryczny. Suma cyfr jedności i dziesiątek jest o jeden większa od cyfry setek. Jeżeli od szukanej liczby odejmiemy liczbę złożoną z tych samych cyfr, lecz napisanych w odwrotnej kolejności to otrzymamy 495. Znajdź tę liczbę.
Znajdź ogólny wyraz ciągu arytmetycznego 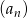 wiedząc, że
wiedząc, że 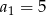 oraz
oraz 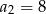 .
.

