Wykaż, że trójkąt, którego długości boków są trzema kolejnymi wyrazami ciągu geometrycznego, miary kątów zaś trzema kolejnymi wyrazami ciągu arytmetycznego jest trójkątem równobocznym.
/Szkoła średnia/Ciągi
Liczby
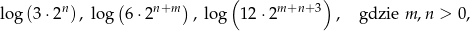
są odpowiednio pierwszym, piątym i dziewiątym wyrazem ciągu arytmetycznego. Wyznacz różnicę tego ciągu.
Wyznacz wzór ogólny ciągu geometrycznego wiedząc, że 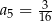 oraz
oraz 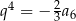 .
.
Oblicz granicę 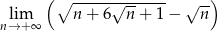 .
.
Oblicz granicę 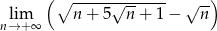 .
.
Oblicz granicę 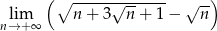 .
.
Oblicz granicę 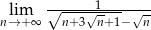 .
.
Oblicz granicę 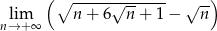 .
.
Oblicz granicę 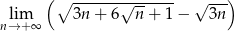 .
.
Oblicz granicę 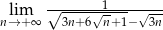 .
.
Oblicz granicę 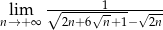 .
.
Oblicz granicę 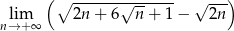 .
.
Oblicz granicę 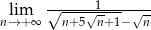 .
.
Oblicz sumę nieskończonego szeregu geometrycznego
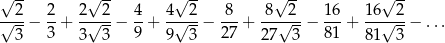
Oblicz sumę nieskończonego szeregu geometrycznego
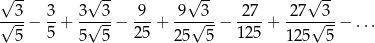
Suma ośmiu początkowych wyrazów ciągu geometrycznego 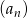 , określonego dla
, określonego dla 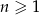 , jest równa 55760. Ponadto
, jest równa 55760. Ponadto 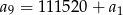 . Oblicz iloraz tego ciągu.
. Oblicz iloraz tego ciągu.
Ania układa szklane kulki w figury pokazane na rysunku, na którym pokazane są pierwsze trzy figury.
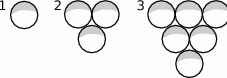
- Niech
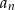 będzie różnicą liczby kulek w
będzie różnicą liczby kulek w 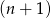 –ej i
–ej i  –tej figurze. Wypisz pierwszych 5 wyrazów ciągu
–tej figurze. Wypisz pierwszych 5 wyrazów ciągu 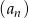 .
. - Uzasadnij, że
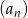 jest ciągiem arytmetycznym i oblicz ile potrzeba kulek do ułożenia 20 figury.
jest ciągiem arytmetycznym i oblicz ile potrzeba kulek do ułożenia 20 figury.
Dany jest okrąg 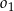 o promieniu
o promieniu  . Wewnątrz tego okręgu narysowano okrąg
. Wewnątrz tego okręgu narysowano okrąg 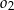 styczny wewnętrznie o średnicy
styczny wewnętrznie o średnicy  , wewnątrz okręgu
, wewnątrz okręgu 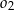 znów narysowano okrąg styczny wewnętrznie o średnicy
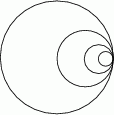
znów narysowano okrąg styczny wewnętrznie o średnicy 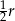 itd. Czynność tę powtórzono nieskończenie wiele razy. Wykaż, że suma długości okręgów
itd. Czynność tę powtórzono nieskończenie wiele razy. Wykaż, że suma długości okręgów 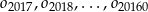 jest mniejsza od długości okręgu
jest mniejsza od długości okręgu 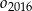 .
.
Nieskończony ciąg geometryczny 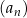 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 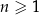 . Suma wszystkich wyrazów ciągu
. Suma wszystkich wyrazów ciągu 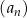 o numerach nieparzystych jest równa 16, tj.
o numerach nieparzystych jest równa 16, tj.
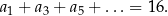
Ponadto 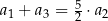 . Wyznacz wzór ogólny na n–ty wyraz ciągu
. Wyznacz wzór ogólny na n–ty wyraz ciągu 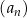 .
.
Ciąg 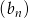 jest arytmetyczny i
jest arytmetyczny i 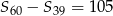 , gdzie
, gdzie 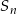 oznacza sumę
oznacza sumę  początkowych wyrazów tego ciągu. Oblicz
początkowych wyrazów tego ciągu. Oblicz  , wiedząc, że liczby
, wiedząc, że liczby 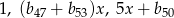 tworzą rosnący ciąg geometryczny.
tworzą rosnący ciąg geometryczny.
Dany jest ciąg 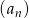 określony wzorem
określony wzorem 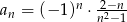 dla
dla 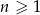 . Oblicz
. Oblicz 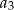 i
i 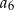 .
.
Ciągi 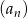 i
i 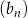 , gdzie
, gdzie 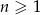 są ciągami arytmetycznymi. Wykaż, że jeżeli ciąg
są ciągami arytmetycznymi. Wykaż, że jeżeli ciąg 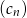 zdefiniowany wzorem
zdefiniowany wzorem 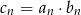 (
(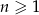 ) jest ciągiem arytmetycznym, to różnica jednego z ciągów
) jest ciągiem arytmetycznym, to różnica jednego z ciągów 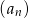 lub
lub 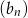 jest równa zeru.
jest równa zeru.
Dla pewnych liczb 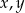 wartości wyrażeń
wartości wyrażeń 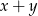 ,
, 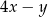 ,
, 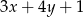 ,
, 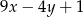 są początkowymi, kolejnymi wyrazami ciągu arytmetycznego. Oblicz, ile początkowych wyrazów tego ciągu należy wziąć, aby ich suma była większa od 20100.
są początkowymi, kolejnymi wyrazami ciągu arytmetycznego. Oblicz, ile początkowych wyrazów tego ciągu należy wziąć, aby ich suma była większa od 20100.
Iloraz ciągu geometrycznego 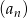 jest równy
jest równy 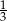 , a suma jego pięciu początkowych wyrazów wynosi
, a suma jego pięciu początkowych wyrazów wynosi 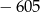 . Znajdź pierwszy wyraz ciągu
. Znajdź pierwszy wyraz ciągu 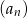 oraz określ jego monotoniczność.
oraz określ jego monotoniczność.
Dany jest ciąg arytmetyczny o pierwszym wyrazie 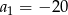 i różnicy
i różnicy 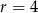 . Wyznacz liczbę
. Wyznacz liczbę  , dla której suma częściowa
, dla której suma częściowa 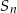 jest równa 780.
jest równa 780.
Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg geometryczny o sumie 19. Objętość prostopadłościanu jest równa 216. Wyznacz pole powierzchni całkowitej tego prostopadłościanu.
Dla jakich  liczby
liczby 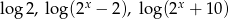 są kolejnymi wyrazami ciągu arytmetycznego? Oblicz różnicę tego ciągu.
są kolejnymi wyrazami ciągu arytmetycznego? Oblicz różnicę tego ciągu.
Rozważmy ciąg trójkątów równobocznych takich, że długość boku pierwszego trójkąta jest równa  , zaś bok każdego następnego jest równy połowie wysokości poprzedniego. Oblicz sumę wszystkich pól tak utworzonych trójkątów.
, zaś bok każdego następnego jest równy połowie wysokości poprzedniego. Oblicz sumę wszystkich pól tak utworzonych trójkątów.
W ciągu arytmetycznym 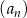 , określonym dla
, określonym dla 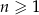 , wyraz szósty jest równy 3, a wyraz dziesiąty jest równy 15. Oblicz dla jakich wartości
, wyraz szósty jest równy 3, a wyraz dziesiąty jest równy 15. Oblicz dla jakich wartości  suma
suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 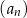 jest mniejsza od 729.
jest mniejsza od 729.
Iloczyn piątego i jedenastego wyrazu ciągu geometrycznego o wyrazach dodatnich jest równy 4. Oblicz iloczyn piętnastu początkowych kolejnych wyrazów tego ciągu.

