W ciągu geometrycznym 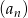 dane są iloraz
dane są iloraz 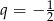 oraz suma
oraz suma
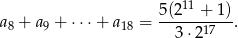
Oblicz 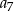 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W ciągu geometrycznym 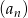 dane są iloraz
dane są iloraz 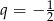 oraz suma
oraz suma
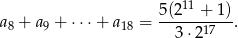
Oblicz 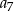 .
.
Uzasadnij, że jeśli miary kątów wewnętrznych pewnego trójkąta są kolejnymi wyrazami ciągu arytmetycznego, to jeden z tych kątów ma miarę 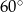 .
.
Ciąg 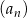 jest ciągiem arytmetycznym o różnicy 2 i czwartym wyrazie równym
jest ciągiem arytmetycznym o różnicy 2 i czwartym wyrazie równym 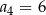 . Ciąg
. Ciąg 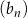 dla dowolnego
dla dowolnego 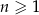 spełnia warunek
spełnia warunek 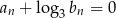 . Oblicz granicę
. Oblicz granicę
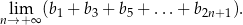
Dla jakich 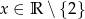 , liczby
, liczby 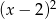 ,
, 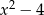 ,
, 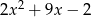 w podanej kolejności tworzą ciąg geometryczny? Dla znalezionej wartości
w podanej kolejności tworzą ciąg geometryczny? Dla znalezionej wartości  wyznacz ciąg i jego iloraz.
wyznacz ciąg i jego iloraz.
Miary kątów wielokąta tworzą ciąg arytmetyczny, którego różnica jest równa 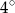 . Największy kąt ma miarę
. Największy kąt ma miarę 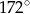 .
.
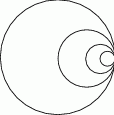
Dane jest koło o promieniu  . W tym kole narysowano koło styczne wewnętrznie o średnicy
. W tym kole narysowano koło styczne wewnętrznie o średnicy  , w narysowanym kole znów narysowano koło styczne wewnętrznie o średnicy
, w narysowanym kole znów narysowano koło styczne wewnętrznie o średnicy 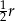 itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę pól wszystkich narysowanych kół.
itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę pól wszystkich narysowanych kół.
W nieskończonym rosnącym ciągu geometrycznym 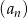 o wyrazach dodatnich, określonym dla
o wyrazach dodatnich, określonym dla 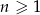 , stosunek średniej geometrycznej trzech pierwszych wyrazów do średniej arytmetycznej tych wyrazów jest równy
, stosunek średniej geometrycznej trzech pierwszych wyrazów do średniej arytmetycznej tych wyrazów jest równy 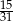 , a suma czterech pierwszych wyrazów tego ciągu jest równa 468. Wyrazy
, a suma czterech pierwszych wyrazów tego ciągu jest równa 468. Wyrazy 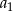 i
i 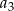 ciągu
ciągu 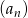 , są odpowiednio pierwszym i trzecim wyrazem ciągu arytmetycznego
, są odpowiednio pierwszym i trzecim wyrazem ciągu arytmetycznego 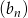 . Oblicz sumę 10 początkowych wyrazów ciągu
. Oblicz sumę 10 początkowych wyrazów ciągu 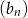 .
.
Uwaga: średnia geometryczna liczb 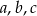 jest równa
jest równa 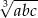 .
.
Dla każdego 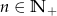 wyrazy ciągu
wyrazy ciągu 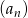 spełniają dwa warunki
spełniają dwa warunki 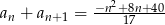 i
i 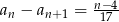 . Oblicz, które wyrazy tego ciągu są dodatnie.
. Oblicz, które wyrazy tego ciągu są dodatnie.
Liczby 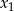 i
i 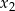 są pierwiastkami równania
są pierwiastkami równania 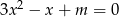 , gdzie
, gdzie 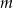 jest pewną ujemną liczbą rzeczywistą. Ciąg
jest pewną ujemną liczbą rzeczywistą. Ciąg 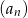 określony jest wzorem
określony jest wzorem 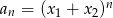 . Oblicz sumę wyrazów tego ciągu.
. Oblicz sumę wyrazów tego ciągu.
Ciąg 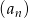 , gdzie
, gdzie 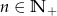 , określony jest następująco:
, określony jest następująco:
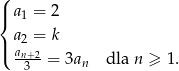
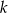 , jeżeli ciąg
, jeżeli ciąg 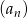 jest ciągiem geometrycznym, w którym suma sześciu początkowych wyrazów jest równa
jest ciągiem geometrycznym, w którym suma sześciu początkowych wyrazów jest równa 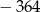 .
.  suma
suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 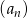 jest równa 9842.
jest równa 9842.Dwie dowolne liczby rzeczywiste i ich suma tworzą ciąg arytmetyczny (niekoniecznie w takiej kolejności). Wykaż, że jedna z tych liczb jest dwukrotnością drugiej liczby lub, że liczby te są liczbami przeciwnymi.
W ciągu arytmetycznym mamy dane 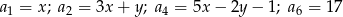 . Niech
. Niech 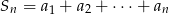 . Dla jakich
. Dla jakich  zachodzi równość
zachodzi równość 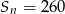 ?
?
Ciąg 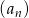 jest określony rekurencyjnie w następujący sposób
jest określony rekurencyjnie w następujący sposób
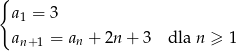
Oblicz ile wyrazów tego ciągu jest mniejszych niż 2018.
Oblicz granicę 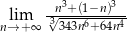 .
.
Wartości funkcji 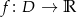 spełniają dla każdego
spełniają dla każdego 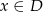 następujące równanie
następujące równanie
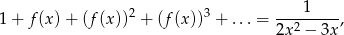
gdzie lewa strona równania jest sumą szeregu geometrycznego.
 .
. 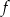 .
.W ciągu arytmetycznym wyraz pierwszy jest równy 1, a ostatni 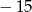 . Oblicz sumę wyrazów tego ciągu, jeśli wiadomo że drugi, trzeci i szósty są kolejnymi wyrazami ciągu geometrycznego.
. Oblicz sumę wyrazów tego ciągu, jeśli wiadomo że drugi, trzeci i szósty są kolejnymi wyrazami ciągu geometrycznego.
Dany jest nieskończony ciąg geometryczny 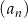 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 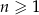 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 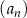 jest równa 7, a suma
jest równa 7, a suma 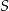 wszystkich wyrazów tego ciągu jest równa 8. Wyznacz wszystkie wartości
wszystkich wyrazów tego ciągu jest równa 8. Wyznacz wszystkie wartości  , dla których spełniona jest nierówność
, dla których spełniona jest nierówność
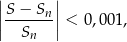
gdzie 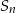 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 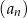 .
.
Dany jest nieskończony ciąg geometryczny 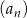 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 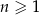 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 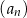 jest równa 26, a suma
jest równa 26, a suma  wszystkich wyrazów tego ciągu jest równa 27. Wyznacz wszystkie wartości
wszystkich wyrazów tego ciągu jest równa 27. Wyznacz wszystkie wartości  , dla których spełniona jest nierówność
, dla których spełniona jest nierówność
gdzie  oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu  .
.
Zbadaj, czy ciąg 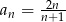 jest arytmetyczny.
jest arytmetyczny.
Na wykresie funkcji 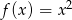 wybrano trzy różne punkty, których odcięte są kolejnymi wyrazami ciągu arytmetycznego, a rzędne kolejnymi wyrazami ciągu geometrycznego. Wykaż, że odcięta co najmniej jednego z tych punktów jest liczbą niewymierną.
wybrano trzy różne punkty, których odcięte są kolejnymi wyrazami ciągu arytmetycznego, a rzędne kolejnymi wyrazami ciągu geometrycznego. Wykaż, że odcięta co najmniej jednego z tych punktów jest liczbą niewymierną.
Wykaż, że dla każdej liczby naturalnej  , liczby
, liczby 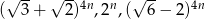 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
