Oblicz granicę 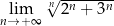 .
.
/Szkoła średnia/Ciągi
Oblicz granicę 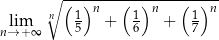 .
.
Oblicz granicę 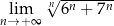 .
.
Oblicz granicę 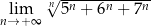 .
.
Wykaż, że jeżeli ciąg 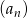 jest arytmetyczny, to ciąg
jest arytmetyczny, to ciąg 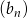 określony wzorem
określony wzorem 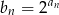 jest geometryczny.
jest geometryczny.
W ciągu geometrycznym 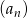 dane są iloraz
dane są iloraz 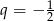 oraz suma
oraz suma
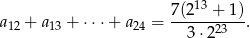
Oblicz  , dla którego ciąg
, dla którego ciąg 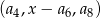 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Wyznacz liczbę  , tak aby liczby dodatnie:
, tak aby liczby dodatnie: 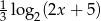 ,
, 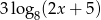 ,
, 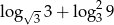 tworzyły ciąg geometryczny.
tworzyły ciąg geometryczny.
Liczby 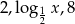 są (w podanej kolejności) wyrazami ciągu arytmetycznego. Wyznacz
są (w podanej kolejności) wyrazami ciągu arytmetycznego. Wyznacz  .
.
Dane są dwa skończone ciągi geometryczne 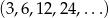 i
i 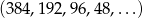 o tej samej liczbie wyrazów. Znajdź liczbę wyrazów każdego z tych ciągów wiedząc, że łączna suma ich wyrazów wynosi 1530.
o tej samej liczbie wyrazów. Znajdź liczbę wyrazów każdego z tych ciągów wiedząc, że łączna suma ich wyrazów wynosi 1530.
Liczba  jest pierwszym wyrazem ciągu geometrycznego
jest pierwszym wyrazem ciągu geometrycznego 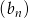 , którego iloraz jest równy
, którego iloraz jest równy 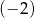 . Pierwszy wyraz ciągu arytmetycznego
. Pierwszy wyraz ciągu arytmetycznego 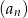 jest taki sam jak pierwszy wyraz ciągu
jest taki sam jak pierwszy wyraz ciągu 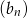 . Suma siedmiu początkowych wyrazów ciągu
. Suma siedmiu początkowych wyrazów ciągu 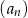 jest równa sumie siedmiu początkowych wyrazów ciągu
jest równa sumie siedmiu początkowych wyrazów ciągu 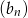 . Oblicz różnicę ciągu arytmetycznego
. Oblicz różnicę ciągu arytmetycznego 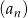 .
.
Konstruujemy ciąg trójkątów równobocznych 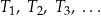 następująco:
następująco:
-
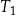 jest trójkątem równobocznym o polu 1.
jest trójkątem równobocznym o polu 1. -
dla każdego
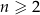 , trójkąt
, trójkąt 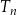 ma wierzchołki na trzech różnych bokach trójkąta
ma wierzchołki na trzech różnych bokach trójkąta 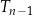 i każdy z wierzchołków trójkąta
i każdy z wierzchołków trójkąta 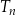 dzieli odpowiedni bok trójkąta
dzieli odpowiedni bok trójkąta 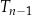 w stosunku 1 : 2.
w stosunku 1 : 2.
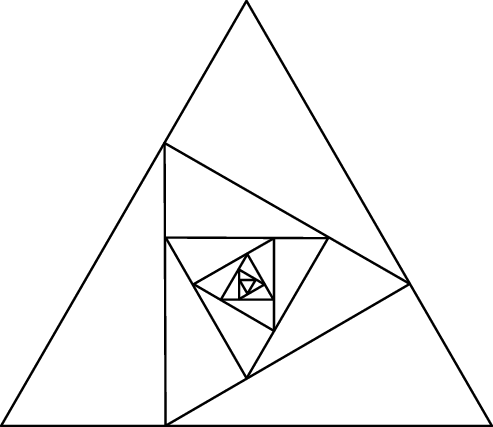
Oblicz sumę pól wszystkich trójkątów 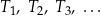 .
.
Ciąg 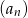 określony jest przez warunki
określony jest przez warunki 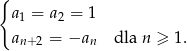
- Wypisz 6 początkowych wyrazów ciągu
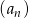 .
. - Oblicz sumę 20 początkowych wyrazów ciągu
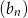 danego wzorem
danego wzorem 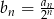 .
.
Trzywyrazowy ciąg 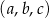 o wyrazach dodatnich jest arytmetyczny, natomiast ciąg
o wyrazach dodatnich jest arytmetyczny, natomiast ciąg
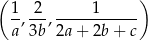
jest geometryczny. Oblicz iloraz ciągu geometrycznego.
Trzywyrazowy ciąg 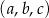 o wyrazach dodatnich jest arytmetyczny, natomiast ciąg
o wyrazach dodatnich jest arytmetyczny, natomiast ciąg
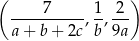
jest geometryczny. Oblicz iloraz ciągu geometrycznego.
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 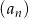 wyraża się wzorem
wyraża się wzorem 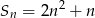 dla
dla 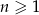 .
.
- Oblicz sumę 50 początkowych wyrazów tego ciągu o numerach parzystych:
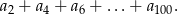
- Oblicz
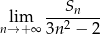
Oblicz pierwszy wyraz i iloraz ciągu geometrycznego wiedząc, że trzeci wyraz jest równy 18, a szósty 486.
Ciąg 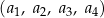 jest arytmetyczny. Suma pierwszego i drugiego wyrazu jest o 12 większa od sumy trzeciego i czwartego wyrazu tego ciągu. Oblicz różnicę tego ciągu.
jest arytmetyczny. Suma pierwszego i drugiego wyrazu jest o 12 większa od sumy trzeciego i czwartego wyrazu tego ciągu. Oblicz różnicę tego ciągu.
Ciąg 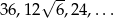 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.
- Oblicz iloraz
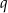 tego ciągu.
tego ciągu. - Zapisz
 -ty wyraz tego ciągu w postaci
-ty wyraz tego ciągu w postaci 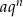
- Oblicz sumę ośmiu początkowych wyrazów tego ciągu.
Ciąg 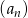 dany jest wzorem
dany jest wzorem 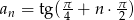 . Oblicz sumę
. Oblicz sumę 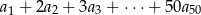 .
.
Ciąg 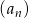 , gdzie
, gdzie 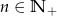 , jest nieskończonym ciągiem arytmetycznym o różnicy 2, w którym pierwszy wyraz jest równy
, jest nieskończonym ciągiem arytmetycznym o różnicy 2, w którym pierwszy wyraz jest równy 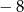 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 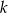 , dla których trzywyrazowy ciąg
, dla których trzywyrazowy ciąg 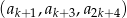 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.
Ciąg 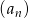 , gdzie
, gdzie 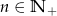 , jest nieskończonym ciągiem arytmetycznym o różnicy 2, w którym pierwszy wyraz jest równy
, jest nieskończonym ciągiem arytmetycznym o różnicy 2, w którym pierwszy wyraz jest równy 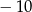 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 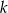 , dla których trzywyrazowy ciąg
, dla których trzywyrazowy ciąg 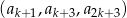 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.
Ciąg 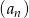 określony dla
określony dla 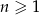 jest rosnący, ma wszystkie wyrazy ujemne oraz spełnia warunki
jest rosnący, ma wszystkie wyrazy ujemne oraz spełnia warunki
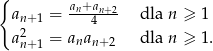
Oblicz iloraz 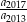 .
.
Dany jest ciąg określony rekurencyjnie
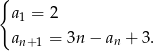
Wyznacz liczby całkowite 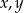 tak, aby ciąg
tak, aby ciąg 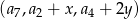 był ciągiem arytmetycznym, natomiast ciąg
był ciągiem arytmetycznym, natomiast ciąg 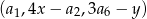 był ciągiem geometrycznym.
był ciągiem geometrycznym.
Oblicz sumę pierwszych 14 wyrazów ciągu arytmetycznego 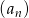 jeżeli
jeżeli 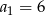 oraz
oraz 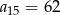 .
.
W ciągu arytmetycznym 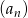 pierwszy wyraz
pierwszy wyraz 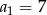 , a czwarty wyraz
, a czwarty wyraz 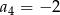 . Oblicz sumę osiemnastu początkowych wyrazów tego ciągu.
. Oblicz sumę osiemnastu początkowych wyrazów tego ciągu.
W ciągu arytmetycznym 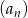 pierwszy wyraz
pierwszy wyraz 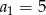 , a czwarty wyraz
, a czwarty wyraz 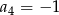 . Oblicz sumę dwudziestu początkowych wyrazów tego ciągu.
. Oblicz sumę dwudziestu początkowych wyrazów tego ciągu.
Pierwszy wyraz ciągu arytmetycznego jest równy 4, piąty wyraz tego ciągu jest równy 16. Oblicz sumę siedmiu początkowych wyrazów tego ciągu.
Oblicz sumę pierwszych 4 wyrazów ciągu arytmetycznego 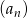 jeżeli
jeżeli 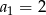 oraz
oraz 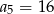
W ciągu arytmetycznym 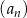 , określonym dla każdej liczby naturalnej
, określonym dla każdej liczby naturalnej 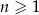 ,
, 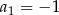 i
i 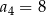 . Oblicz sumę stu początkowych kolejnych wyrazów tego ciągu.
. Oblicz sumę stu początkowych kolejnych wyrazów tego ciągu.
Oblicz sumę pierwszych 8 wyrazów ciągu arytmetycznego 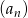 jeżeli
jeżeli 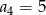 oraz
oraz 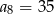 .
.
Pierwszy wyraz ciągu arytmetycznego jest równy 2, czwarty wyraz tego ciągu jest równy 14. Oblicz sumę sześciu początkowych wyrazów tego ciągu.
Oblicz sumę pierwszych 10 wyrazów ciągu arytmetycznego 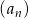 jeżeli
jeżeli 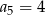 oraz
oraz 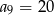 .
.
Pierwszy wyraz ciągu arytmetycznego jest równy 3, czwarty wyraz tego ciągu jest równy 15. Oblicz sumę sześciu początkowych wyrazów tego ciągu.
Oblicz granicę 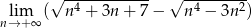 .
.
Oblicz granicę 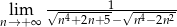 .
.
Oblicz granicę 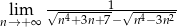 .
.
Oblicz granicę 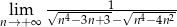 .
.
Oblicz granicę 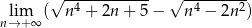 .
.
Oblicz granicę 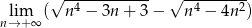 .
.

