O liczbach 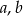 i
i  wiadomo, że tworzą ciąg arytmetyczny oraz ich suma wynosi
wiadomo, że tworzą ciąg arytmetyczny oraz ich suma wynosi 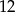 . Wyznacz największą możliwą wartość wyrażenia
. Wyznacz największą możliwą wartość wyrażenia 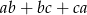 . Dla jakich liczb
. Dla jakich liczb 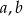 i
i  wartość ta jest osiągana.
wartość ta jest osiągana.
/Szkoła średnia/Ciągi
Wyznacz największy wyraz ciągu 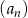 danego wzorem
danego wzorem 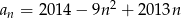 , dla
, dla 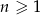 .
.
Ciągiem Fibonacciego nazywamy ciąg, którego dwa pierwsze wyrazy są równe 1, a każdy kolejny jest sumą dwóch poprzednich. Jaką liczbą, parzystą czy nieparzystą, jest 528 wyraz ciągu Fibonacciego? Odpowiedź uzasadnij.
Oblicz miary kątów trójkąta, w którym długości boków tworzą ciąg geometryczny, a miary kątów tworzą ciąg arytmetyczny.
Wykaż, że dla każdego 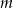 ciąg
ciąg 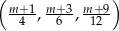 jest arytmetyczny.
jest arytmetyczny.
Wykaż, że dla każdego  ciąg
ciąg 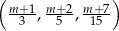 jest arytmetyczny.
jest arytmetyczny.
Długości boków trójkąta są kolejnymi wyrazami ciągu arytmetycznego. Obwód trójkąta jest równy 33, a cosinus największego kąta jest równy  . Oblicz promień okręgu opisanego na tym trójkącie.
. Oblicz promień okręgu opisanego na tym trójkącie.
Na płaszczyźnie dany jest nieskończony ciąg 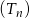 , dla
, dla 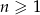 , równoramiennych trójkątów prostokątnych. Pole trójkąta
, równoramiennych trójkątów prostokątnych. Pole trójkąta 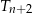 jest dwa razy mniejsze od pola trójkąta
jest dwa razy mniejsze od pola trójkąta 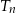 dla
dla 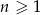 . Uzasadnij, że suma pól trójkątów
. Uzasadnij, że suma pól trójkątów 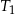 i
i 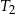 jest równa sumie pól wszystkich pozostałych trójkątów.
jest równa sumie pól wszystkich pozostałych trójkątów.
Na płaszczyźnie dany jest nieskończony ciąg 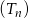 , dla
, dla 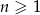 , trójkątów równobocznych. Pole trójkąta
, trójkątów równobocznych. Pole trójkąta 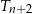 jest dwa razy mniejsze od pola trójkąta
jest dwa razy mniejsze od pola trójkąta 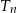 dla
dla 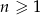 . Uzasadnij, że suma pól trójkątów
. Uzasadnij, że suma pól trójkątów 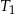 i
i 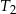 jest równa sumie pól wszystkich pozostałych trójkątów.
jest równa sumie pól wszystkich pozostałych trójkątów.
Sprawdź, czy liczby 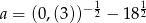 ,
, 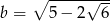 ,
, 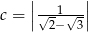 są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
Oblicz granicę
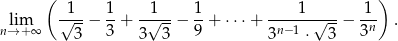
Oblicz granicę
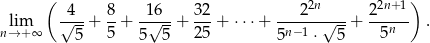
Ciąg 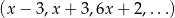 jest nieskończonym ciągiem geometrycznym o wyrazach dodatnich. Oblicz iloraz tego ciągu i uzasadnij, że
jest nieskończonym ciągiem geometrycznym o wyrazach dodatnich. Oblicz iloraz tego ciągu i uzasadnij, że 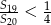 , gdzie
, gdzie 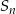 oznacza sumę
oznacza sumę  początkowych wyrazów tego ciągu.
początkowych wyrazów tego ciągu.
Jedno z rozwiązań równania 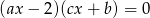 jest równe 6. Ciąg
jest równe 6. Ciąg 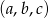 jest ciągiem arytmetycznym, w którym pierwszy wyraz jest o 8 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
jest ciągiem arytmetycznym, w którym pierwszy wyraz jest o 8 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
Czwarty wyraz ciągu arytmetycznego jest równy 6. Oblicz sumę siedmiu początkowych wyrazów tego ciągu.
Dany jest nieskończony ciąg geometryczny 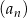 określony dla
określony dla 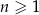 , w którym
, w którym 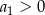 . Suma
. Suma 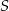 wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność
wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność 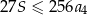 . Wyznacz iloraz tego ciągu.
. Wyznacz iloraz tego ciągu.
W malejącym ciągu arytmetycznym 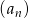 spełnione są warunki
spełnione są warunki 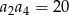 oraz
oraz 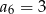 . Wyznacz sumę 10 początkowych wyrazów tego ciągu.
. Wyznacz sumę 10 początkowych wyrazów tego ciągu.
Rosnące, trzywyrazowe ciągi arytmetyczny i geometryczny mają pierwsze wyrazy równe 9. Trzecie wyrazy tych ciągów są także równe. Drugi wyraz ciągu arytmetycznego jest o 2 większy od drugiego wyrazu ciągu geometrycznego. Wyznacz te ciągi.
Pierwszy, trzeci i jedenasty wyraz ciągu arytmetycznego o różnicy 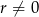 są kolejnymi wyrazami ciągu geometrycznego o ilorazie
są kolejnymi wyrazami ciągu geometrycznego o ilorazie 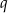 . Dla jakich wartości parametru
. Dla jakich wartości parametru 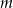 funkcja
funkcja 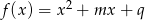 osiąga minimum większe od
osiąga minimum większe od 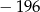 ?
?
Trzy książki, których ceny tworzą ciąg geometryczny zakupiono płacąc łącznie 76 zł. Najdroższa z nich kosztowała o 4 zł mniej niż dwie pozostałe razem. Ile kosztowała każda książka?
Suma trzech początkowych wyrazów rosnącego ciągu geometrycznego 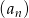 , określonego dla
, określonego dla 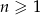 , jest równa
, jest równa 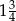 . Te same liczby stanowią pierwszy, drugi oraz czwarty wyraz ciągu arytmetycznego
. Te same liczby stanowią pierwszy, drugi oraz czwarty wyraz ciągu arytmetycznego 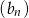 ,
, 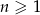 . Wyznacz wzór ciągu
. Wyznacz wzór ciągu 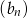 .
.

