Suma trzech liczb tworzących ciąg geometryczny jest równa 26, a ich iloczyn jest równy 216. Wyznacz ten ciąg.
/Szkoła średnia/Ciągi
Suma trzech liczb tworzących ciąg geometryczny jest równa 63, a ich iloczyn jest równy 5832. Wyznacz ten ciąg.
Wyznacz trzywyrazowy ciąg geometryczny, w którym suma trzech kolejnych wyrazów jest równa 84, a ich iloczyn jest równy 13824.
Trzy liczby dodatnie tworzą rosnący ciąg geometryczny o sumie równej 62. Suma logarytmów dziesiętnych tych liczb jest równa 3. Wyznacz te liczby.
Udowodnij że w ciągu geometrycznym o parzystej liczbie wyrazów stosunek sumy wyrazów stojących na miejscach parzystych do sumy wyrazów stojących na miejscach nieparzystych jest równy ilorazowi tego ciągu.
Trzywyrazowy ciąg geometryczny jest rosnący. Iloczyn wszystkich wyrazów tego ciągu jest równy -8, a iloraz pierwszego wyrazu przez trzeci wynosi 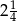 . Wyznacz ten ciąg.
. Wyznacz ten ciąg.
W ciągu arytmetycznym 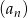 , dla
, dla 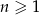 , dane są
, dane są 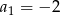 oraz różnica
oraz różnica 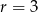 . Oblicz największe
. Oblicz największe  takie, że
takie, że 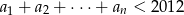 .
.
W ciągu arytmetycznym 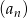 , dla
, dla 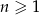 , dane są
, dane są 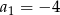 oraz różnica
oraz różnica 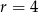 . Wyznacz największe
. Wyznacz największe  takie, że
takie, że 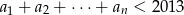 .
.
Ciąg 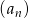 jest określony wzorem
jest określony wzorem
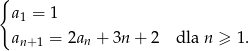
Oblicz średnią arytmetyczną liczb 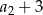 i
i 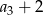 .
.
Miary kątów trójkąta prostokątnego tworzą ciąg arytmetyczny. Jeśli trójkąt ten będziemy obracać wokół dłuższej przyprostokątnej, to otrzymamy stożek, którego pole powierzchni bocznej wynosi 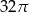 . Oblicz długości boków tego trójkąta.
. Oblicz długości boków tego trójkąta.
Określ wzorem rekurencyjnym ciąg którego pierwszy i drugi wyraz jest równy 3, a każdy następny jest iloczynem dwóch poprzednich.
Iloczyn pierwszego i szóstego wyrazu malejącego ciągu arytmetycznego o wyrazach całkowitych jest równy 100. Przy dzieleniu wyrazu drugiego przez wyraz szósty otrzymujemy 3 i resztę 2. Oblicz, o ile jest mniejsza suma dwustu początkowych wyrazów o numerach parzystych od sumy dwustu początkowych wyrazów tego ciągu o numerach nieparzystych.
W graniastosłupie prawidłowym trójkątnym wysokość podstawy, krawędź podstawy i wysokość graniastosłupa tworzą ciąg geometryczny. Oblicz długość krawędzi podstawy graniastosłupa wiedząc, że jego objętość jest równa 108.
Dany jest ciąg arytmetyczny 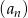 o różnicy
o różnicy 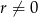 i pierwszym wyrazie
i pierwszym wyrazie 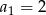 . Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.
. Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.
Liczby 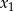 i
i 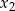 są pierwiastkami równania
są pierwiastkami równania 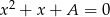 , a liczby
, a liczby 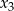 i
i 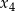 są pierwiastkami równania
są pierwiastkami równania 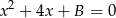 . Wiadomo, że ciąg
. Wiadomo, że ciąg 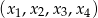 jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz
jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz 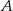 i
i 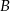 .
.
Uzasadnij, że ciąg określony wzorem 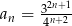 jest ciągiem geometrycznym. Wyznacz iloraz osiemnastego wyrazu tego ciągu przez wyraz 16.
jest ciągiem geometrycznym. Wyznacz iloraz osiemnastego wyrazu tego ciągu przez wyraz 16.
W ciągu arytmetycznym 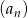 o różnicy
o różnicy 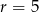 dane są:
dane są: 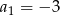 i
i 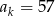 . Wyznacz liczbę
. Wyznacz liczbę 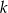 oraz oblicz sumę
oraz oblicz sumę 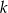 początkowych wyrazów ciągu
początkowych wyrazów ciągu 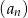
Długości boków trójkąta tworzą ciąg geometryczny. Jaki warunek spełniać musi iloraz tego ciągu?
Długości boków trójkąta tworzą trzy kolejne wyrazy ciągu arytmetycznego o różnicy 1. Oblicz długości boków tego trójkąta, jeśli jego pole wynosi 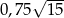 .
.
Suma wszystkich wyrazów ciągu danego wzorem 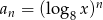 , gdzie
, gdzie 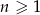 jest równa
jest równa 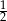 . Oblicz
. Oblicz  .
.
O ciągu 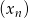 dla
dla 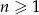 wiadomo, że:
wiadomo, że:
- ciąg
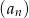 określony wzorem
określony wzorem 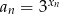 dla
dla 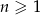 jest geometryczny o ilorazie
jest geometryczny o ilorazie 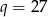 .
. 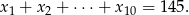
Oblicz 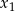 .
.
Ciąg 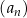 jest określony wzorem
jest określony wzorem
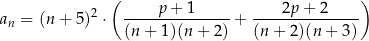
dla każdej liczby naturalnej 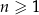 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 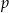 , dla których granica ciągu
, dla których granica ciągu 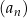 jest równa 12.
jest równa 12.
Długości boków trójkąta są kolejnymi wyrazami rosnącego ciągu geometrycznego o ilorazie 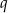 , a cosinus jednego z jego kątów jest równy
, a cosinus jednego z jego kątów jest równy 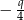 .
.
- Wyznacz
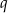 .
. - Wiedząc, że promień okręgu opisanego na tym trójkącie ma długość
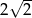 , oblicz pole tego trójkąta.
, oblicz pole tego trójkąta.
O liczbach 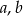 i
i  wiadomo, że tworzą ciąg arytmetyczny oraz ich suma wynosi
wiadomo, że tworzą ciąg arytmetyczny oraz ich suma wynosi 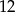 . Wyznacz największą możliwą wartość wyrażenia
. Wyznacz największą możliwą wartość wyrażenia 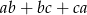 . Dla jakich liczb
. Dla jakich liczb 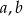 i
i  wartość ta jest osiągana.
wartość ta jest osiągana.

