Dany jest ciąg 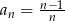 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 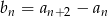 , gdzie
, gdzie 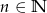 .
.
/Szkoła średnia/Ciągi
Dany jest ciąg 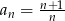 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 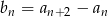 , gdzie
, gdzie 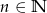 .
.
W nieskończonym ciągu arytmetycznym 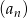 , określonym dla
, określonym dla 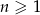 , suma jedenastu początkowych wyrazów tego ciągu jest równa 187. Średnia arytmetyczna pierwszego, trzeciego i dziewiątego wyrazu tego ciągu, jest równa 12. Wyrazy
, suma jedenastu początkowych wyrazów tego ciągu jest równa 187. Średnia arytmetyczna pierwszego, trzeciego i dziewiątego wyrazu tego ciągu, jest równa 12. Wyrazy 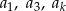 ciągu
ciągu 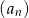 , w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny
, w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny 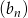 . Oblicz
. Oblicz 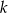 .
.
W nieskończonym ciągu arytmetycznym 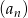 , określonym dla
, określonym dla 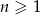 , suma dziewięciu początkowych wyrazów jest równa 171. Średnia arytmetyczna pierwszego, trzeciego i ósmego wyrazu tego ciągu, jest równa 15. Wyrazy
, suma dziewięciu początkowych wyrazów jest równa 171. Średnia arytmetyczna pierwszego, trzeciego i ósmego wyrazu tego ciągu, jest równa 15. Wyrazy 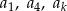 ciągu
ciągu 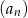 , w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny
, w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny 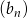 . Oblicz
. Oblicz 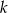 .
.
Liczbę 255 przedstaw jako sumę czterech całkowitych składników będących kolejnymi wyrazami ciągu geometrycznego tak, aby trzeci wyraz był o 45 większy od wyrazu pierwszego.
W 10-wyrazowym ciągu arytmetycznym suma wyrazów o numerach nieparzystych jest równa 35. Oblicz piąty wyraz tego ciągu.
Oblicz sumę nieskończonego ciągu geometrycznego 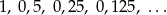
Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny. Najkrótszy bok ma długość 6 cm. Oblicz
- pole tego trójkata;
- długość promienia okręgu opisanego na trójkącie;
- długość promienia okręgu wpisanego w trójkąt.
Dany jest nieskończony ciąg geometryczny
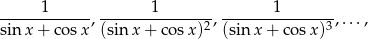
gdzie 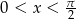 .
.
- Wykaż, że dany ciąg jest malejący.
- Wyznacz sumę
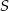 wszystkich wyrazów tego ciągu.
wszystkich wyrazów tego ciągu. - Wiedząc, że suma
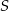 wszystkich wyrazów tego ciągu wynosi
wszystkich wyrazów tego ciągu wynosi 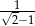 , oblicz
, oblicz  .
.
Współczynniki 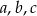 funkcji kwadratowej
funkcji kwadratowej 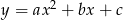 w podanej kolejności tworzą ciąg arytmetyczny. Jednym z miejsc zerowych jest 2. Punkt o współrzędnych
w podanej kolejności tworzą ciąg arytmetyczny. Jednym z miejsc zerowych jest 2. Punkt o współrzędnych 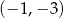 należy do wykresu tej funkcji. Znajdź drugie miejsce zerowe oraz wartości współczynników
należy do wykresu tej funkcji. Znajdź drugie miejsce zerowe oraz wartości współczynników 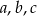 .
.
Współczynniki 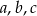 funkcji kwadratowej
funkcji kwadratowej 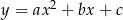 w podanej kolejności tworzą ciąg arytmetyczny. Jednym z miejsc zerowych tej funkcji jest
w podanej kolejności tworzą ciąg arytmetyczny. Jednym z miejsc zerowych tej funkcji jest 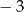 . Punkt o współrzędnych
. Punkt o współrzędnych 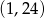 należy do wykresu funkcji. Znajdź drugie miejsce zerowe oraz wartości współczynników
należy do wykresu funkcji. Znajdź drugie miejsce zerowe oraz wartości współczynników 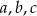 .
.
Oblicz granicę 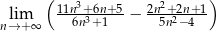 .
.
Oblicz granicę 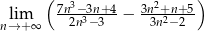 .
.
Oblicz granicę 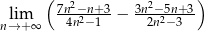 .
.
Oblicz granicę 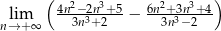 .
.
Oblicz granicę 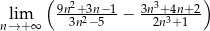 .
.
Oblicz granicę 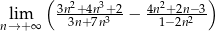 .
.
Oblicz granicę 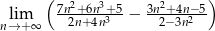 .
.
Oblicz granicę 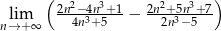 .
.
Oblicz granicę 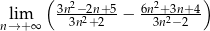 .
.
Oblicz granicę 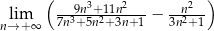 .
.
Siódmy wyraz ciągu geometrycznego 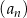 , określonego dla
, określonego dla 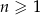 , jest równy 6, a suma jego sześciu początkowych wyrazów jest równa 756. Iloraz
, jest równy 6, a suma jego sześciu początkowych wyrazów jest równa 756. Iloraz 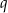 tego ciągu spełnia warunek:
tego ciągu spełnia warunek: 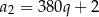 . Oblicz pierwszy wyraz oraz iloraz tego ciągu.
. Oblicz pierwszy wyraz oraz iloraz tego ciągu.
Ciąg 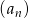 określony jest wzorem
określony jest wzorem 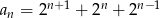 .
.
- Oblicz pierwszy i trzeci wyraz tego ciągu.
- Uzasadnij, korzystając z definicji ciągu geometrycznego, że ciąg
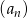 jest geometryczny.
jest geometryczny.
Oblicz granicę 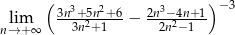 .
.
Oblicz granicę 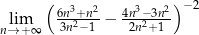 .
.
Wykaż, że jeżeli żadne dwie spośród liczb 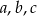 nie są równe oraz liczby
nie są równe oraz liczby 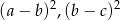 i
i 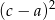 tworzą ciąg arytmetyczny, to liczby
tworzą ciąg arytmetyczny, to liczby 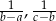 i
i 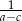 również tworzą ciąg arytmetyczny.
również tworzą ciąg arytmetyczny.
Wartość pewnej frezarki maleje z roku na rok. Wartości tej frezarki w kolejnych latach tworzą ciąg arytmetyczny. Oblicz czas, w ciągu którego frezarka całkowicie straci wartość (zamortyzuje się), jeżeli wiadomo, że po 15 latach użytkowania jej wartość była 3 razy większa niż jej wartość po 25 latach.
Oblicz granicę 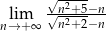 .
.
Oblicz granicę 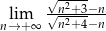 .
.
Oblicz granicę 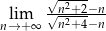 .
.
Oblicz granicę 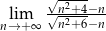 .
.
Oblicz granicę 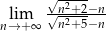 .
.
Oblicz granicę 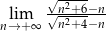 .
.
Oblicz granicę 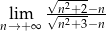 .
.
Oblicz granicę 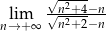 .
.
Oblicz granicę 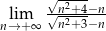 .
.
Oblicz granicę 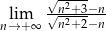 .
.
Wiedząc, że dla sum częściowych pewnego ciągu geometrycznego o wyrazach dodatnich prawdziwa jest równość 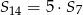 , oblicz iloraz tego ciągu.
, oblicz iloraz tego ciągu.
Niech 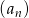 oznacza ciąg geometryczny o wyrazach dodatnich, natomiast
oznacza ciąg geometryczny o wyrazach dodatnich, natomiast 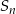 niech oznacza sumę
niech oznacza sumę  początkowych wyrazów tego ciągu. Wiedząc, że
początkowych wyrazów tego ciągu. Wiedząc, że 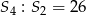 , oblicz
, oblicz 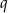 .
.
Liczby 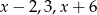 są w podanej kolejności pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Oblicz  .
.
Liczby 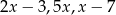 są trzema początkowymi wyrazami ciągu arytmetycznego. Wyznacz liczbę
są trzema początkowymi wyrazami ciągu arytmetycznego. Wyznacz liczbę  .
.
Ciąg 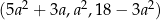 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz  .
.
Ciąg 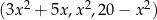 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz  .
.
Liczby 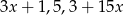 są w podanej kolejności pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Oblicz  .
.
Trzywyrazowy ciąg 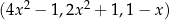 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz  .
.
Liczby 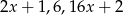 są w podanej kolejności pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Oblicz  .
.
Suma drugiego, czwartego i szóstego wyrazu ciągu arytmetycznego jest równa 42, zaś suma kwadratów wyrazów drugiego i trzeciego jest równa 185. Wyznacz pierwszy wyraz i różnicę tego ciągu.
Suma wszystkich wyrazów nieskończonego ciągu geometrycznego jest równa 3, a suma sześcianów wszystkich jego wyrazów jest równa 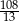 . Oblicz pierwszy wyraz tego ciągu i jego iloraz.
. Oblicz pierwszy wyraz tego ciągu i jego iloraz.
Oblicz granicę ciągu 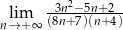 .
.
Oblicz granicę ciągu 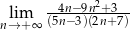 .
.
Oblicz granicę ciągu 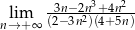 .
.
Oblicz granicę ciągu 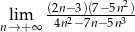 .
.
Oblicz granicę ciągu 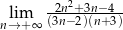 .
.
Oblicz granicę ciągu 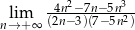 .
.
Oblicz granicę ciągu 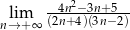 .
.
Oblicz granicę ciągu 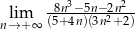 .
.
Oblicz granicę ciągu 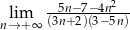 .
.
Oblicz granicę ciągu 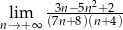 .
.
Oblicz granicę ciągu 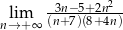 .
.
Oblicz granicę ciągu 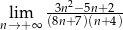 .
.
Oblicz granicę ciągu 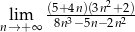 .
.
Oblicz granicę ciągu 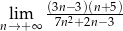 .
.
Oblicz granicę ciągu 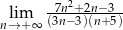 .
.
Oblicz granicę ciągu 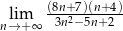 .
.
Oblicz granicę ciągu 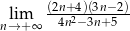 .
.

