Oblicz granicę ciągu 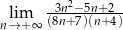 .
.
/Szkoła średnia/Ciągi
Oblicz granicę ciągu 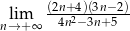 .
.
Oblicz granicę ciągu 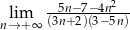 .
.
Oblicz granicę ciągu 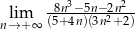 .
.
Oblicz granicę ciągu 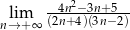 .
.
Oblicz granicę ciągu 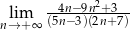 .
.
Oblicz granicę ciągu 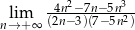 .
.
Oblicz granicę ciągu 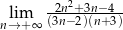 .
.
Oblicz granicę ciągu 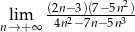 .
.
Oblicz granicę ciągu 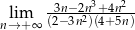 .
.
Oblicz granicę ciągu 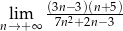 .
.
Oblicz granicę ciągu 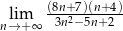 .
.
Oblicz granicę ciągu 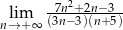 .
.
Oblicz granicę ciągu 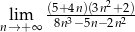 .
.
Oblicz granicę ciągu 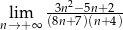 .
.
Oblicz granicę ciągu 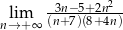 .
.
Oblicz granicę ciągu 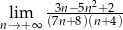 .
.
Dany jest ciąg arytmetyczny 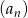 dla
dla 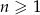 , w którym
, w którym 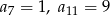 .
.
- Oblicz pierwszy wyraz
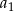 i różnicę
i różnicę  ciągu
ciągu 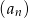 .
. - Sprawdź, czy ciąg
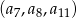 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 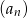 miała wartość najmniejszą.
miała wartość najmniejszą.
Podaj wzór na wyraz ogólny ciągu 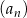 określonego w następujący sposób:
określonego w następujący sposób: 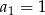 oraz ciąg
oraz ciąg 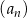 jest ciągiem kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 1.
jest ciągiem kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 1.
Pierwszy, trzeci i trzynasty wyraz ciągu arytmetycznego 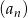 ,
, 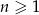 są kolejnymi wyrazami ciągu geometrycznego. Piąty wyraz ciągu
są kolejnymi wyrazami ciągu geometrycznego. Piąty wyraz ciągu 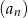 jest równy 27. Wyznacz wzór ciągu
jest równy 27. Wyznacz wzór ciągu 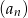 wiedząc, że nie jest to ciąg stały.
wiedząc, że nie jest to ciąg stały.
Dany jest nieskończony rosnący ciąg arytmetyczny 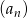 , dla
, dla 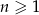 taki, że
taki, że 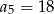 . Wyrazy
. Wyrazy 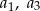 oraz
oraz 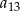 tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na
tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na  –ty wyraz ciągu
–ty wyraz ciągu 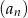 .
.
Dany jest nieskończony rosnący ciąg arytmetyczny 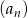 , dla
, dla 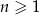 taki, że
taki, że 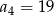 . Wyrazy
. Wyrazy 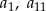 oraz
oraz 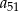 tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na
tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na  –ty wyraz ciągu
–ty wyraz ciągu 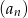 .
.
Pierwszy wyraz nieskończonego ciągu geometrycznego 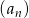 jest równy
jest równy 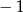 . Wyraz drugi, trzeci i czwarty spełniają warunek
. Wyraz drugi, trzeci i czwarty spełniają warunek 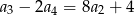 .
.
- Oblicz iloraz ciągu
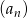 .
. - Określ, czy ciąg
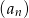 jest rosnący, czy malejący.
jest rosnący, czy malejący.
W ciągu arytmetycznym 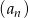 , określonym dla
, określonym dla 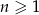 , dane są: wyraz
, dane są: wyraz 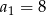 i suma trzech początkowych wyrazów tego ciągu
i suma trzech początkowych wyrazów tego ciągu 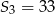 . Oblicz różnicę
. Oblicz różnicę 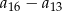 .
.
W ciągu arytmetycznym 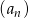 , określonym dla
, określonym dla 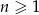 , dane są: wyraz
, dane są: wyraz 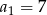 i suma czterech początkowych wyrazów tego ciągu
i suma czterech początkowych wyrazów tego ciągu 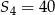 . Oblicz różnicę
. Oblicz różnicę 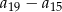 .
.
Liczby 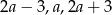 , w podanej kolejności, tworzą ciąg geometryczny. Wyznacz
, w podanej kolejności, tworzą ciąg geometryczny. Wyznacz  .
.
Trójwyrazowy ciąg 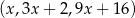 jest geometryczny. Oblicz
jest geometryczny. Oblicz  .
.
Dany jest trzywyrazowy ciąg 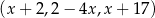 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Dany jest trzywyrazowy ciąg 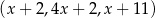 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Oblicz sumę szeregu
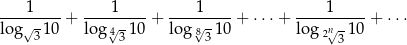
Oblicz granicę 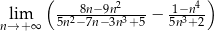 .
.
Dany jest nieskończony ciąg geometryczny 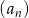 , który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym
, który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym 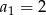 , oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu
, oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu 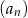 jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
Wyznacz zbiór wartości funkcji
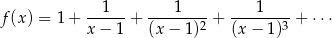
określonej dla wszystkich wartości  , dla których prawa strona powyższego wzoru jest sumą wyrazów zbieżnego szeregu geometrycznego.
, dla których prawa strona powyższego wzoru jest sumą wyrazów zbieżnego szeregu geometrycznego.
Ciąg 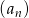 , gdzie
, gdzie 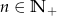 , określony jest następująco:
, określony jest następująco:
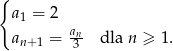
Wyznacz wszystkie wartości 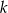 , dla których suma
, dla których suma 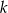 początkowych wyrazów ciągu
początkowych wyrazów ciągu 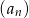 jest większa od
jest większa od 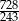 .
.
Ciąg 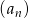 , gdzie
, gdzie 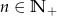 , określony jest następująco:
, określony jest następująco:
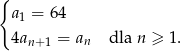
Wyznacz wszystkie wartości 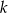 , dla których suma
, dla których suma 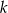 początkowych wyrazów ciągu
początkowych wyrazów ciągu 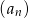 jest równa
jest równa 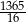 .
.
Znajdź  , dla którego liczby
, dla którego liczby 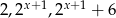 w podanej kolejności tworzą ciąg arytmetyczny.
w podanej kolejności tworzą ciąg arytmetyczny.
Nieskończony ciąg geometryczny 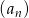 jest określony wzorem
jest określony wzorem 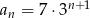 , dla
, dla 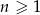 . Oblicz iloraz
. Oblicz iloraz 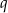 tego ciągu.
tego ciągu.
Nieskończony ciąg geometryczny 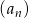 jest określony wzorem
jest określony wzorem 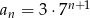 , dla
, dla 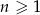 . Oblicz iloraz
. Oblicz iloraz 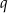 tego ciągu.
tego ciągu.
Nieskończony ciąg geometryczny 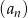 jest określony wzorem
jest określony wzorem 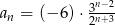 , dla
, dla 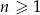 . Oblicz iloraz
. Oblicz iloraz 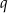 tego ciągu.
tego ciągu.
W ciągu arytmetycznym suma  początkowych wyrazów o numerach parzystych jest równa
początkowych wyrazów o numerach parzystych jest równa 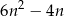 . Oblicz sumę
. Oblicz sumę  początkowych wyrazów o numerach nieparzystych.
początkowych wyrazów o numerach nieparzystych.
Pierwszy wyraz ciągu arytmetycznego 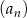 jest równy 4, a suma sześciu początkowych wyrazów tego ciągu wynosi 84.
jest równy 4, a suma sześciu początkowych wyrazów tego ciągu wynosi 84.
- Oblicz sumę pięćdziesięciu początkowych wyrazów tego ciągu.
- Dla jakiego
 liczby
liczby 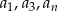 tworzą ciąg geometryczny?
tworzą ciąg geometryczny?
Pierwszy wyraz ciągu arytmetycznego 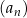 jest równy 2, a suma sześciu początkowych wyrazów tego ciągu wynosi 72.
jest równy 2, a suma sześciu początkowych wyrazów tego ciągu wynosi 72.
-
Oblicz sumę pięćdziesięciu początkowych wyrazów tego ciągu.
-
Dla jakiego
 liczby
liczby 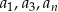 tworzą ciąg geometryczny?
tworzą ciąg geometryczny?
Dany jest ciąg 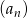 mający tę własność, że dla każdej liczby naturalnej
mający tę własność, że dla każdej liczby naturalnej  suma
suma  początkowych wyrazów tego ciągu jest równa
początkowych wyrazów tego ciągu jest równa 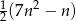 . Oblicz dwudziesty wyraz tego ciągu. Wykaż, że
. Oblicz dwudziesty wyraz tego ciągu. Wykaż, że 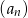 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Trzy liczby dodatnie 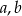 i
i  tworzą ciąg geometryczny. Suma tych liczb jest równa 26, a suma ich odwrotności wynosi
tworzą ciąg geometryczny. Suma tych liczb jest równa 26, a suma ich odwrotności wynosi 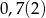 . Znajdź te liczby.
. Znajdź te liczby.
Niech 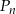 oznacza pole koła o promieniu
oznacza pole koła o promieniu 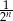 , dla
, dla 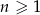 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 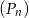 .
.
Niech 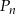 oznacza pole koła o promieniu
oznacza pole koła o promieniu 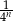 , dla
, dla 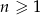 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 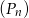 .
.
Niech 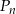 oznacza pole koła o promieniu
oznacza pole koła o promieniu 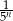 , dla
, dla 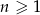 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 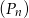 .
.
Niech 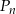 oznacza pole koła o promieniu
oznacza pole koła o promieniu 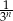 , dla
, dla 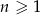 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 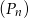 .
.
Suma  początkowych wyrazów ciągu geometrycznego
początkowych wyrazów ciągu geometrycznego 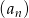 wyraża się wzorem
wyraża się wzorem 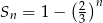 dla
dla 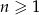 . Oblicz pierwszy wyraz ciągu i jego iloraz.
. Oblicz pierwszy wyraz ciągu i jego iloraz.

