Suma kątów wpisanego i środkowego opartych na tym samym łuku wynosi 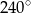 . Oblicz miarę kąta środkowego.
. Oblicz miarę kąta środkowego.
/Szkoła średnia/Geometria/Planimetria
Suma kątów wpisanego i środkowego opartych na tym samym łuku wynosi 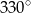 . Oblicz miarę kąta wpisanego.
. Oblicz miarę kąta wpisanego.
Oblicz pole rombu, którego jeden z kątów wewnętrznych wynosi 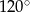 , a przekątna poprowadzona z wierzchołka tego kąta ma długość 10 cm.
, a przekątna poprowadzona z wierzchołka tego kąta ma długość 10 cm.
Krótsza przekątna rombu o długości 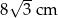 dzieli go na dwa trójkąty równoboczne. Oblicz pole rombu.
dzieli go na dwa trójkąty równoboczne. Oblicz pole rombu.
W trójkącie równoramiennym 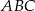 , w którym
, w którym  , wysokość poprowadzona z wierzchołka
, wysokość poprowadzona z wierzchołka 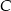 jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.
jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.
W trójkącie 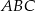 połączono środki boków i otrzymano trójkąt
połączono środki boków i otrzymano trójkąt 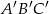 . Uzasadnij, że trójkąty
. Uzasadnij, że trójkąty 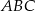 i
i 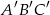 są podobne.
są podobne.
Punkty 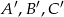 są środkami odpowiednio boków
są środkami odpowiednio boków 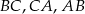 trójkąta
trójkąta 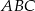 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 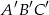 jest przystający do trójkąta
jest przystający do trójkąta 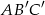 .
.
Trójkąty 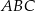 i
i 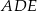 są równoboczne (zobacz rysunek). Punkty
są równoboczne (zobacz rysunek). Punkty 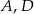 i
i 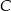 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 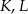 i
i 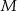 są środkami odcinków
są środkami odcinków 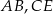 i
i 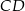 . Wykaż, że
. Wykaż, że 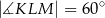 .
.
Podział odcinka, w wyniku którego otrzymujemy dwa odcinki takie, że stosunek długości krótszego z nich do długości dłuższego jest równy stosunkowi długości dłuższego odcinka do długości wyjściowego odcinka, nazywamy złotym podziałem odcinka.
- Odcinek
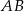 podzielono na dwa odcinki o długościach
podzielono na dwa odcinki o długościach 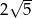 i
i 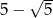 . Rozstrzygnij, czy dokonano złotego podziału odcinka
. Rozstrzygnij, czy dokonano złotego podziału odcinka  .
. - Dokonano złotego podziału odcinka o długości 2. Oblicz długości odcinków, na jakie podzielono dany odcinek.
Kąt przy podstawie trójkąta równoramiennego  ma miarę
ma miarę 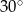 . Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta
. Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta 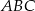 .
.
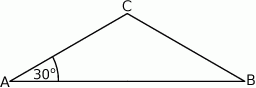
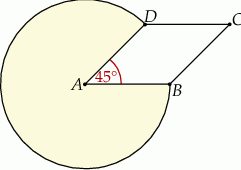
Oblicz pole wycinka koła o środku w punkcie 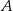 (zacieniowany obszar) jeśli pole rombu
(zacieniowany obszar) jeśli pole rombu 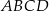 wynosi
wynosi 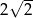 , a kąt ostry rombu ma miarę
, a kąt ostry rombu ma miarę 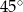 .
.
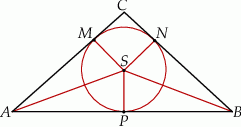
W trójkąt równoramienny 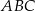 (
(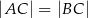 ) wpisano okrąg o środku
) wpisano okrąg o środku 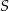 . Punkty wspólne okręgu i trójkąta oznaczono literami
. Punkty wspólne okręgu i trójkąta oznaczono literami 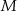 ,
, 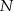 i
i 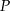 . Uzasadnij, że trójkąty
. Uzasadnij, że trójkąty 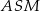 i
i 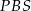 są przystające.
są przystające.
W kole o środku  poprowadzono cięciwę, która nie jest średnicą. Punkt
poprowadzono cięciwę, która nie jest średnicą. Punkt  dzieli tę cięciwę na dwa odcinki o długościach 11 i 29. Odcinek
dzieli tę cięciwę na dwa odcinki o długościach 11 i 29. Odcinek  ma długość 15. Oblicz promień tego koła.
ma długość 15. Oblicz promień tego koła.
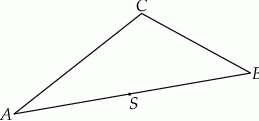
Dany jest trójkąt 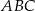 . Punkt
. Punkt 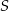 jest środkiem boku
jest środkiem boku 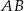 tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów
tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów 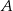 i
i 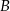 od prostej
od prostej 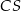 są równe.
są równe.
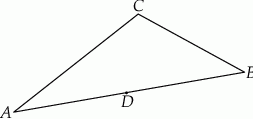
Na boku 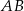 trójkąta
trójkąta 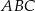 wybrano punkt
wybrano punkt  w ten sposób, że odległości punktów
w ten sposób, że odległości punktów 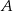 i
i  od prostej
od prostej 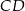 są równe (zobacz rysunek). Wykaż, że trójkąty
są równe (zobacz rysunek). Wykaż, że trójkąty 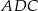 i
i 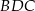 mają równe pola.
mają równe pola.
W trójkącie równoramiennym podstawa ma długość 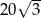 . Pole trójkąta jest równe
. Pole trójkąta jest równe 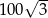 . Oblicz obwód tego trójkąta i miarę kąta przy podstawie.
. Oblicz obwód tego trójkąta i miarę kąta przy podstawie.
Oblicz sumę długości boków i pole trójkąta prostokątnego, w którym jedna z przyprostokątnych jest równa 10 cm, a druga jest o 2 cm krótsza od przeciwprostokątnej.
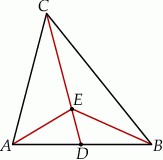
Na środkowej 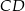 trójkąta
trójkąta 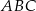 wybrano punkt
wybrano punkt 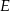 . Wykaż, że trójkąty
. Wykaż, że trójkąty 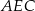 i
i 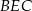 mają równe pola.
mają równe pola.
Oblicz sumę tangensów kątów ostrych trójkąta prostokątnego wiedząc że stosunek pola tego trójkąta do pola kwadratu, którego bokiem jest przeciwprostokątna danego trójkąta wynosi  .
.
Stosunek pola trójkąta prostokątnego do pola kwadratu, zbudowanego na przeciwprostokątnej tego trójkąta jest równy  . Oblicz sumę tangensów kątów ostrych tego trójkąta.
. Oblicz sumę tangensów kątów ostrych tego trójkąta.
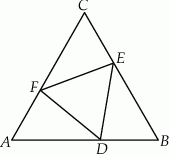
W trójkąt równoboczny 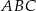 wpisano trójkąt
wpisano trójkąt 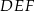 (patrz rysunek), tak że
(patrz rysunek), tak że 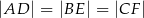 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 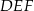 jest równoboczny.
jest równoboczny.
Przeciwprostokątna trójkąta prostokątnego ma długość 26 cm, a jedna z przyprostokątnych jest o 14 cm dłuższa od drugiej. Oblicz obwód tego trójkąta.
Przeciwprostokątna trójkąta prostokątnego ma długość 34 cm, a jedna z przyprostokątnych jest o 14 cm dłuższa od drugiej. Oblicz obwód tego trójkąta.
Oblicz wysokość i przekątną trapezu równoramiennego o podstawach 21 cm i 11 cm oraz ramieniu równym 13 cm.
Dany jest trójkąt ostrokątny równoramienny  , w którym bok
, w którym bok  jest równy
jest równy  . Odcinek
. Odcinek 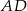 jest wysokością tego trójkąta, oraz odcinek
jest wysokością tego trójkąta, oraz odcinek 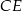 jest wysokością tego trójkąta. Udowodnij, że kąt
jest wysokością tego trójkąta. Udowodnij, że kąt 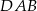 jest równy kątowi
jest równy kątowi 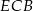 .
.
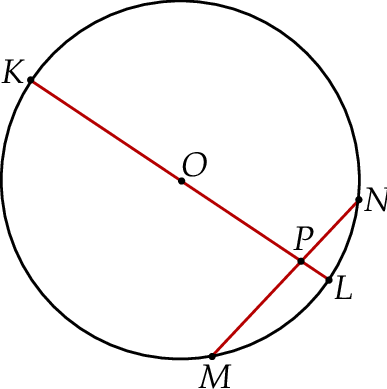
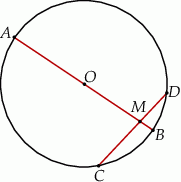
Cięciwa 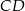 okręgu o środku
okręgu o środku 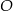 przecina średnicę
przecina średnicę 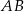 tego okręgu w punkcie
tego okręgu w punkcie 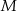 (rysunek). Kąt środkowy oparty na łuku
(rysunek). Kąt środkowy oparty na łuku 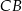 ma miarę
ma miarę 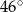 , a
, a 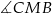 ma miarę
ma miarę 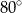 . Oblicz
. Oblicz 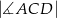 .
.
Cięciwa 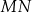 okręgu o środku
okręgu o środku 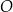 przecina średnicę
przecina średnicę 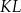 tego okręgu w punkcie
tego okręgu w punkcie 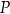 (rysunek). Kąt środkowy oparty na łuku
(rysunek). Kąt środkowy oparty na łuku 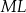 ma miarę
ma miarę 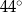 , a
, a 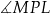 ma miarę
ma miarę 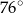 . Oblicz
. Oblicz 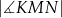 .
.