Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Prawdopodobieństwo/Z definicji

Wyszukiwanie zadań

Oblicz prawdopodobieństwo otrzymania dokładnie dwóch jedynek lub trzech szóstek w doświadczeniu losowym, polegającym na pięciokrotnym rzucie symetryczną sześcienną kostką do gry.

Do kina wybrało się 7 osób, wśród nich Basia i Janek. Wszyscy usiedli w jednym rzędzie, w którym jest dokładnie 7 wolnych miejsc. Oblicz, na ile sposobów wymienione osoby mogą zająć miejsca tak, by Basia i Janek siedzieli obok siebie. Oblicz też prawdopodobieństwo tego, że przy losowym zajmowaniu miejsc Basia i Janek nie siedzą obok siebie.

Oblicz prawdopodobieństwo tego, że przy czterokrotnym rzucie kostką, 3 kolejne wyniki utworzą ciąg geometryczny.

W pojemniku znajdują się dwie kule białe i trzy czerwone. Losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę czerwoną. Wynik przedstaw w postaci ułamka nieskracalnego.

Ukryj Podobne zadania

W pojemniku znajdują się dwie kule czerwone i trzy białe. Losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę czerwoną. Wynik przedstaw w postaci ułamka nieskracalnego.

W urnie znajdują się kule białe, zielone i czerwone. Kul zielonych jest dwa razy więcej niż kul białych, a kul czerwonych jest 3 razy więcej niż białych. Wyjęto dwa razy po jednej kuli bez zwracania. Oblicz liczbę kul białych w urnie, jeśli prawdopodobieństwo wylosowania dwóch kul zielonych jest równe 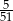-5 51 .

Na trzy półki kładziemy losowo 5 książek. Jakie jest prawdopodobieństwo tego, że jedna (i tylko jedna) z półek zostanie pusta?.

Rzucamy czterokrotnie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy dokładnie dwie dwójki lub dokładnie dwie piątki. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.

Ze zbioru liczb 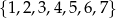{1,2,3 ,4 ,5,6,7} losujemy trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia 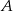A , polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 4.

20 drużyn rozdziela się losowo na 2 grupy po 10 drużyn. Oblicz prawdopodobieństwo tego, że 2 ustalone drużyny znajdą się w różnych grupach.

Ukryj Podobne zadania

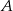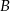Dziesięć osób rozdzielono na dwie drużyny po 5 osób. Oblicz prawdopodobieństwo, że osoby A i B będą w przeciwnych drużynach.

Ze zbioru liczb całkowitych spełniających nierówność 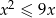2 x ≤ 9x losujemy dwie różne liczby. Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo wylosowania dwóch liczb pierwszych.

Z urny, w której znajduje się 20 kul białych i 2 czarne losujemy n kul. Znajdź najmniejszą wartość n , taką przy której prawdopodobieństwo wylosowania przynajmniej jednej kuli czarnej jest większe od 12 .

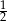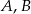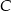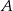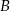Mamy 10 książek, wśród których są książki A ,B i C . Ustawiamy je losowo na pustej półce. Oblicz prawdopodobieństwo, że książki A i B będą stały obok siebie w dowolnym porządku, natomiast 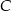C nie będzie sąsiadować z żadną z nich.

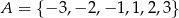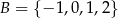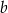Ze zbioru A = {− 3,− 2,− 1,1,2,3} losujemy liczbę a , natomiast ze zbioru B = {− 1,0,1 ,2} losujemy liczbę b . Te liczby są – odpowiednio – współczynnikiem kierunkowym i wyrazem wolnym funkcji liniowej 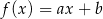f (x) = ax + b . Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymana funkcja 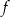f jest rosnąca i ma dodatnie miejsce zerowe.

Ukryj Podobne zadania

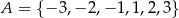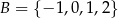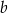Ze zbioru A = {− 3,− 2,− 1,1,2,3} losujemy liczbę a , natomiast ze zbioru B = {− 1,0,1 ,2} losujemy liczbę b . Te liczby są – odpowiednio – współczynnikiem kierunkowym i wyrazem wolnym funkcji liniowej 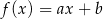f (x) = ax + b . Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymana funkcja 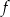f jest malejąca i ma dodatnie miejsce zerowe.

Rzucamy dwa razy symetryczną, sześcienną kostką, której jedna ściana ma jedno oczko, dwie ściany mają po dwa oczka i trzy ściany mają po trzy oczka. Oblicz prawdopodobieństwo zdarzenia: liczby oczek otrzymane w obu rzutach różnią się o 1.

Ze zbioru liczb 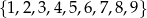{1,2,3,4 ,5,6,7,8,9} losujemy kolejno bez zwracania trzy liczby, zapisujemy je w kolejności losowania i tworzymy liczbę trzycyfrową w taki sposób, że pierwsza wylosowana liczba jest cyfrą setek, druga jest cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba trzycyfrowa jest podzielna przez 4. Wynik przedstaw w postaci ułamka nieskracalnego.

Dany jest ciąg 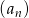(an) o wyrazie ogólnym 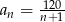-120- an = n+ 1 , dla każdej liczby naturalnej 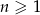n ≥ 1 . Ze zbioru liczb 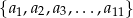{a1,a2,a3,...,a11} losujemy kolejno, trzy razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 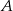A – wylosujemy trzy liczby całkowite, które będą kolejnymi wyrazami ciągu malejącego.

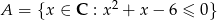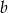Ze zbioru 2 A = {x ∈ C : x + x− 6 ≤ 0} losujemy 2 liczby a i b bez zwracania i tworzymy funkcję 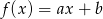f (x) = ax + b . Oblicz prawdopodobieństwo otrzymania funkcji malejącej.

Ukryj Podobne zadania

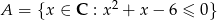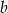Ze zbioru 2 A = {x ∈ C : x + x− 6 ≤ 0} losujemy 2 liczby a i b bez zwracania i tworzymy funkcję 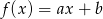f (x) = ax + b . Oblicz prawdopodobieństwo otrzymania funkcji, która nie ma miejsc zerowych.

Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 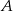A polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek w obu rzutach będzie podzielny przez 12. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.

Ukryj Podobne zadania

Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 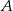A polegającego na tym, że w pierwszym rzucie otrzymamy nieparzystą liczbę oczek i suma liczb oczek w obu rzutach będzie większa od 6. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.

Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 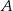A polegającego na tym, że iloczyn liczb oczek wyrzuconych w dwóch rzutach będzie podzielny przez 6.

Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 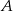A polegającego na tym, że w pierwszym rzucie otrzymamy nieparzystą liczbę oczek i iloczyn liczb oczek w obu rzutach będzie podzielny przez 6.

Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego do sześciu oczek. Niech 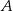A oznacza zdarzenie polegające na tym, że iloczyn liczb oczek wyrzuconych w dwóch rzutach jest równy 12. Oblicz prawdopodobieństwo zdarzenia A .

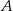Grupa 4 kobiet i 4 mężczyzn, w tym jedno małżeństwo, wybrała się na pieszą wycieczkę. Na wąskiej ścieżce musieli iść gęsiego tzn. jedno za drugim. Zakładamy, że wszystkie możliwe ustawienia tych osób są jednakowo prawdopodobne. Oblicz prawdopodobieństwo zdarzenia, że jako pierwsze pójdą kobiety i żona będzie szła bezpośrednio przed mężem. Sprawdź, czy to prawdopodobieństwo jest mniejsze od 0,001.

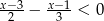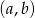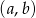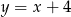Ze zbioru liczb naturalnych spełniających nierówność x−-3- x−1- 2 − 3 < 0 losujemy dwie różne liczby (a,b) . Oblicz prawdopodobieństwo zdarzenia: punkt o współrzędnych (a,b ) należy do wykresu funkcji y = x + 4 .

Strona 12 z 16