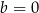Na płaszczyźnie, w kartezjańskim układzie współrzędnych  , dane są punkty
, dane są punkty 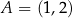 oraz
oraz 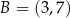 . Punkty
. Punkty 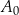 oraz
oraz 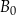 są odpowiednio obrazami punktów
są odpowiednio obrazami punktów 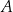 i
i 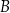 w symetrii środkowej o środku w punkcie
w symetrii środkowej o środku w punkcie 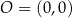 . Współczynnik kierunkowy prostej przechodzącej przez punkty
. Współczynnik kierunkowy prostej przechodzącej przez punkty 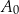 i
i 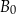 jest równy
jest równy
A)  B)
B) 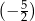 C)
C)  D)
D) 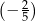
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Przekształcenia
Punkt 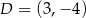 jest obrazem punktu
jest obrazem punktu 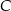 w symetrii względem punktu
w symetrii względem punktu 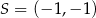 , a punkt
, a punkt 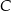 jest środkiem odcinka
jest środkiem odcinka 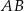 , gdzie
, gdzie 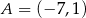 . Punkt
. Punkt 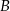 ma współrzędne
ma współrzędne
A) 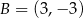 B)
B) 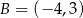 C)
C) 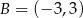 D)
D) 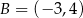
Punkt 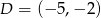 jest obrazem punktu
jest obrazem punktu  w symetrii względem punktu
w symetrii względem punktu  , a punkt
, a punkt 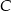 jest środkiem odcinka
jest środkiem odcinka 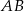 , gdzie
, gdzie 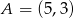 . Punkt
. Punkt 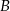 ma współrzędne
ma współrzędne
A) 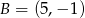 B)
B) 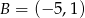 C)
C) 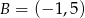 D)
D) 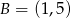
Dane są punkty 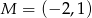 i
i 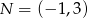 . Punkt
. Punkt 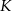 jest środkiem odcinka
jest środkiem odcinka 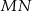 . Obrazem punktu
. Obrazem punktu 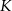 w symetrii względem początku układu współrzędnych jest punkt
w symetrii względem początku układu współrzędnych jest punkt
A) 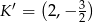 B)
B) 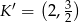 C)
C) 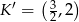 D)
D) 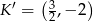
Dane są punkty 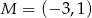 i
i 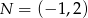 . Punkt
. Punkt 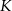 jest środkiem odcinka
jest środkiem odcinka 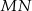 . Obrazem punktu
. Obrazem punktu 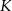 w symetrii względem początku układu współrzędnych jest punkt
w symetrii względem początku układu współrzędnych jest punkt
A) 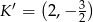 B)
B) 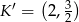 C)
C) 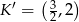 D)
D) 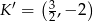
Punkt 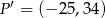 jest obrazem punktu
jest obrazem punktu 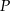 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 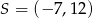 i skali
i skali 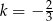 . Współrzędne punktu
. Współrzędne punktu 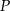 są równe
są równe
A) 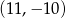 B)
B) 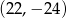 C)
C) 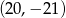 D)
D) 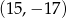
Punkt 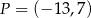 przekształcono w symetrii względem symetralnej odcinka o końcach
przekształcono w symetrii względem symetralnej odcinka o końcach 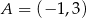 i
i 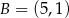 . W wyniku tego przekształcenia otrzymano punkt
. W wyniku tego przekształcenia otrzymano punkt 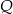 . Zatem długość odcinka
. Zatem długość odcinka 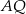 jest równa
jest równa
A) 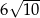 B)
B) 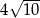 C)
C) 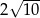 D)
D) 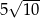
Punkt 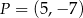 przekształcono w symetrii względem symetralnej odcinka o końcach
przekształcono w symetrii względem symetralnej odcinka o końcach 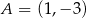 i
i 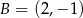 . W wyniku tego przekształcenia otrzymano punkt
. W wyniku tego przekształcenia otrzymano punkt 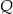 . Zatem długość odcinka
. Zatem długość odcinka 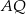 jest równa
jest równa
A) 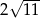 B)
B) 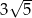 C)
C) 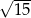 D)
D) 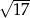
Punkty 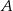 oraz
oraz 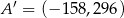 są symetryczne względem prostej
są symetryczne względem prostej 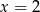 . Wówczas
. Wówczas
A) 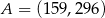 B)
B) 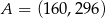 C)
C) 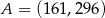 D)
D) 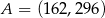
Punkty 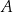 oraz
oraz 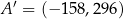 są symetryczne względem prostej
są symetryczne względem prostej 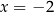 . Wówczas
. Wówczas
A) 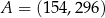 B)
B) 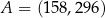 C)
C) 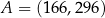 D)
D) 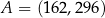
Punkty 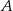 oraz
oraz 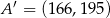 są symetryczne względem prostej
są symetryczne względem prostej 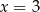 . Wówczas
. Wówczas
A) 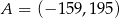 B)
B) 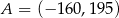 C)
C) 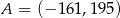 D)
D) 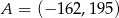
Punkt 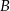 jest obrazem punktu
jest obrazem punktu 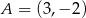 w symetrii względem początku układu współrzędnych, a punkt
w symetrii względem początku układu współrzędnych, a punkt 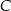 jest obrazem punktu
jest obrazem punktu 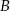 w symetrii względem punktu
w symetrii względem punktu 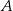 . Długość odcinka
. Długość odcinka 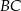 jest równa
jest równa
A) 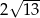 B)
B) 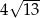 C)
C) 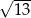 D)
D) 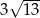
Obrazem punktu 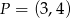 w symetrii środkowej względem punktu
w symetrii środkowej względem punktu 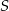 jest punkt
jest punkt 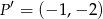 . Wynika stąd, że
. Wynika stąd, że
A) 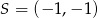 B)
B) 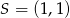 C)
C) 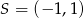 D)
D) 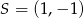
Punkt 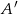 jest obrazem punktu
jest obrazem punktu 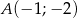 w symetrii względem prostej
w symetrii względem prostej 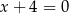 . Zatem
. Zatem
A) 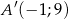 B)
B) 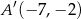 C)
C) 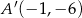 D)
D) 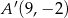
Punkt 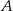 ma współrzędne
ma współrzędne 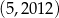 . Punkt
. Punkt 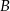 jest symetryczny do punktu
jest symetryczny do punktu 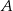 względem osi
względem osi 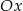 , a punkt
, a punkt 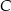 jest symetryczny do punktu
jest symetryczny do punktu 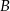 względem osi
względem osi 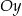 . Punkt
. Punkt 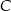 ma współrzędne
ma współrzędne
A) 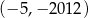 B)
B) 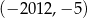 C)
C) 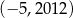 D)
D) 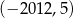
Punkt 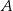 ma współrzędne
ma współrzędne 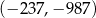 . Punkt
. Punkt 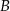 jest symetryczny do punktu
jest symetryczny do punktu 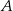 względem początku układu współrzędnych, a punkt
względem początku układu współrzędnych, a punkt 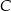 jest symetryczny do punktu
jest symetryczny do punktu 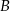 względem osi
względem osi 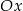 . Punkt
. Punkt 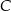 ma współrzędne
ma współrzędne
A) 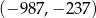 B)
B) 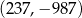 C)
C) 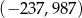 D)
D) 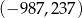
Punkt 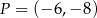 , przekształcono najpierw w symetrii względem osi
, przekształcono najpierw w symetrii względem osi 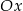 , a potem w symetrii względem osi
, a potem w symetrii względem osi 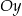 . W wyniku tych przekształceń otrzymano punkt
. W wyniku tych przekształceń otrzymano punkt 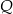 . Zatem
. Zatem
A) 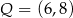 B)
B) 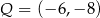 C)
C) 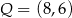 D)
D) 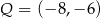
Punkt 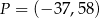 , przekształcono najpierw w symetrii względem osi
, przekształcono najpierw w symetrii względem osi 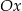 , a potem w symetrii względem osi
, a potem w symetrii względem osi 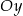 . W wyniku tych przekształceń otrzymano punkt
. W wyniku tych przekształceń otrzymano punkt 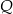 . Zatem
. Zatem
A) 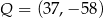 B)
B) 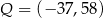 C)
C) 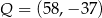 D)
D) 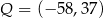
Punkt 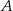 ma współrzędne
ma współrzędne 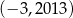 . Punkt
. Punkt 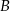 jest symetryczny do punktu
jest symetryczny do punktu 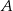 względem osi
względem osi 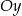 , a punkt
, a punkt 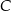 jest symetryczny do punktu
jest symetryczny do punktu 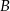 względem osi
względem osi 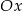 . Punkt
. Punkt 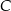 ma współrzędne
ma współrzędne
A) 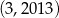 B)
B) 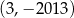 C)
C) 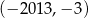 D)
D) 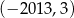
Odległość punktu 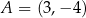 od jego obrazu w symetrii względem początku układu współrzędnych jest równa
od jego obrazu w symetrii względem początku układu współrzędnych jest równa
A) 6 B) 7 C) 8 D) 10
Punkt 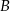 jest obrazem punktu
jest obrazem punktu 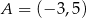 w symetrii względem początku układu współrzędnych. Długość odcinka
w symetrii względem początku układu współrzędnych. Długość odcinka 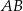 jest równa
jest równa
A) 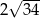 B) 8 C)
B) 8 C) 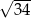 D) 12
D) 12
Punkt 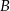 jest obrazem punktu
jest obrazem punktu 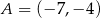 w symetrii względem początku układu współrzędnych. Długość odcinka
w symetrii względem początku układu współrzędnych. Długość odcinka 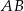 jest równa
jest równa
A) 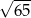 B)
B) 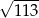 C)
C) 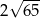 D) 13
D) 13
Punkt 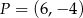 , przekształcono w symetrii względem prostej
, przekształcono w symetrii względem prostej 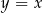 . W wyniku tego przekształcenia otrzymano punkt
. W wyniku tego przekształcenia otrzymano punkt 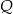 . Zatem
. Zatem
A) 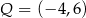 B)
B) 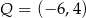 C)
C) 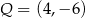 D)
D) 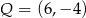
Punkt 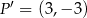 jest obrazem punktu
jest obrazem punktu 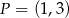 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 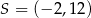 . Skala tej jednokładności jest równa
. Skala tej jednokładności jest równa
A)  B)
B)  C) 2 D) 3
C) 2 D) 3
Punkt 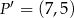 jest obrazem punktu
jest obrazem punktu 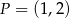 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 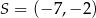 . Skala tej jednokładności jest równa
. Skala tej jednokładności jest równa
A) 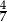 B)
B)  C) 3 D)
C) 3 D) 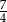
Punkt 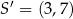 jest obrazem punktu
jest obrazem punktu 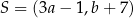 w symetrii osiowej względem osi
w symetrii osiowej względem osi 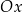 układu współrzędnych, gdy
układu współrzędnych, gdy
A) 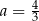 oraz
oraz 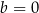 B)
B) 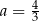 oraz
oraz 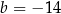
C) 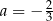 oraz
oraz 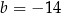 D)
D) 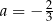 oraz
oraz